Материал к внеклассным занятиям по математике в 9-11 классах « Алгебраические методы решения прикладных задач на экстремум»

« Алгебраические методы решения прикладных задач на экстремум»
В технике и естествознании, как впрочем и в обыденной жизни
встречается особый вид задач. Это так называемые задачи на «максимум и минимум».
Люди издавна желали получить наибольшую выгоду при наименьших затратах. Такие задачи возникают там, где речь идет о том, как при разнообразных возможностях использования наличных средств добиться наилучшего эффекта. Эти задачи в математике называют задачами на экстремум. Огромное число таких задач возникает в экономике и технике.
В математике исследование задач на экстремум началось 25 веков назад. С возникновение математического анализа были созданы общие методы их решения.
Но и на сегодняшнем этапе оказалось, что методы решения этих задач не исчерпаны. Бурное развитие экономики и техники привело к новой теории- теории оптимального управления.

« Алгебраические методы решения прикладных задач на экстремум»
Метод, основанный на теореме о произведении 2-х множителей
Теорема1 Произведение двух множителей, сумма которых постоянна, имеет наибольшее значение при равенстве множителей.
max при
Примеры решения задач.
Окно имеет форму прямоугольника,
завершенного полукругом. При
заданном периметре найти размеры
окна, чтобы оно пропускало наибольшее
количество света.

Решение.
Пусть Х –высота окна до полукруга, Y –ширина, тогда R= Y/2. Р-const,
Откуда: ,
Функция S(x) имеет экстремум в тех же точках что и S(x)*(4+П). По теореме, если 4Р- const, то произведение
имеет наибольшее
значение при поэтому:
« Алгебраические методы решения прикладных задач на экстремум»

« Алгебраические методы решения прикладных задач на экстремум»
Пример решения задачи:
Из квадратного листа картона с заданной стороной нужно изготовить квадратную коробку, вырезая по углам листа равные квадраты и загибая образовавшиеся края. Какой величины должна быть сторона каждого вырезанного квадрата, чтобы объем сделанной коробки был наибольшим

Решение.
Пусть X – сторона вырезаемого квадрата
тогда объем коробки:
Величина Z = 4V достигает максимума при тех же значениях X, что и V
Имеем: По теореме имеем
произведение множителей, сумма которых
Значит максимума это произведение достигает при
откуда
« Алгебраические методы решения прикладных задач на экстремум»

« Алгебраические методы решения прикладных задач на экстремум»
Метод, основанный на теореме о произведении нескольких множителей.
Теорема2 Произведение нескольких положительных множителей, сумма которых постоянна, имеет наибольшее значение при равенстве множителей.
max при
Пример решения задачи.
Над центром круглого стола на блоке висит лампа. На какой высоте следует поместить эту лампу, чтобы на краях стола получить наибольшую освещенность?

« Алгебраические методы решения прикладных задач на экстремум»
Решение:
Сила света , где k – коэф-нт пропорц.
, где X- радиус стола. Имеем:
Величина
достигает максимума при тех же значениях, что и I.
Откуда
поэтому по теореме
наибольшее значение Z достигает, если:
то есть при , откуда . Значит .

Метод, основанный на теореме о сумме 2-х положительных слагаемых, произведение которых постоянно
Теорема3 Сумма двух положительных слагаемых, произведение которых постоянно имеет наименьшее значение при равных слагаемых
при
ПРИМЕР решения задачи.
Из всех равнобедренных треугольников данной площади, найти тот у которого сумма основания и медианы была бы наименьшей.
Решение: Пусть основание искомого треугольника 2Х, а медиана Y.
Тогда Сумма 2х+y достигает наименьшего
значения при 2x=y, т.к. 2хy=2S= const. Поэтому
« Алгебраические методы решения прикладных задач на экстремум»

« Алгебраические методы решения прикладных задач на экстремум»
Метод, основанный на теорема о сумме нескольких положительных слагаемых, произведение которых постоянно
Теорема4 Если сумма нескольких переменных X, Y, Z
постоянна, то произведение где p, q, r – данные положительные числа, имеет наибольшее значение, когда переменные пропорциональны своим показателям.
Пример решения задачи: Из квадратного листа картона с заданной стороной нужно изготовить квадратную коробку, вырезая по углам листа равные квадраты и загибая образовавшиеся края. Какой величины должна быть сторона каждого вырезанного квадрата, чтобы объем сделанной коробки был наименьшим.

Решение
Пусть X –сторона вырезаемого квадрата, тогда объем коробки:
Величина Z= 2V принимает максимум при тех же значениях, что и V. Имеем
Сумма
Значит по теореме имеем, что максимум
будет при условии
откуда
« Алгебраические методы решения прикладных задач на экстремум»

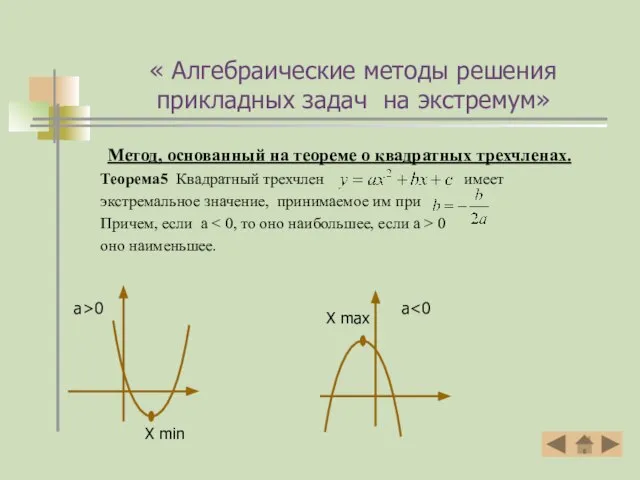
Метод, основанный на теореме о квадратных трехчленах.
Теорема5 Квадратный трехчлен имеет
экстремальное значение, принимаемое им при
Причем, если a < 0, то оно наибольшее, если а > 0
оно наименьшее.
« Алгебраические методы решения прикладных задач на экстремум»
X min
X max
a>0
a<0

ПРИМЕР решения задачи: В данный шар вписать цилиндр с наибольшей боковой поверхностью.
Решение: Пусть R- радиус шара, r- радиус основания
цилиндра, H – высота цилиндра. Боковая поверхность
цилиндра: По т. Пифагора
откуда:
Функция принимает наибольшее значение
при тех же значениях, что и S. Применяя теорему
имеем:
а высота:
« Алгебраические методы решения прикладных задач на экстремум»

« Алгебраические методы решения прикладных задач на экстремум»
Метод, основанный на теореме о среднем геометрическом положительных чисел.
Теорема6 Среднее геометрическое любого количества положительных чисел не больше их среднего арифметического.
Пример решения задачи: На вертикальной стене висит картина. На каком расстоянии от стены должен встать наблюдатель, чтобы угол под которым он видит картину оказался наибольшим?

« Алгебраические методы решения прикладных задач на экстремум»
Решение задачи: Пусть К- точка пересечения стены и горизонтальной прямой, проходящей через глаз наблюдателя. Тогда искомое расстояние есть ОК
Пусть Если углы КОА и КОВ обозначить через
то и
Т.к. То
Наибольшее значение угла будет достигаться
при наибольшем значении его тангенса. Значит
Дробь будет наибольшей, если
будет наименьшим, следовательно
B
A
K

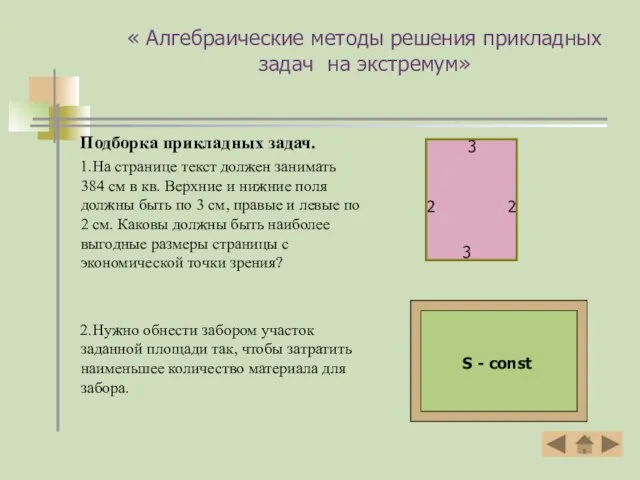
« Алгебраические методы решения прикладных задач на экстремум»
Подборка прикладных задач.
1.На странице текст должен занимать 384 см в кв. Верхние и нижние поля должны быть по 3 см, правые и левые по 2 см. Каковы должны быть наиболее выгодные размеры страницы с экономической точки зрения?
2.Нужно обнести забором участок заданной площади так, чтобы затратить наименьшее количество материала для забора.
S - const
3
3
2
2

« Алгебраические методы решения прикладных задач на экстремум»
Подборка прикладных задач.
4.Какие должны быть размеры треугольной песочницы, заданного периметра и высоты чтобы её вместимость была наибольшей?
3.Полоса жести заданной ширины должна быть согнута в виде открытого цилиндрического желоба (профиль желоба имеет форму кругового сегмента). Каким должен быть центральный угол, опирающийся на дугу этого сегмента, для того, чтобы вместимость желоба была наибольшей?

« Алгебраические методы решения прикладных задач на экстремум»
Подборка прикладных задач.
5.Длина почтовой посылки, сложенная с периметром поперечного сечения равна 60см.
Найти размеры посылки наибольшего объема, если она имеет форму:
А) параллелепипеда
Б) цилиндра
6.В данный шар вписать конус наибольшего объема

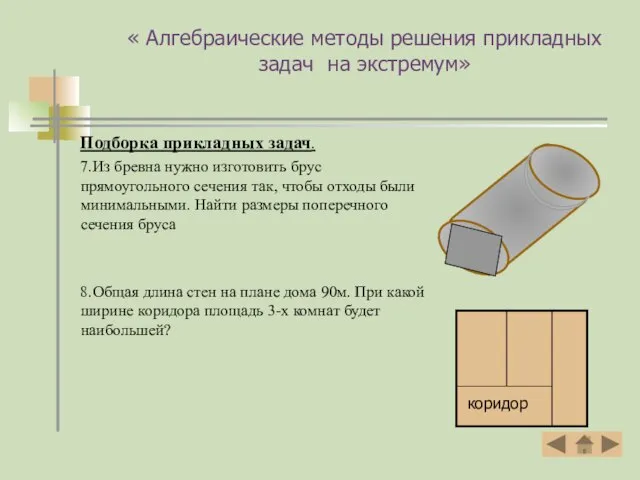
« Алгебраические методы решения прикладных задач на экстремум»
Подборка прикладных задач.
7.Из бревна нужно изготовить брус прямоугольного сечения так, чтобы отходы были минимальными. Найти размеры поперечного сечения бруса
8.Общая длина стен на плане дома 90м. При какой ширине коридора площадь 3-х комнат будет наибольшей?
коридор