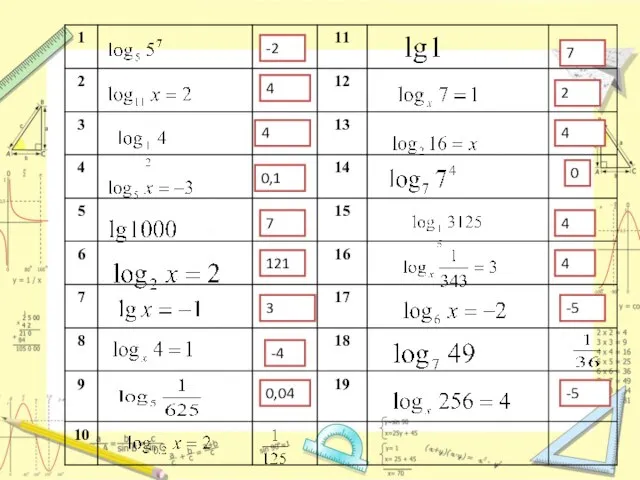
Слайд 37
121
0,04
4
0,1
3
-4
4
-2
0
-5
7
4
2
4
4
-5
Слайд 5Не является ни четной, ни нечетной;
Возрастает;
Не ограничена сверху, ограничена снизу
Не имеет наименьшего,
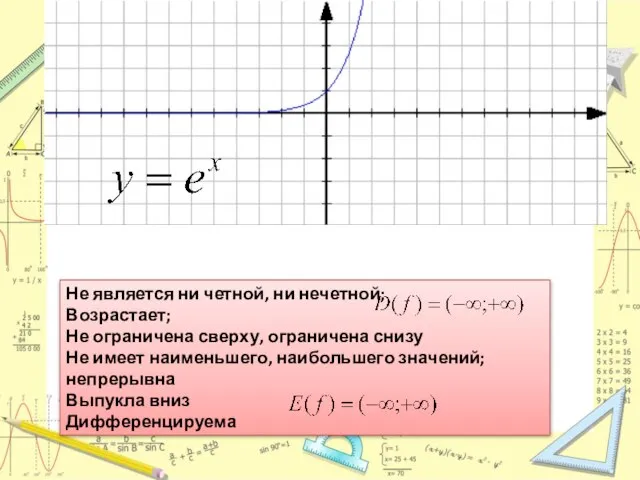
наибольшего значений; непрерывна
Выпукла вниз
Дифференцируема
Слайд 7-ctg x
tg x
cos x
-sin x
sin x
cos x
y=

f(kx+b)
y=f(x)+g(x)
Y=F(x)+G(x)
y=kf(x)
Y=kF(x)
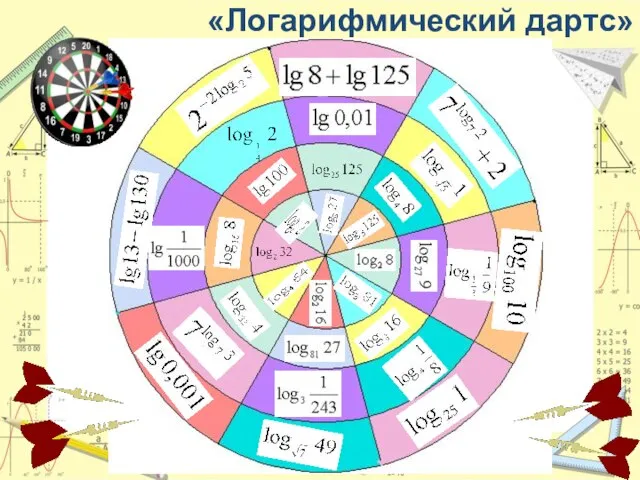
Слайд 10Логарифм по основанию е называется натуральным логарифмом
Десятичные логарифмы для наших потребностей являются

весьма удобными. Однако при изучении высшей математики более удобными оказываются логарифмы по основанию е = 2,718281828... (см. § 134, ч. 1). Употребление этих логарифмов позволяет значительно упростить большое количество математических формул. Логарифмы по основанию е получаются при решении многих физических задач и естественным образом входят в математическое описание некоторых химических, биологических и других процессов. Этим и объясняется их название «натуральные логарифмы».
Натуральный логарифм числа а обозначается ln а. Сейчас имеются достаточно полные таблицы натуральных логарифмов.
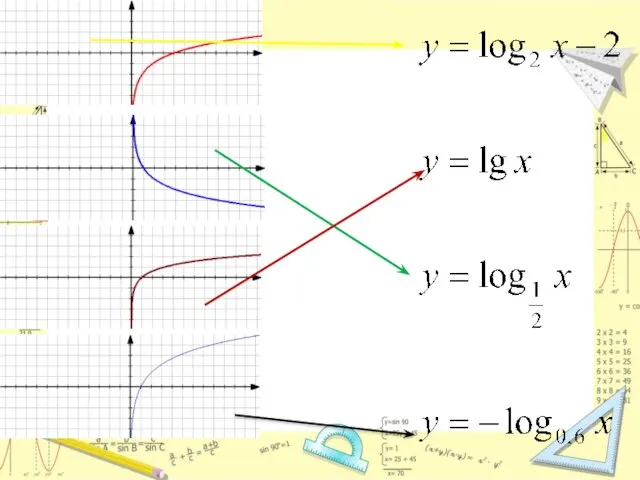
Слайд 12Функция вида y=lnx, свойства и график
Ни четна, ни нечетна
Не ограничена ни сверху,
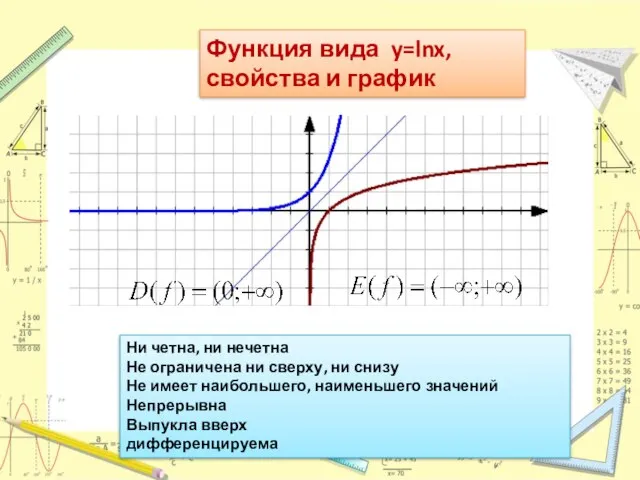
ни снизу
Не имеет наибольшего, наименьшего значений
Непрерывна
Выпукла вверх
дифференцируема
Слайд 141633, 1634, 1635, 1636(а,б)
Дома: в,г

Слайд 19Составить уравнение касательной к графику функции y=lnx в точке x=e
№1623,1637,1641 (а,б)
в,г -

дома
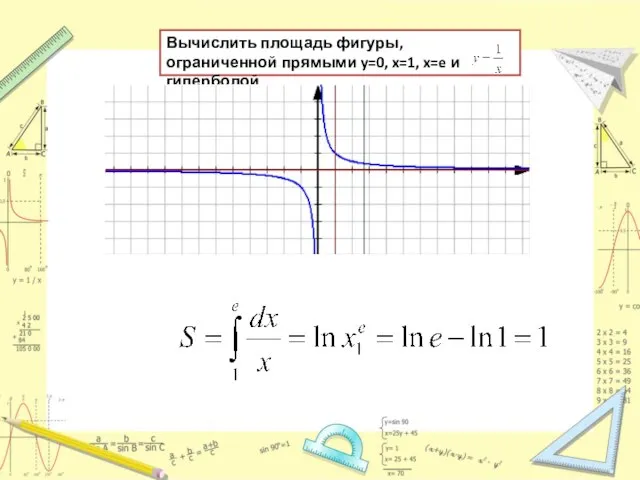
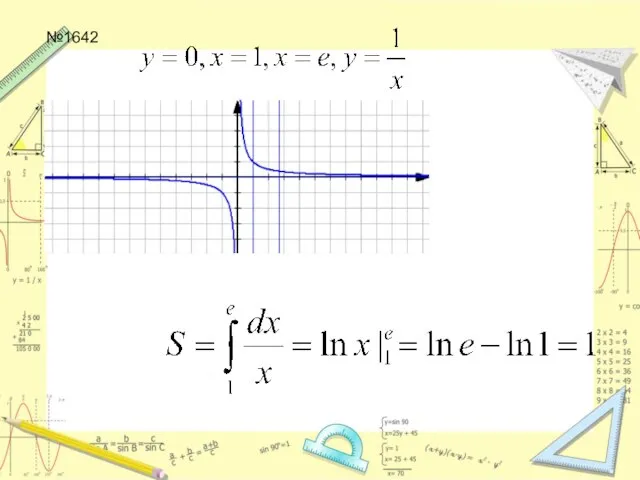
Слайд 21Вычислить площадь фигуры, ограниченной прямыми y=0, x=1, x=e и гиперболой
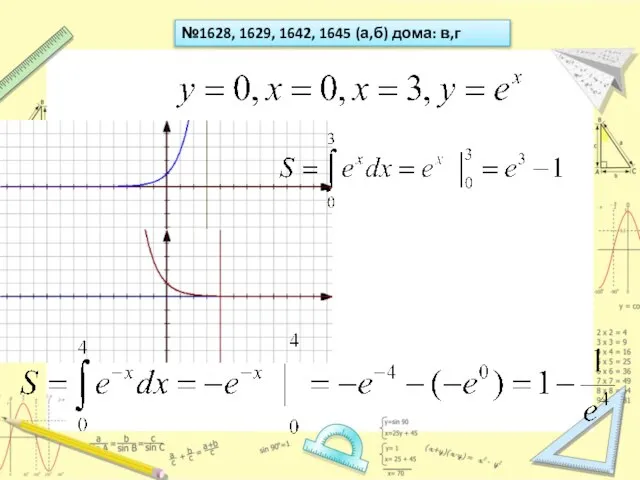
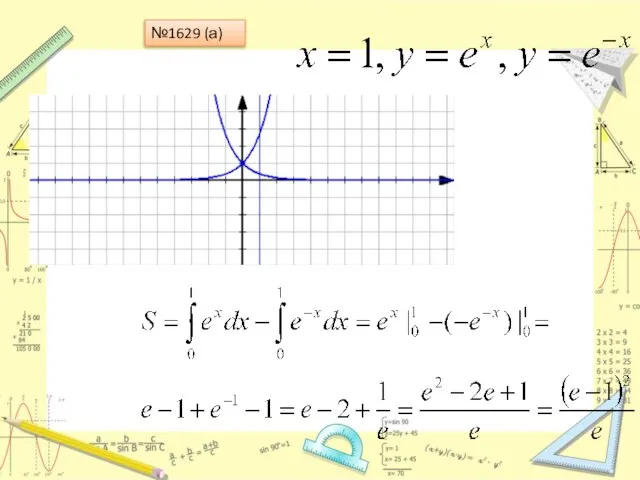
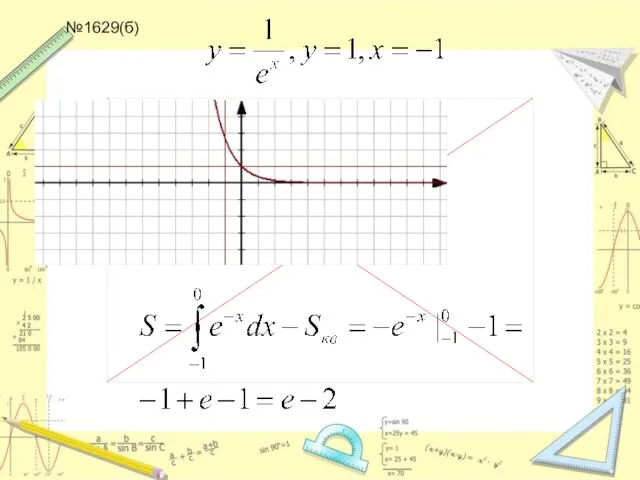
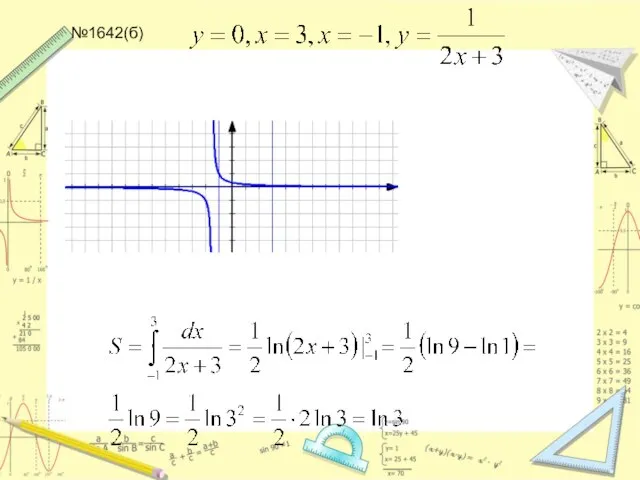
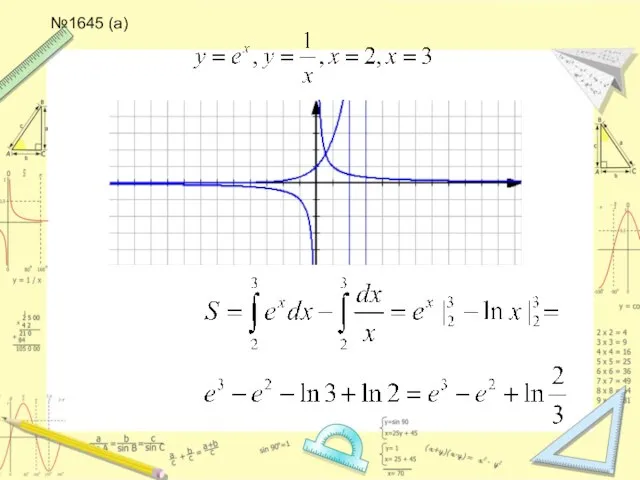
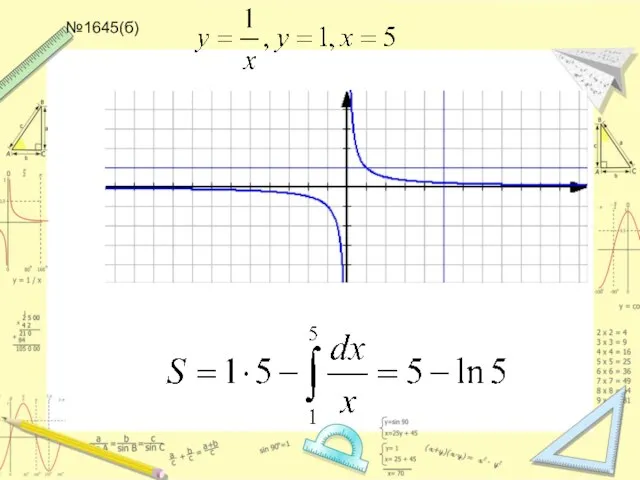
Слайд 22№1628, 1629, 1642, 1645 (а,б) дома: в,г







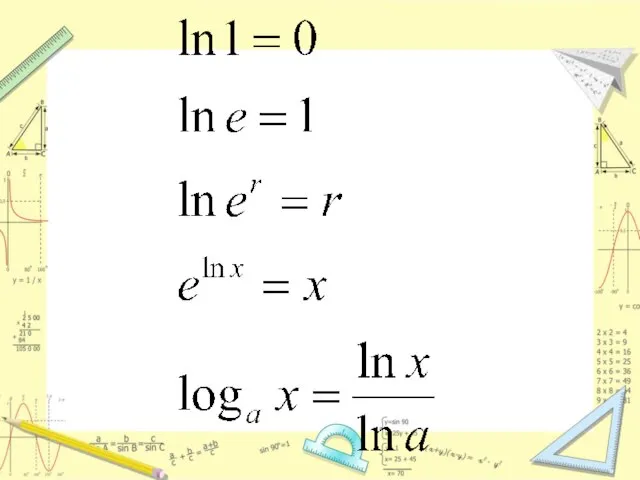

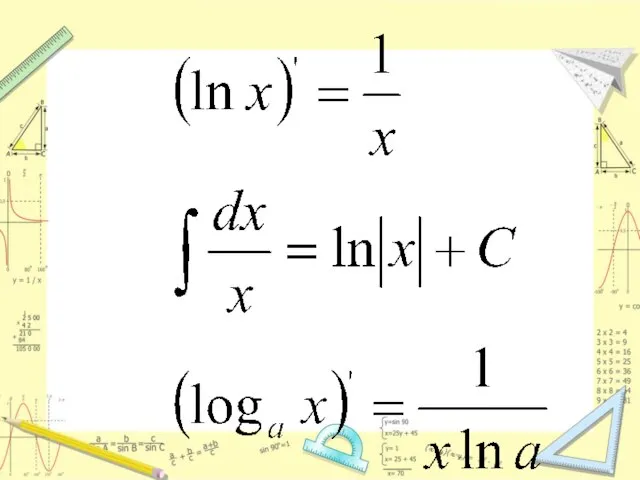









 Виды показательных уравнений
Виды показательных уравнений  Путешествие в страну дробных чисел
Путешествие в страну дробных чисел Задачи с параметрами. Тест. Создано учителем математики школы № 327 Марковой Н.А.
Задачи с параметрами. Тест. Создано учителем математики школы № 327 Марковой Н.А. Старая сказка на новый лад
Старая сказка на новый лад ТОЖДЕСТВА 7 класс
ТОЖДЕСТВА 7 класс  Заполните пропуски так, чтобы утверждения были верными - презентация по Алгебре_
Заполните пропуски так, чтобы утверждения были верными - презентация по Алгебре_ 9-klass-kvadratichnaya-funkciya.ppt
9-klass-kvadratichnaya-funkciya.ppt Метод рационализации
Метод рационализации Графическое решение систем уравнений
Графическое решение систем уравнений Презентация на тему Аварии на радиационно-опасных объектах
Презентация на тему Аварии на радиационно-опасных объектах  Сложение и вычитание смешанных чисел 5 класс
Сложение и вычитание смешанных чисел 5 класс Всё о квадратном уравнении
Всё о квадратном уравнении Презентация на тему ИСТОРИЧЕСКИЙ ПОРТРЕТ НИКОЛАЯ МИХАЙЛОВИЧА КАРАМЗИНА (1766
Презентация на тему ИСТОРИЧЕСКИЙ ПОРТРЕТ НИКОЛАЯ МИХАЙЛОВИЧА КАРАМЗИНА (1766 Квадратный трехчлен и его приложения
Квадратный трехчлен и его приложения Применение различных способов разложения на множители многочлена
Применение различных способов разложения на множители многочлена Алгебра модуля
Алгебра модуля Построение арифметических выражений
Построение арифметических выражений Uravneniya-s-parametrami.ppt
Uravneniya-s-parametrami.ppt Обратные тригонометрические функции
Обратные тригонометрические функции vzaimno-obratnye-funkcii.ppt
vzaimno-obratnye-funkcii.ppt Комбинаторные задачи Перестановки РазмещенияСочетания (выборки)
Комбинаторные задачи Перестановки РазмещенияСочетания (выборки) Арифметическая прогрессия.Формула n –го члена арифметической прогрессии
Арифметическая прогрессия.Формула n –го члена арифметической прогрессии Как появилось книгопечатание на Руси
Как появилось книгопечатание на Руси Свойства функций
Свойства функций Одночлены и многочлены 7 класс
Одночлены и многочлены 7 класс Презентация на тему Экзамен без стресса
Презентация на тему Экзамен без стресса  Методы решения логарифмических уравнений
Методы решения логарифмических уравнений Решение задач с помощью квадратных уравнений
Решение задач с помощью квадратных уравнений