Эконометрика. Отражение в спецификации эконометрической модели влияния на эндогенные переменные неучтённых факторов. Семинар 4

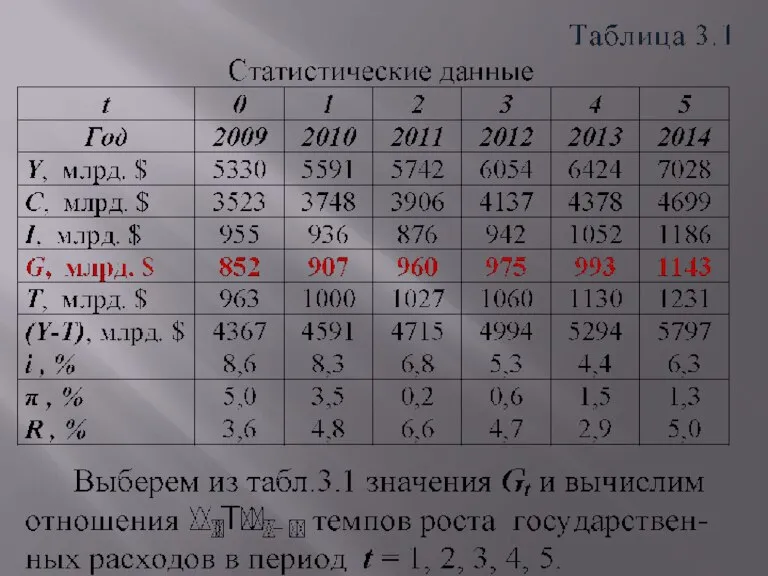
Задача 3.
1. Экономический объект – закрытая экономика.
2. Состояние объекта характеризуется следующими переменными:
Yt – валовый внутренний продукт (ВВП);
Сt – уровень потребления;
It – величина инвестиций;
Gt – государственные расходы.
3. Требуется составить спецификацию макромодели, позволяющей объяснить текущие эндогенные переменные:
Yt , Ct , It , Gt
их лаговыми значениями.

Экономические утверждения:
а) текущее потребление объясняется уровнем ВВП в предыдущем периоде, возрастая вместе с ним, но с меньшей скоростью:
b) величина инвестиций прямо пропорциональна приросту ВВП за предшествующий период (прирост ВВП за предшествующий период: Yt-1−Yt-2):
c) государственные расходы возрастают с постоянным темпом роста:

d) текущее значение ВВП есть сумма текущих уровней потребления, инвестиций и государственных расходов (тождество системы национальных счетов):
Т.о. спецификация модели делового цикла экономики в структурной форме (предложена лауреатами Нобелевской премии Самуэльсоном и Хиксом):
(3.4)

Модель (3.4) состоит из трёх поведенческих уравнений (1-е, 2-е и 3-е уравнения) и одного тождества. Она очень близка к приведённой форме:
текущие переменные Ct , It , Gt – явные функции предопределённых переменных Yt-1 , Yt-2 , Gt-1.
Если подставить правые части первых 3-х уравнений модели (3.4) в правую часть 4-го уравнения, то получим приведённую форму модели Самуэльсона – Хикса:
(3.5)

Спецификации (3.4 и 3.5) содержат четыре неизвестных параметра a0, a1, b, g.
Требуется:
a) при помощи реальных данных (табл.3.1) показать, что на текущие эндогенные пере-менные Yt , Ct , It , Gt моделей (3.4 и 3.5) оказывают влияние не только предопреде-лённые переменные Yt-1 , Yt-2 , Gt-1 этих моделей, но также и другие факторы, которые не определены;
b) уточнить спецификацию модели (3.4) путём включения в неё случайных возмущений.

Из спецификации (3.4) модели Самуэльсона – Хикса (3-е уравнение) следует, что
Если (3.6) несправедливо, то это будет дока-зательством воздействия на текущие эндогенные переменные факторов, неучтённых в рамках модели (3.4).

В результате убеждаемся – выражение (3.6) не выполняется. Это доказывает то, что на переменную Gt влияют какие-то факторы, не отражённые в модели (3.4). Более того, отношение от периода к периоду хаотично колеблется. Это даёт основание интерпретировать влияние неидентифицированных (неустановленных) факторов как случайное.
Можно ли это учесть?
Да, можно! Причём по-разному.

Например, заменить 3-е уравнение модели (3.4) тремя следующими уравнениями:
В первом уравнении системы (3.7) случайная величина wt отражает влияние на текущую эндогенную переменную Gt не определённых в модели факторов.
Во втором уравнении спецификации (3.7) постулируется, что при каждом фиксированном значении Gt-1 случайное возмущение wt имеет нулевое ожидаемое значение.

Третье уравнение спецификации (3.7) отражает жёсткое предположение – средний квадрат разброса значений wt вокруг нуля сохраняется неизменным (хотя и неизвестным) при любом фиксированном значении предопределённой переменной Gt-1 .
В эконометрике случайные возмущения с таким свойством именуются
гомоскедастичными.

Гипотеза о гомоскедастичности возмущения заложенная в 3-м уравнении системы (3.7), может и не соответствовать реальности. Тогда её можно отбросить и заменить, например, такой предпосылкой:
где λ – некоторое действительное число,
σ0 – некоторое положительное число.
Модель (3.8) означает, что средний квадрат разброса значений wt вокруг нуля является степенной функцией уровня государственных расходов Gt-1 в предыдущем периоде.
(3.8)

Случайное возмущение wt является
гетероскедастичным,
если величина
зависит от уровня объясняющей переменной Gt-1.
Выражение (3.8) – это простейшая модель гетероскедастичности случайного остатка.

Таким образом, второй возможный вариант отражения в спецификации модели Самуэльсона – Хикса влияния на переменную Gt неопределённых факторов имеет вид:
Для определённости остановимся пока на спецификации (3.7), которую будем называть эконометрической моделью Самуэльсона – Хикса государственных расходов.

Слагаемое в правой части 1-го уравнения системы (3.7) именуется
функцией регрессии.
Функция регрессии отражает влияние на те-кущую эндогенную переменную предопределёных переменных модели.
Аналогичные рассуждения приводят к следующей спецификации эконометрической модели Самуэльсона – Хикса делового цикла экономики: