Конъюнкция. Логика высказываний

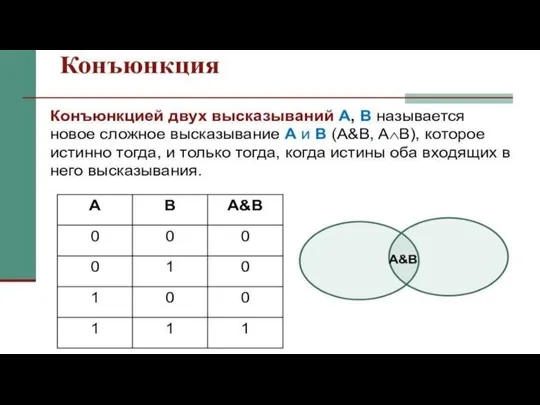
КОНЪЮНКЦИЯ
(от латинского conjunctio - союз, связь.)
Если два высказывания соединены союзом И, то полученное сложное высказывание обычно считается истинным тогда и только тогда, когда истинны оба составляющие его высказывания. Если хотя бы одно из составляющих высказываний ложно, то и полученное из них с помощью союза «И» сложное высказывание также считается ложным.

Например, возьмем два высказывания:
"У кота есть хвост" (А) "У зайца есть хвост" (В)
Сложное высказывание "У кота есть хвост и у зайца есть хвост" истинно, т.к. истинны оба высказывания А и В.

Но если взять другие высказывания:
"У кота длинный хвост" (С) "У зайца длинный хвост" (D)
то сложное высказывание "У кота длинный хвост и у зайца длинный хвост“ будет ложным, т.к. ложно высказывание (D).

a & b, a ∧ b, a*b, a AND b
По аналогии с умножением в алгебре знак логического умножения может быть пропущен: ab.
Конъюнкция может быть бинарной операцией, то есть, иметь два операнда, тернарной операцией, т.е. иметь три операнда или n-арной операцией, т.е. иметь n операндов. Чаще всего встречаются следующие варианты инфиксной записи:

Связь с естественным языком
Часто указывают на сходство между конъюнкцией и союзом "и" в естественном языке. Составное утверждение "A и B" считается истинным, когда истинны оба утверждения A и B, в противном случае составное утверждение ложно.

Связь с булевой математикой
Это в точности соответствует определению конъюнкции в булевой алгебре, если "истину" обозначать как 1, а "ложь" как 0. При этом часто делают стандартную оговорку о неоднозначности естественного языка.

Например, в зависимости от контекста союз "и" может нести дополнительный оттенок "и тогда", "и поэтому", "и потом"..."И" также несет в себе оттенок неопределенного смысла.

Отличие логики естественного языка от математической остроумно выразил американский математик Стивен Клини, заметив, что в естественном языке "Мэри вышла замуж и родила ребенка" — не то же самое, что "Мэри родила ребенка и вышла замуж".

Соединительная связка представлена в сложном субъекте по схеме: S1 и S2 есть Р. Например: «Конфискация имущества и лишение звания являются дополнительными уголовно-правовыми санкциями».
В языке соединительное суждение может быть выражено одной из трех логико-грамматических структур:

Связка представлена в сложном предикате по схеме: S есть P1 и P2. Например: «Преступление — это общественно опасное и противоправное деяние».

Связка представлена сочетанием первых двух способов по схеме: S1 и S2 есть Р1 и Р2. Например:
«С полицмейстером и прокурором Ноздрев тоже был на «ты» и обращался по-дружески» (Н.В. Гоголь).

Список литературы:
Кириллов В.И., Старченко А.А. Логика. М.: Проспект, 2013
Логика: учебник для бакалавров / под ред. Л.А. Деминой. М.: Проспект, 2013
Хоменко И.В. Логика. Теория и практика аргументации. М., 2011
Ивин А.А. Теория аргументации. М., 2010