Логика. Суждение (Тема №3)

План лекции:
Суждение как форма мышления.
Виды суждений.
Простые суждения.
Логический квадрат.
Сложные суждения.

1.
Суждение (высказывание) – это форма мышления, в которой что-либо утверждается или отрицается.
Например: «Все сосны являются деревьями», «Некоторые люди – это спортсмены», «Ни один кит – не рыба», «Некоторые животные не являются хищниками».

Можно выделить несколько важных свойств суждения, которые отличают его от понятия:
1. Любое суждение состоит из понятий, связанных между собой.
Например, если связать понятия «карась » и «рыба », то могут получиться суждения: «Все караси являются рыбами», «Некоторые рыбы являются карасями» .

2. Любое суждение выражается в форме повествовательного предложения, риторического вопроса или риторического восклицания (вспомним, понятие выражается словом или словосочетанием). Например, в высказывании: «Попробуй найти чёрную кошку в тёмной комнате, если её там нет! » – в форме восклицательного предложения утверждается мысль о невозможности предложенного действия, в силу чего данное восклицание выражает собой суждение.

3. Любое суждение является истинным или ложным. Если суждение соответствует действительности, оно истинное, а если не соответствует – ложное. Например, суждение: «Все розы – это цветы», – является истинным, а суждение: «Все мухи – это птицы», – ложным.

Понятия, в отличие от суждений, не могут быть истинными или ложными. Понятие – это форма мышления, которая обозначает какой-либо объект, – и именно поэтому не может быть истинным или ложным.
Истинность или ложность – это всегда характеристика какого-то высказывания, утверждения или отрицания, поэтому она применима только к суждениям, но не к понятиям.
Поскольку любое суждение принимает одно из двух значений – истины или лжи – то аристотелевская логика также часто называется двузначной логикой.

4. Суждения бывают простыми и сложными. Сложные суждения состоят из простых, соединённых каким-либо союзом.
Как видим, суждение – это более сложная форма мышления по сравнению с понятием.

Суждение имеет определённую структуру, в которой можно выделить четыре части:
1. Субъект (обозначается латинской буквой S) – это то, о чём идёт речь в суждении. Например, в суждении: «Все учебники являются книгами», – речь идёт об учебниках, поэтому субъектом данного суждения выступает понятие «учебники».

2. Предикат (обозначается латинской буквой Р) – это то, что говорится о субъекте. Например, в том же суждении: «Все учебники являются книгами», – о субъекте (об учебниках) говорится, что они – книги, поэтому предикатом данного суждения выступает понятие «книги».

3. Связка – это то, что соединяет субъект и предикат. В роли связки могут быть слова «есть», «является», «это» и т. п.
4. Квантор – это указатель на объём субъекта. В роли квантора могут быть слова «все», «некоторые», «ни один» и т. п.

Если в каком-то суждении отсутствует связка или квантор, то они всё равно подразумеваются. С помощью условных обозначений субъекта и предиката можно отбросить содержание суждения и оставить только его логическую форму.

Субъект и предикат любого суждения всегда представляют собой какие-либо понятия, которые, как мы уже знаем, могут находиться в различных отношениях между собой. Между субъектом и предикатом суждения могут быть следующие отношения.
Равнозначность. В суждении: «Все квадраты – это равносторонние прямоугольники», – субъект «квадраты» и предикат «равносторонние прямоугольники» находятся в отношении равнозначности, потому что представляют собой равнозначные понятия (квадрат – это обязательно равносторонний прямоугольник, а равносторонний прямоугольник – это обязательно квадрат).S = P.

2. Пересечение. В суждении: «Некоторые писатели – это американцы», – субъект «писатели » и предикат «американцы » находятся в отношении пересечения, т. к. являются пересекающимися понятиями (писатель может быть американцем и может им не быть, и американец может быть писателем, но также может им не быть). Некоторые S это Р.

3. Подчинение (между субъектом и предикатом суждения возможны два варианта отношений: объём субъекта полностью включается в объём предиката, или наоборот).
В суждении: «Все тигры – это хищники», – субъект «тигры» и предикат «хищник » находятся в отношении подчинения, потому что представляют собой видовое и родовое понятия (тигр – это обязательно хищник, но хищник не обязательно тигр).
«Некоторые хищники являются тиграми», – субъект «хищники» и предикат «тигры» также находятся в отношении подчинения.

4. Несовместимость. В суждении: «Все планеты не являются звёздами», – субъект «планеты» и предикат «звёзды» находятся в отношении несовместимости, т. к. являются несовместимыми (соподчинёнными) понятиями (ни одна планета не может быть звездой, и ни одна звезда не может быть планетой).

Все суждения подразделяют на три вида:
1. Атрибутивные суждения (от лат. attributum – атрибут) – это суждения, в которых предикат представляет собой какой-либо существенный, неотъемлемый признак субъекта. Например, суждение: «Все воробьи – это птицы», – атрибутивное, потому что его предикат является неотъемлемым признаком субъекта: быть птицей – это главный признак воробья, его атрибут, без которого он не будет самим собой (если некий объект не птица, то он обязательно и не воробей).

В атрибутивном суждении не обязательно предикат является атрибутом субъекта, может быть и наоборот – субъект представляет собой атрибут предиката.
Например, в суждении: «Некоторые птицы – это воробьи» (как видим, по сравнению с вышеприведённым примером, субъект и предикат поменялись местами), субъект является неотъемлемым признаком (атрибутом) предиката.
Однако эти суждения всегда можно формально изменить таким образом, что предикат станет атрибутом субъекта. Поэтому атрибутивными обычно называются те суждения, в которых предикат является атрибутом субъекта.

2. Экзистенциальные суждения (от лат. existentia – существование) – это суждения, в которых предикат указывает на существование или несуществование субъекта.
Например, суждение: «Вечных двигателей не бывает», – является экзистенциальным, т. к. его предикат «не бывает» свидетельствует о несуществовании субъекта (вернее – предмета, который обозначен субъектом).

3. Релятивные суждения (от лат. relativus – относительный) – это суждения, в которых предикат выражает собой какое-то отношение к субъекту. Например, суждение: «Москва основана раньше Санкт-Петербурга»,– является релятивным, потому что его предикат «основана раньше Санкт-Петербурга» указывает на временное (возрастное) отношение одного города и соответствующего понятия к другому городу и соответствующему понятию, представляющему собой субъект суждения.

2.
Если в суждении присутствуют один субъект и один предикат, то оно является простым. Все простые суждения по объёму субъекта и качеству связки делятся на четыре вида.
Объём субъекта может быть общим («все») и частным («некоторые»), а связка может быть утвердительной («есть») и отрицательной («не есть»):
Объём субъекта ……………… «все» «некоторые»
Качество связки ……………… «есть» «не есть».

Каждый из этих видов имеет своё название и условное обозначение:
1. Общеутвердительные суждения (обозначаются латинской буквой A) – это суждения с общим объёмом субъекта и утвердительной связкой: «Все S есть Р». Например: «Все школьники являются учащимися».
2. Частноутвердительные суждения (обозначаются латинской буквой I) – это суждения с частным объёмом субъекта и утвердительной связкой: «Некоторые S есть Р». Например: «Некоторые животные являются хищниками».

3. Общеотрицательные суждения (обозначаются латинской буквой E) – это суждения с общим объёмом субъекта и отрицательной связкой: «Все S не есть Р (или «Ни одно S не есть Р »). Например: «Все планеты не являются звёздами», «Ни одна планета не является звездой».
4. Частноотрицательные суждения (обозначаются латинской буквой O) – это суждения с частным объёмом субъекта и отрицательной связкой: «Некоторые S не есть Р». Например: «Некоторые грибы не являются съедобными».

Распределённые и нераспределённые термины
Терминами суждения называются его субъект и предикат.
Термин считается распределённым (развёрнутым, исчерпанным, взятым в полном объёме), если в суждении речь идёт обо всех объектах, входящих в объём этого термина. Распределённый термин обозначается знаком «+», а на схемах Эйлера изображается полным кругом (кругом, который не содержит в себе другого круга и не пересекается с другим кругом). Например, в суждении: «Все акулы (S) являются хищниками (Р)», – речь идёт обо всех акулах, значит, субъект этого суждения распределён. (S+)

Термин считается нераспределённым (неразвёрнутым, неисчерпанным, взятым не в полном объёме), если в суждении речь идёт не обо всех объектах, входящих в объём этого термина.
Нераспределённый термин обозначается знаком «–», а на схемах Эйлера изображается неполным кругом (кругом, который содержит в себе другой круг или пересекается с другим кругом).

Проще всего устанавливать распределённость терминов в простых суждениях с помощью схем Эйлера (полный круг соответствует распределённому термину, а неполный – нераспределённому).
В суждении: «Некоторые русские писатели – это всемирно известные люди». Сначала найдём в этом суждении субъект и предикат: «русские писатели» – субъект, «всемирно известные люди» – предикат.
Теперь установим, в каком они отношении. Русский писатель может, как быть, так и не быть всемирно известным человеком, и всемирно известный человек может, как быть, так и не быть русским писателем, следовательно, субъект и предикат указанного суждения находятся в отношении пересечения.

И субъект, и предикат изображаются неполными кругами (у каждого из них как бы отрезана какая-то часть), следовательно, оба термина предложенного суждения нераспределены (S –, P –).
«Некоторые люди – это спортсмены». Найдя в этом суждении субъект и предикат: «люди» – субъект, «спортсмены» – предикат, и установив отношение между ними – подчинение, изобразим его на схеме Эйлера, заштриховав ту часть, о которой идёт речь в суждении.
Круг, обозначающий предикат, является полным, а круг, соответствующий субъекту, – неполным (круг предиката как бы вырезает из него какую-то часть). Таким образом, в данном суждении субъект нераспределён, а предикат распределён (S –, P +).

Существует три способа преобразования простых суждений: обращение, превращение и противопоставление предикату.
1. Обращение (конверсия) – это преобразование простого суждения, при котором субъект и предикат меняются местами. Например, суждение: «Все акулы являются рыбами», – преобразуется путём обращения в суждение: «Некоторые рыбы являются акулами».

Обратим внимание на то, что в рассмотренном выше примере исходное суждение было вида A , а новое – вида I , т. е. операция обращения привела к смене вида простого суждения. При этом, конечно же, поменялась его форма, но не поменялось содержание, ведь в суждениях:
«Все акулы являются рыбами» и «Некоторые рыбы являются акулами», – речь идёт об одном и том же.

2. Превращение (обверсия), заключается в том, что у суждения меняется связка: положительная на отрицательную, или наоборот. При этом предикат суждения заменяется противоречащим понятием (т. е. перед предикатом ставится частица «не»). Например, то же самое суждение, которое мы рассматривали в качестве примера для обращения: «Все акулы являются рыбами», – преобразуется путём превращения в суждение: «Все акулы не являются не рыбами».

Приведённый пример превращения демонстрирует важную логическую закономерность: любое утверждение равно двойному отрицанию, и наоборот. Как видим, исходное суждение вида A в результате превращения стало суждением вида E.

3. Противопоставление предикату – состоит в том, что сначала суждение подвергается превращению, а потом обращению.
Например, чтобы путём противопоставления предикату преобразовать суждение: «Все акулы являются рыбами», – надо сначала подвергнуть его превращению. Получится: «Все акулы не являются не рыбами».
Теперь надо совершить обращение с получившимся суждением, т. е. поменять местами его субъект «акулы» и предикат «не рыбы». После этого совершим обращение с суждением: «Все акулы не являются не рыбами». Получится: «Все не рыбы не являются акулами».

4.
Простые суждения делятся на сравнимые и несравнимые.
Сравнимые (идентичные по материалу) суждения имеют одинаковые субъекты и предикаты, но могут отличаться кванторами и связками.
Например, суждения: «Все школьники изучают математику», «Некоторые школьники не изучают математику», – являются сравнимыми: у них совпадают субъекты и предикаты, а кванторы и связки различаются.

Несравнимые суждения имеют разные субъекты и предикаты. Например, суждения: «Все школьники изучают математику», «Некоторые спортсмены – это олимпийские чемпионы», – являются несравнимыми: субъекты и предикаты у них не совпадают.

Сравнимые суждения бывают, как и понятия, совместимыми и несовместимыми и могут находиться в различных отношениях между собой.
Совместимыми называются суждения, которые могут быть одновременно истинными. Например, суждения: «Некоторые люди – это спортсмены», «Некоторые люди – это не спортсмены», – являются одновременно истинными и представляют собой совместимые суждения.

Несовместимыми называются суждения, которые не могут быть одновременно истинными: истинность одного из них обязательно означает ложность другого. Например, суждения: «Все школьники изучают математику», «Некоторые школьники не изучают математику», – не могут быть одновременно истинными и являются несовместимыми (истинность первого суждения с неизбежностью приводит к ложности второго).

Совместимые суждения могут находиться в следующих отношениях:
1. Равнозначность – это отношение между двумя суждениями, у которых и субъекты, и предикаты, и связки, и кванторы совпадают. Например, суждения: «Москва является древним городом», «Столица России является древним городом», – находятся в отношении равнозначности.

2. Подчинение – это отношение между двумя суждениями, у которых предикаты и связки совпадают, а субъекты находятся в отношении вида и рода. Например, суждения: «Все растения являются живыми организмами», «Все цветы (некоторые растения) являются живыми организмами», – находятся в отношении подчинения.

3. Частичное совпадение (субконтрарность) – это отношение между двумя суждениями, у которых субъекты и предикаты совпадают, а связки различаются. Например, суждения: «Некоторые грибы являются съедобными», «Некоторые грибы не являются съедобными», – находятся в отношении частичного совпадения.
Необходимо отметить, что в этом отношении находятся только частные суждения – частноутвердительные (I) и частноотрицательные (O).

Несовместимые суждения могут находиться в следующих отношениях.
1. Противоположность (контрарность) – это отношение между двумя суждениями, у которых субъекты и предикаты совпадают, а связки различаются. Например, суждения: «Все люди являются правдивыми», «Все люди не являются правдивыми», – находятся в отношении противоположности.
В этом отношении могут быть только общие суждения – общеутвердительные (A) и общеотрицательные (E).

Важным признаком противоположных суждений является то, что они не могут быть одновременно истинными, но могут быть одновременно ложными.
Так, два приведённых противоположных суждения не могут быть одновременно истинными, но могут быть одновременно ложными: неправда, что все люди являются правдивыми, но также неправда, что все люди не являются правдивыми.

Противоположные суждения могут быть одновременно ложными, потому что между ними, обозначающими какие-то крайние варианты, всегда есть третий, средний, промежуточный вариант. Если этот средний вариант будет истинным, то два крайних окажутся ложными.
Между противоположными (крайними) суждениями: «Все люди являются правдивыми», «Все люди не являются правдивыми», – есть третий, средний вариант: «Некоторые люди являются правдивыми, а некоторые не являются таковыми», – который, будучи истинным суждением, обусловливает одновременную ложность двух крайних, противоположных суждений.

2. Противоречие (контрадикторность) – это отношение между двумя суждениями, у которых предикаты совпадают, связки различны, а субъекты отличаются своими объёмами, т. е. находятся в отношении подчинения (вида и рода).
Например, суждения: «Все люди являются правдивыми», «Некоторые люди не являются правдивыми», – находятся в отношении противоречия.

Важным признаком противоречащих суждений, в отличие от противоположных, является то, что между ними не может быть третьего, среднего, промежуточного варианта. В силу этого два противоречащих суждения не могут быть одновременно истинными и не могут быть одновременно ложными: истинность одного из них обязательно означает ложность другого, и наоборот – ложность одного обусловливает истинность другого.

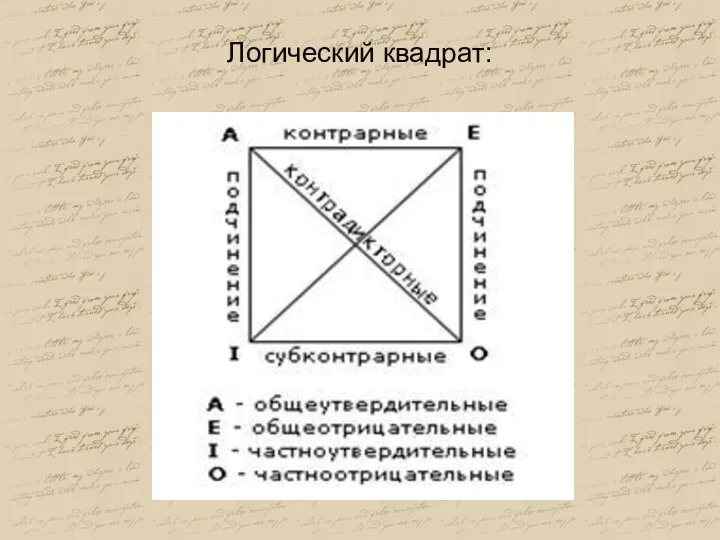
Рассмотренные отношения между простыми сравнимыми суждениями изображаются схематически с помощью логического квадрата который был разработан ещё средневековыми логиками.
Вершины квадрата обозначают четыре вида простых суждений, а его стороны и диагонали – отношения между ними.
Так, суждения вида A и вида I , а также суждения вида E и вида O находятся в отношении подчинения. Суждения вида A и вида E находятся в отношении противоположности, а суждения вида I и вида O – частичного совпадения. Суждения вида A и вида O , а также суждения вида E и вида I находятся в отношении противоречия.

Логический квадрат:

1. Если А истинно, то Е ложно, О ложно, I истинно.
2. Если Е истинно, то А ложно, I ложно, О истинно.
3. Если I ист, то А неопред, О неопред, Е ложно.
4. Если О ист, то Е непр, I неопр, А ложно.
5. Если А ложно, то Е неопр, I неопр, О истинно.
6. Если Е ложно, то А неопр, I истинно, О неопр.
7. Если I ложно, то А ложно, Е истинно, О истинно.
8. Если О ложно, то А истинно, Е ложно, I истинно.

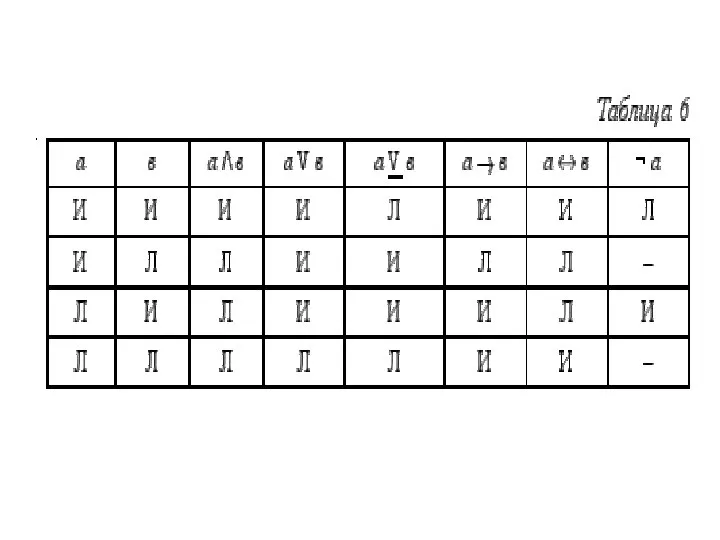
5.
В зависимости от союза, с помощью которого простые суждения соединяются в сложные, выделяется пять видов сложных суждений:
1. Конъюнктивное суждение (конъюнкция) – это сложное суждение с соединительным союзом «и», который обозначается в логике условным знаком «∧». С помощью этого знака конъюнктивное суждение, состоящее из двух простых суждений, можно представить в виде формулы: a ∧ b (читается «a и b »), где a и b – это два каких-либо простых суждения.

Например, сложное суждение: «Сверкнула молния, и загремел гром», – является конъюнкцией (соединением) двух простых суждений: «Сверкнула молния», «Загремел гром». Конъюнкция может состоять не только из двух, но и из большего числа простых суждений. Например: «Сверкнула молния, и загремел гром, и пошёл дождь (a ∧ b ∧ c )».

2. Дизъюнктивное суждение (дизъюнкция) – это сложное суждение с разделительным союзом «или». Союз или может использоваться как в нестрогом (неисключающем) значении, так и в строгом (исключающем).
Поэтому, что дизъюнктивные суждения делятся на два вида:

1. Нестрогая дизъюнкция – это сложное суждение с разделительным союзом «или» в его нестрогом (неисключающем) значении, который обозначается условным знаком «V».
С помощью этого знака нестрогое дизъюнктивное суждение, состоящее из двух простых суждений, можно представить в виде формулы: a V b
(читается «a или b »), где a и b – это два простых суждения.

Например, сложное суждение: «Он изучает английский, или он изучает немецкий », – является нестрогой дизъюнкцией (разделением) двух простых суждений: «Он изучает английский», «Он изучает немецкий».
Эти суждения друг друга не исключают, ведь возможно изучать и английский, и немецкий одновременно, поэтому данная дизъюнкция является нестрогой.

2. Строгая дизъюнкция – это сложное суждение с разделительным союзом «или» в его строгом (исключающем) значении, который обозначается условным знаком «V».
С помощью этого знака строгое дизъюнктивное суждение, состоящее из двух простых суждений, можно представить в виде формулы: a V b (читается «или a , или b »), где a и b – это два простых суждения.

Например, сложное суждение: «Он учится в 9 классе, или он учится в 11 классе», – является строгой дизъюнкцией (разделением) двух простых суждений: «Он учится в 9 классе», «Он учится в 11 классе».
Эти суждения друг друга исключают, ведь невозможно одновременно учиться и в 9, и в 11 классе (если он учится в 9 классе, то точно не учится в 11 классе, и наоборот), в силу чего данная дизъюнкция является строгой.

3. Импликативное суждение (импликация) – это сложное суждение с условным союзом «если … то», который обозначается условным знаком «→».
С помощью этого знака импликативное суждение, состоящее из двух простых суждений, можно представить в виде формулы: a → b (читается «если a, то b »), где a и b – это два простых суждения.

Например, сложное суждение:
«Если вещество является металлом, то оно электропроводно», – импликативное суждение (причинно-следственную связь) двух простых суждений: «Вещество является металлом», «Вещество электропроводно».
В данном случае эти два суждения связаны таким образом, что из первого вытекает второе (если вещество – металл, то оно обязательно электропроводно), однако из второго не вытекает первое (если вещество электропроводно, то это вовсе не означает, что оно является металлом).

Первая часть импликации называется основанием, а вторая – следствием;
из основания вытекает следствие, но из следствия не вытекает основание. Формулу импликации: a → b , можно прочитать так: «если a, то обязательно b, но если b, то не обязательно a».

4. Эквивалентное суждение (эквиваленция) – это сложное суждение с союзом «если … то» не в его условном значении (как в случае с импликацией), а в тождественном (эквивалентном). В данном случае этот союз обозначается условным знаком «↔», с помощью которого эквивалентное суждение, состоящее из двух простых суждений, можно представить в виде формулы: a ↔ b (читается «если a, то b, и если b, то a»), где a и b – это два простых суждения.

Например, сложное суждение: «Если число является чётным, то оно делится без остатка на 2», – представляет собой эквивалентное суждение (равенство, тождество) двух простых суждений:
«Число является чётным», «Число делится без остатка на 2». В данном случае два суждения связаны так, что из первого вытекает второе, а из второго – первое: если число чётное, то оно обязательно делится без остатка на 2, а если число делится без остатка на 2, то оно обязательно чётное.

5. Отрицательное суждение (отрицание) – это сложное суждение с союзом «неверно, что…», который обозначается условным знаком «¬». С помощью этого знака отрицательное суждение можно представить в виде формулы: ¬a (читается «неверно, что a»), где a – это простое суждение.
В записи: ¬a, уже присутствуют два простых суждения: a – это какое-то утверждение, а знак «¬» – его отрицание. Перед нами как бы два простых суждения – одно утвердительное, другое – отрицательное. Пример отрицательного суждения: «Неверно, что все мухи являются птицами».

Итак, мы рассмотрели пять видов сложных суждений: конъюнкцию, дизъюнкцию (нестрогую и строгую), импликацию, эквиваленцию и отрицание.
Любое сложное суждение является истинным или ложным в зависимости от истинности или ложности входящих в него простых суждений.