Содержание
- 2. Гидроаэромеханика — (раздел механики, изучающий равновесие и движение жидкостей и газов, их взаимодействие между собой и
- 3. Если в покоящуюся жидкость поместить тонкую пластинку, то части жидкости, находящиеся по разные стороны от нее,
- 4. Единица давления—Паскаль (Па): 1 Па равен давлению, создаваемому силой 1 Н, равномерно распределенной по нормальной к
- 5. Если жидкость несжимаема, то ее плотность не зависит от давления. Тогда при поперечном сечении S, высоте
- 6. § 29. Уравнение неразрывности Движение жидкости называется течением, а совокупность частиц движущейся жидкости — потоком. Графически
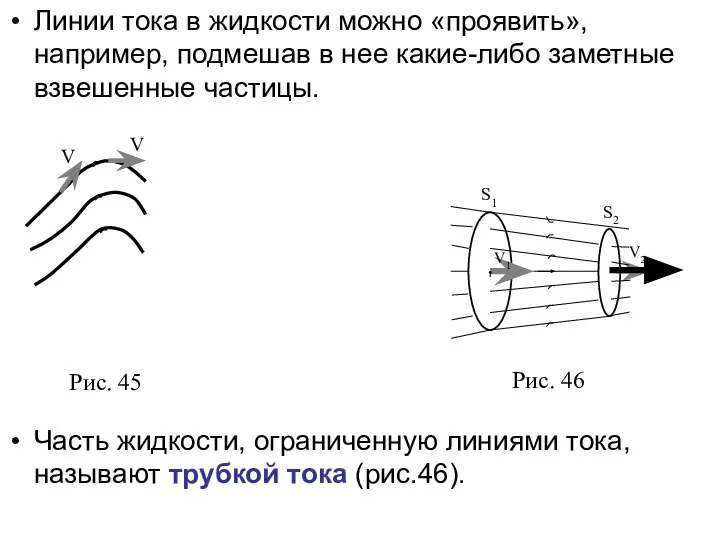
- 7. Линии тока в жидкости можно «проявить», например, подмешав в нее какие-либо заметные взвешенные частицы. Часть жидкости,
- 8. Течение жидкости называется установившимся (или стационарным), если форма и расположение линий тока, а также значения скоростей
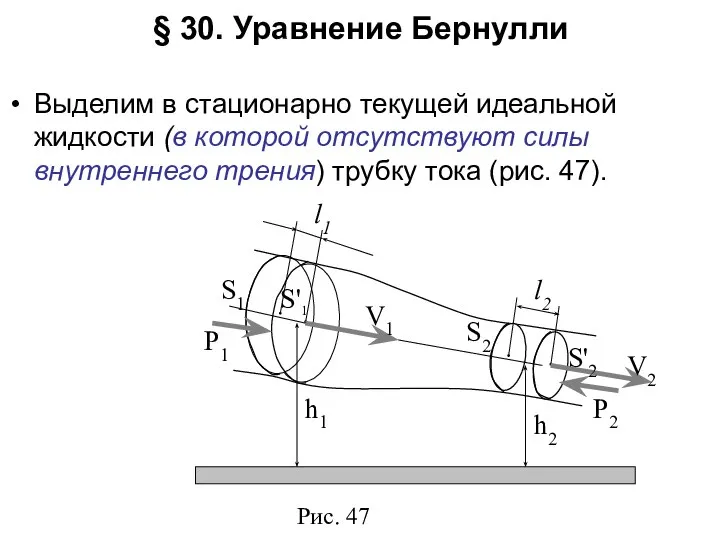
- 9. § 30. Уравнение Бернулли Выделим в стационарно текущей идеальной жидкости (в которой отсутствуют силы внутреннего трения)
- 10. Согласно закону сохранения энергии, изменение полной энергии идеальной несжимаемой жидкости должно быть равно работе А внешних
- 11. Для перенесения массы m от до жидкость должна переместиться на расстояние и от до — на
- 12. Полные энергии и будут складываться из кинетической и потенциальной энергий массы m жидкости: Подставляя (30.3) и
- 13. Согласно уравнению неразрывности для несжимаемой жидкости (29.1), объем, занимаемый жидкостью, остается постоянным, т. е. Разделив выражение
- 14. Так как сечения выбирались произвольно, то можем записать Выражение (30.6) называется уравнением Бернулли. Это уравнение —
- 15. Величина р в формуле (30.6) называется статическим давлением (давление жидкости на поверхность обтекаемого ею тела), величина
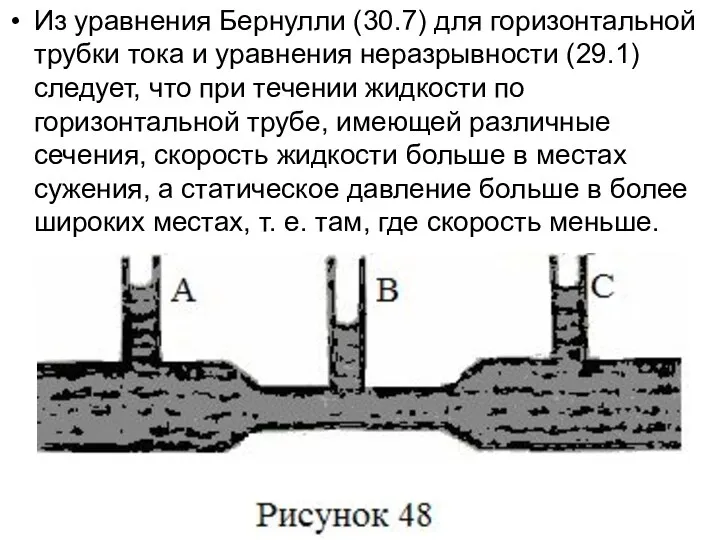
- 16. Из уравнения Бернулли (30.7) для горизонтальной трубки тока и уравнения неразрывности (29.1) следует, что при течении
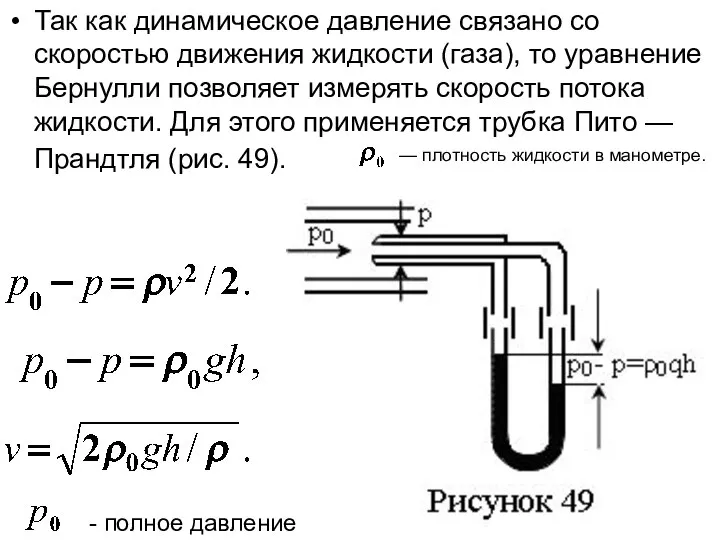
- 17. Так как динамическое давление связано со скоростью движения жидкости (газа), то уравнение Бернулли позволяет измерять скорость
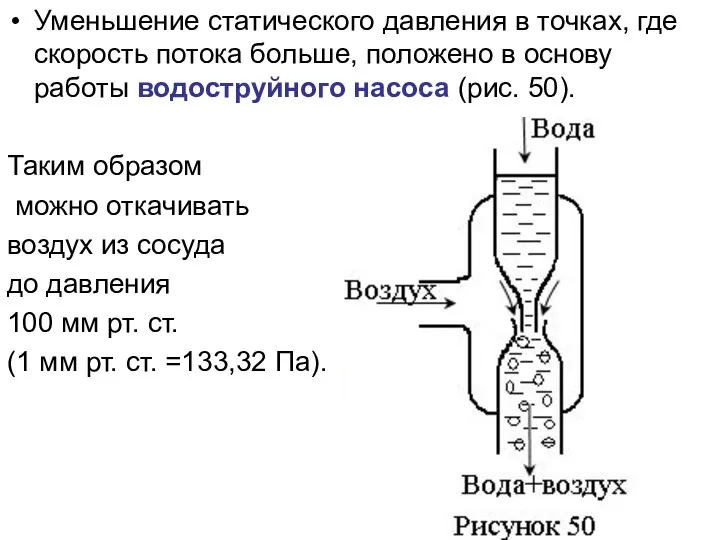
- 18. Уменьшение статического давления в точках, где скорость потока больше, положено в основу работы водоструйного насоса (рис.
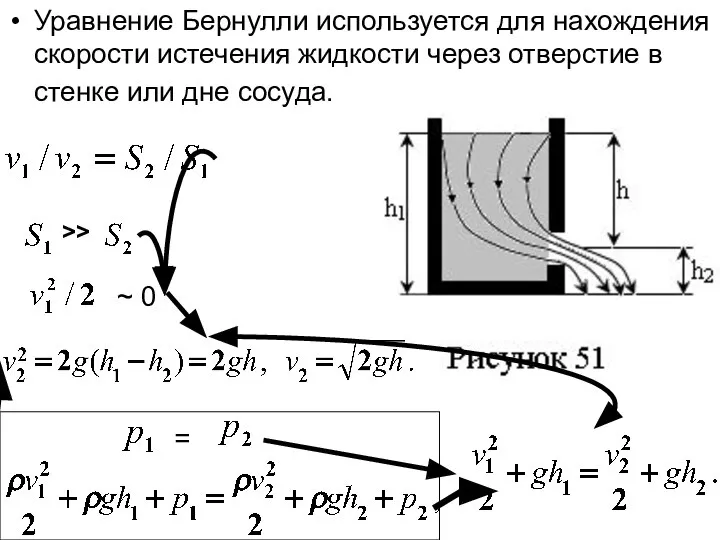
- 19. Уравнение Бернулли используется для нахождения скорости истечения жидкости через отверстие в стенке или дне сосуда. =
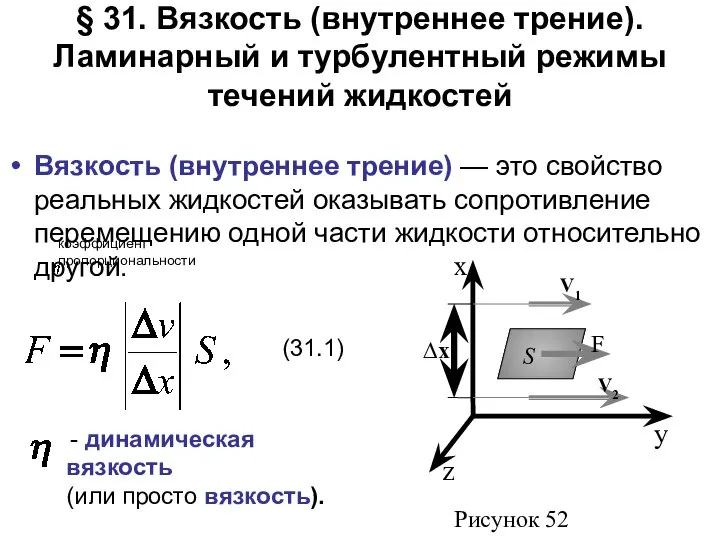
- 20. § 31. Вязкость (внутреннее трение). Ламинарный и турбулентный режимы течений жидкостей Вязкость (внутреннее трение) — это
- 21. Единица вязкости — паскаль-секунда (Па·с): 1 Па⋅с равен динамической вязкости среды, в которой при ламинарном течении
- 22. Существует два режима течения жидкостей. Течение называется ламинарным (слоистым), если вдоль потока каждый выделенный тонкий слой
- 23. где — кинематическая вязкость; — плотность жидкости; — средняя по сечению трубы скорость жидкости; d —
- 24. Профили скорости течения жидкости при ламинарном и турбулентном режимах
- 25. § 32. Методы определения вязкости 1. Метод Стокса. На шарик, падающий в жидкости вертикально вниз, действуют
- 26. При равномерном движении шарика или откуда Измерив скорость равномерного движения шарика, можно определить вязкость жидкости (газа).
- 27. 2. Метод Пуазейля Рассмотрим капилляр радиусом R и длиной . В жидкости мысленно выделим цилиндрический слой
- 28. Для установившегося течения жидкости сила внутреннего трения, действующая на боковую поверхность цилиндра, уравновешивается силой давления, действующей
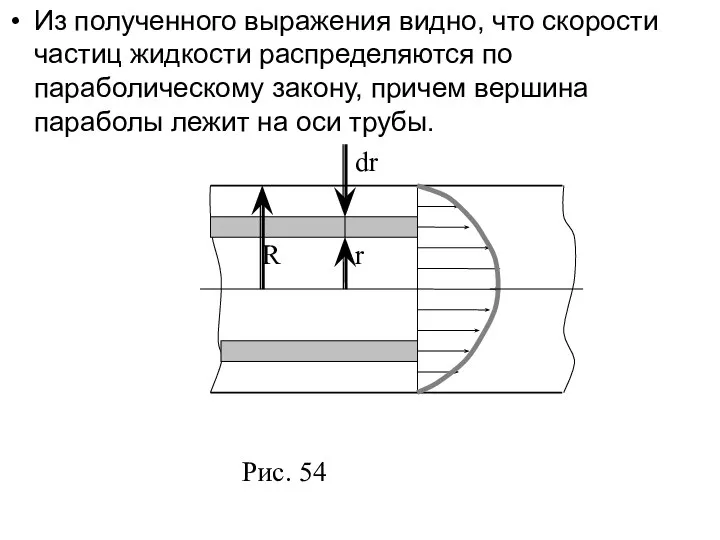
- 29. Из полученного выражения видно, что скорости частиц жидкости распределяются по параболическому закону, причем вершина параболы лежит
- 30. За время t из трубы вытечет жидкость, объем которой откуда вязкость
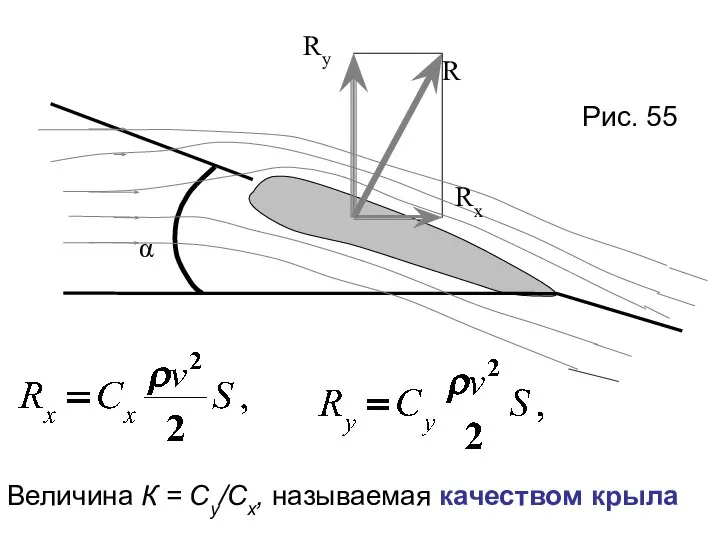
- 31. § 33. Движение тел в жидкостях и газах Одной из важнейших задач аэро- и гидродинамики является
- 32. Рис. 55 Величина К = Су/Сх, называемая качеством крыла
- 34. Скачать презентацию






















 Презентация на тему Последовательное соединение проводников (8 класс)
Презентация на тему Последовательное соединение проводников (8 класс)  Презентация на тему Гелиоцентрическая система Николая Коперника
Презентация на тему Гелиоцентрическая система Николая Коперника  Расчет сопротивления проводника. Удельное сопротивление. 24.02.2012г.
Расчет сопротивления проводника. Удельное сопротивление. 24.02.2012г. Указание по аварийной разблокировке с помощью торцевого ключа
Указание по аварийной разблокировке с помощью торцевого ключа Сила трения
Сила трения Полупроводники. Свойства полупроводников
Полупроводники. Свойства полупроводников Электрондық гармоникалық сигнал генераторлары Шаршы толқын генераторлары
Электрондық гармоникалық сигнал генераторлары Шаршы толқын генераторлары Основа классической динамики – три закона Ньютона (1686 год)
Основа классической динамики – три закона Ньютона (1686 год) Оптические приборы
Оптические приборы Измерение температуры с помощью термометра
Измерение температуры с помощью термометра Начала термодинамики
Начала термодинамики Молекулярно-кинетическая теория. Начала термодинамики
Молекулярно-кинетическая теория. Начала термодинамики Предмет изучения физики
Предмет изучения физики Равномерное движение по окружности
Равномерное движение по окружности Физика и познание мира
Физика и познание мира Ток в электролитах
Ток в электролитах Расчет стабилизированного источника питания
Расчет стабилизированного источника питания Турбина. Ротор
Турбина. Ротор Основные сведения о строении атома
Основные сведения о строении атома Презентация на тему История создания тепловых двигателей
Презентация на тему История создания тепловых двигателей 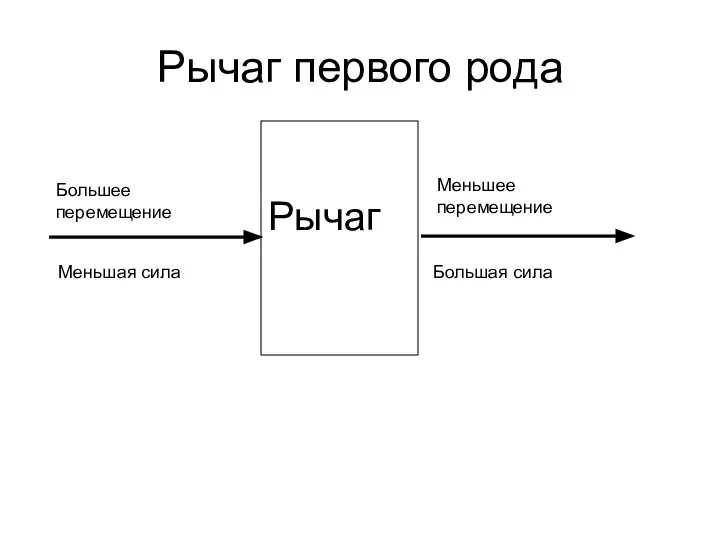 Рычаг первого рода
Рычаг первого рода Термоэлектрические преобразователи (термопара). Область применения
Термоэлектрические преобразователи (термопара). Область применения Презентация на тему Скорость прямолинейного равноускоренного движения
Презентация на тему Скорость прямолинейного равноускоренного движения  Электромагнитная индукция
Электромагнитная индукция Индукция
Индукция OVZ_Zanyatie_3
OVZ_Zanyatie_3 Механика. Кинематика - начальные понятия
Механика. Кинематика - начальные понятия Сверхпроводимость. Свойства
Сверхпроводимость. Свойства