Топология квантовой физики

Базовый концепт допущения тренога
Допущение:
Треног устойчивая конструкция. Пример: табуретка треног не шатается.
Из трёх абстрактов не имеющих чётких границ собственного определения формируется целостный конструктив
«Я» (наблюдатель) наблюдает «Ценность» и настолько насколько он плотно он видит ценность ценностью, настолько он получает структурирующий его как наблюдателя потенциал, и соответственно, Наблюдатель, качеством своего наблюдения идентифицирует энерго-потенциал, который получает Ценность в качестве структуроформируещего потенциала сохранения свойств Ценности.
Короче, насколько хорошо наблюдатель выполняет свою функцию наблюдать ценность, настолько сохранной является вся конструкция концепта тренога.

Векторная пространственность: Интеграл в «Треног шаг 2»
Пройдя по кругу, Абстракты обмениваются свойствами и формируют 3D матрицу векторальных корреляций.
Сопричастность всех новых элементов со всеми предыдущими элементами формируют 3D матрицу векторальных корреляций, т.е. модель векторного пространства.
Выборка свойств в массиве отражающая критическое значения Наблюдателя идентифицирует, в том числе, пространственную перспективу, так как любая сопричастность элементов и появления усложнённых элементов структуры учитывает шаги фрактализации сложности всей системы.
Короче: мы получили пространство для наблюдателя почти такое же, к которому привыкли: уже есть 3ёх-мерность и перспектива.
ЯЭнергия
ЦенностьЯ
ЭнергияЦенность
ЯЦенность
ЦенностьЭнергия
ЭнергияЯ
ЯЦенность
Я
ЦенностьЭнергия
Я
ЭнергияЯ
Я
И т.д.

Прекурсор векторной структуры наблюдателя “Das VektorGeschtalt”: Дифференциал «Тренога шаг 2»
Дифференциал Функционала Наблюдателя с точки зрения минимума сечений Векторной Пространственности Наблюдателя:
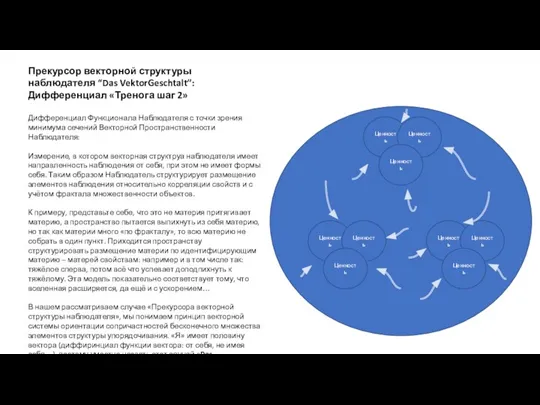
Измерение, в котором векторная структруа наблюдателя имеет направленность наблюдения от себя, при этом не имеет формы себя. Таким образом Наблюдатель структурирует размещение элементов наблюдения относительно корреляции свойств и с учётом фрактала множественности объектов.
К примеру, представьте себе, что это не материя притягивает материю, а пространство пытается выпихнуть из себя материю, но так как материи много «по фракталу», то всю материю не собрать в один пункт. Приходится пространству структурировать размещение материи по идентифицирующим материю – матерей свойствам: например и в том числе так: тяжёлое сперва, потом всё что успевает доподпихнуть к тяжёлому. Эта модель показательно соответствует тому, что вселенная расширяется, да ещё и с ускорением…
В нашем рассматриваем случае «Прекурсора векторной структуры наблюдателя», мы понимаем принцип векторной системы ориентации сопричастностей бесконечного множества элементов структуры упорядочивания. «Я» имеет половину вектора (диффиринциал функции вектора: от себя, не имея себя…), поэтому уместно назвать этот случай «Das VektorGeschtalt Наблюдателя».

Функционал очерёдности уплотнения пространственных мерностей
Функционала Наблюдателя с каждым шагом фрактализации своих свойств получает дополнительную пространственность в своей векторной схеме:
К примеру: мы имеем векторную пространственность «Треног шаг 2», т.е. у наблюдателя уже есть 3ёх-мерность и перспектива. Теперь к этой моделе применяется так же «Das VektorGeschtalt Наблюдателя». В результате мы получаем 3ёх мерность с правилами структуризации элементов.
При этом мы помним, что в свойствах уплотнения сопричатсностей элемнентов всегда учитываются уже сложившиеся сопричастности.
Поэтому «Das VektorGeschtalt Наблюдателя» является неотъемлемой частью фрактала свойств наблюдателя и представлен в таком порядке специально для упрощённого-последовательного ознакомления с общим макрамэ всей этой херни.