Prezentatsia_po_lektsii_6

Атом водорода и водородоподобные системы - это системы, состоящие из ядра с зарядом Ze и одного электрона (например, ионы He+ или Li++).
Решение задачи об энергетических уровнях электрона для атома водорода (а также водородоподобных систем: иона гелия He+ , двукратно ионизированного лития Li++ и др.) сводится к задаче о движении электрона в кулоновском поле ядра.
Потенциальная энергия взаимодействия электрона с ядром, обладающим зарядом Ze (для атома водорода Z = 1).

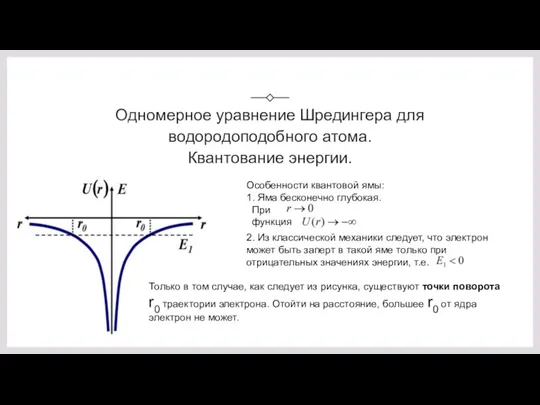
Одномерное уравнение Шредингера для водородоподобного атома.
Квантование энергии.
Особенности квантовой ямы:
1. Яма бесконечно глубокая.
При
функция
2. Из классической механики следует, что электрон может быть заперт в такой яме только при отрицательных значениях энергии, т.е.
Только в том случае, как следует из рисунка, существуют точки поворота r0 траектории электрона. Отойти на расстояние, большее r0 от ядра электрон не может.

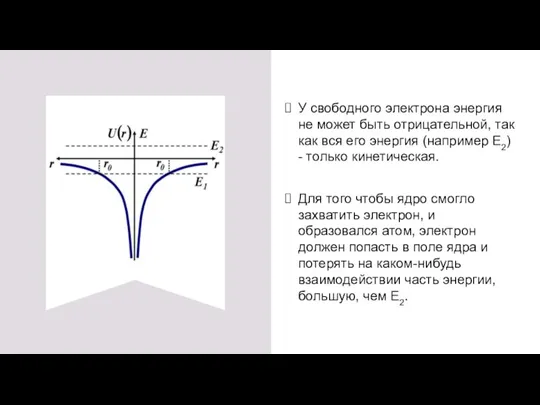
У свободного электрона энергия не может быть отрицательной, так как вся его энергия (например E2) - только кинетическая.
Для того чтобы ядро смогло захватить электрон, и образовался атом, электрон должен попасть в поле ядра и потерять на каком-нибудь взаимодействии часть энергии, большую, чем E2.

Квантово-механическая модель атома водорода
Решение уравнения Шредингера для электрона в центрально-симметричном поле ядра
Система: ядро с зарядом +Ze и один электрон:
Где E - полная энергия системы, а U - потенциальная энергия системы

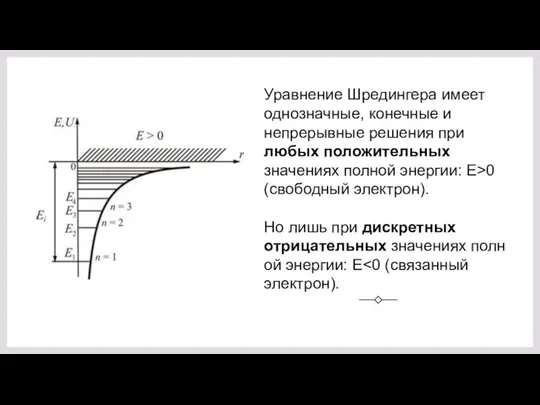
Уравнение Шредингера имеет однозначные, конечные и непрерывные решения при любых положительных значениях полной энергии: E>0 (свободный электрон).
Но лишь при дискретных отрицательных значениях полной энергии: E<0 (связанный электрон).

Результат решения: собственные значения энергии
Совпадает с En , полученной Бором. Но здесь получается из уравнения Шредингера, без каких либо дополнительных предположений.
n- главное квантовое число

Таким образом, как и в случае "потенциальной ямы" с бесконечно высокими "стенками", решение уравнения Шредингера для атома водорода приводит к появлению дискретных энергетических уровней. Самый нижний уровень E1, отвечающий минимальной возможной энергии, - основной, все остальные (En>E1, n=1,2,3,…) - возбужденные. При E<0 движение электрона является связанным, он находится внутри гиперболической "потенциальной ямы".
По мере роста главного квантового числа n энергетические уровни располагаются теснее и при
При E>0 движение электрона является свободным; область непрерывного спектра E>0
соответствует ионизированному атому.
Энергия ионизации атома водорода равна:

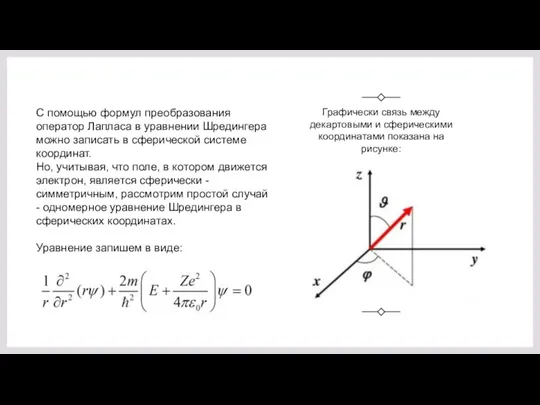
Так как "потенциальная яма" имеет центрально симметричную форму, то оператор Лапласа необходимо взять в сферической системе координат: .
Волновые функции в общем случае будут зависеть от координат .
Данная задача успешно решена в квантовой механике, но решение ее достаточно громоздкое, и мы его здесь не приводим. Рассмотрим лишь основные результаты, которые следуют из решения уравнения.
Собственные функции уравнения содержат три целочисленных параметра. Их называют квантовыми числами и обозначают n, l, m.
Параметр n называется главным квантовым числом. Оно определяет энергию электрона в атоме и может принимать любые целочисленные значения. Энергия электрона в атоме квантуется.

Графически связь между декартовыми и сферическими координатами показана на рисунке:
С помощью формул преобразования оператор Лапласа в уравнении Шредингера можно записать в сферической системе координат.
Но, учитывая, что поле, в котором движется электрон, является сферически - симметричным, рассмотрим простой случай - одномерное уравнение Шредингера в сферических координатах.
Уравнение запишем в виде:

Общее решение уравнения Шредингера, зависящее от всех трех сферических координат , может быть найдено методом разделения переменных.
В соответствии с этим методом волновая функция представляется в виде произведения двух сомножителей, один из которых зависит только от r, а другой - только от углов .
При этом оказывается, что имеющие физический смысл решения уравнения Шредингера при E<0 содержат уже не одно квантовое число n ,как это характерно для одномерных сферически-симметричных решений, а четыре квантовых числа .

Определим смысл квантовых чисел
Из квантовомеханических представлений: состояние электрона в атоме водорода полностью определяется значениями четырех физических величин:
Энергии E
Орбитального момента импульса L
Проекции Lz орбитального момента импульса на произвольно выбранное направление z
Проекции Lsz спинового момента импульса электрона на то же направление
Энергия. Возможные значения энергии электрона En в атоме (энергетические уровни) определяются главным квантовым числом n, принимающим целочисленные значения, начиная с единицы: n = 1, 2, 3,...

Орбитальный механический момент импульса L. Всякая частица, совершающая движение по траектории, обладает моментом импульса.
Это вектор, который по определению равен , где
- радиус-вектор частицы,
- ее импульс.
В квантовой механике вводятся четыре оператора, касающихся момента импульса: оператор квадрата момента, и три оператора проекций момента импульса на координатные оси.
Оказывается, что одновременно могут иметь определенные значения лишь квадрат момента и одна из проекций момента импульса. Это означает, что вектор момента импульса не имеет определенного направления и не может изображаться как в классической механике, отрезком прямой.

Из решения уравнения Шредингера вытекает, что механический орбитальный момент импульса электрона квантуется, т.е. не может быть произвольным, а принимает только определенные дискретные значения. Эти значения определяются формулой:
Где l - орбитальное квантовое число, которое при заданном n принимает значения
Таким образом, квантовое число l определяет момент импульса электрона в атоме.

Азимутальное (орбитальное) квантовое число
- азимутальное квантовое число
- определяет величину (модуль) момента импульса электрона в атоме:
Величина момента импульса квантована

Значения азимутального (орбитального) числа l при n > 1

Классификация стационарных состояний электрона в водородоподобном атоме
Энергетическому уровню может соответствовать несколько квантовых состояний.
В атомной физике используется система условных обозначений состояний электрона, заимствованная из спектроскопии.
Состояния с различными значениями азимутального квантового числа l различаются значениями момента импульса.
Электрон, находящийся в состоянии с l = 0, называется s - электроном, а его состояние - s - состоянием, с l = 1 называется p - электроном, с l = 2 - d - электроном.
Далее идут f, g, h - состояния и т.д. по алфавиту.
Значение главного квантового числа указывается перед условным обозначением квантового числа .
Пример: электрон в состоянии с n=3 и l = 1 обозначается символом 3p.

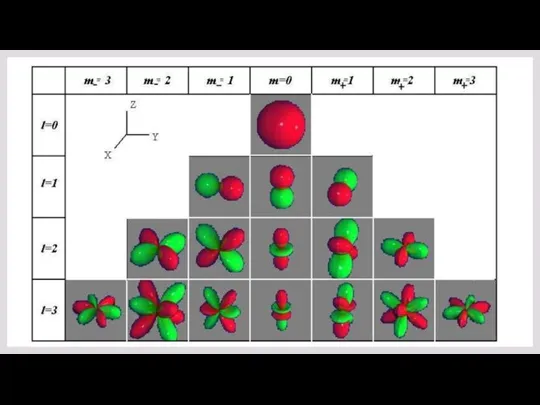
ОРБИТАЛЬНОЕ КВАНТОВОЕ
ЧИСЛО
ХАРАКТЕРИЗУЕТ ЭЛЛИПТИЧНОСТЬ ОРБИТЫ ЭЛЕКТРОНА И ОПРЕДЕЛЯЕТ МОМЕНТ ИМПУЛЬСА ЭЛЕКТРОНА
l=0
l=1
l=2
Состояния, соответствующие орбитальному числу l = 0, 1, 2, 3,…, также обозначаются буквами s, p, d, f,...
s – sharp, p – principal,
d – diffuse, f - fundamental

Различные состояния орбитального квантового числа электрона служат для систематики электронных состояний в атомах и молекулах. Приняты следующие обозначения:
l = 0, s - состояние
l = 1, p - состояние
l = 2, d - состояние
l = 3, f - состояние
Значение главного квантового числа указывается перед условным обозначением квантового числа l. Возможны следующие состояния электрона:
1s,
2s, 2p,
3s, 3p, 3d,
4s, 4p, 4d, 4f и т.д.

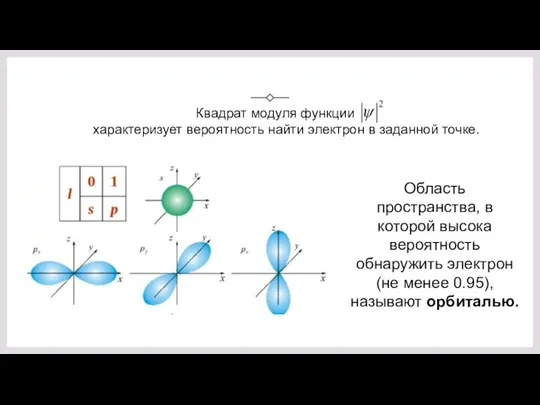
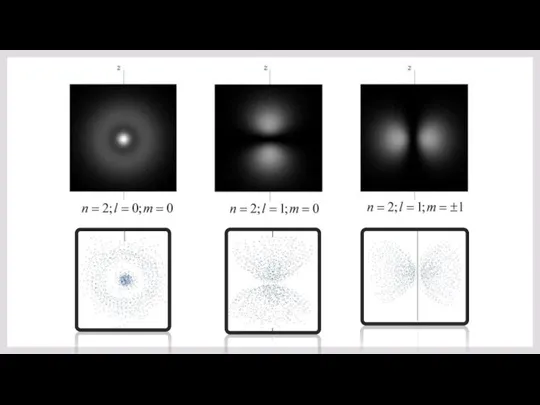
Квадрат модуля функции
характеризует вероятность найти электрон в заданной точке.
Область пространства, в которой высока вероятность обнаружить электрон (не менее 0.95), называют орбиталью.

Магнитное квантовое число
- магнитное квантовое число
определяет проекцию момента импульса на выделенное направление (например, направление магнит. или электр. поля).
Т.е. проекция момента импульса на некоторое выделенное направление принимает дискретные значения - пространственное квантование.
Например, электрон в атоме водорода в квантовом состоянии
Может иметь 5 значений для проекции момента импульса на заданное направление.

Атом водорода: вырожденные состояния
- главное квантовое число,
- азимутальное квантовое число,
- магнитное квантовое число,
Энергия зависит только от
Одному энергетическому состоянию может соответствовать несколько квантовых состояний электрона - вырожденные состояния. Число вырожденных состояний - кратность вырождения .

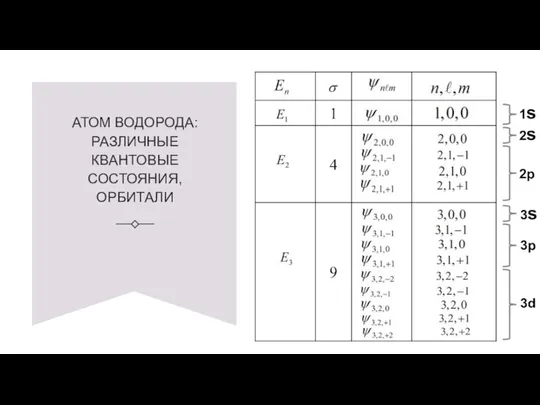
АТОМ ВОДОРОДА: РАЗЛИЧНЫЕ КВАНТОВЫЕ СОСТОЯНИЯ, ОРБИТАЛИ
1s
2s
3s
2p
3p
3d

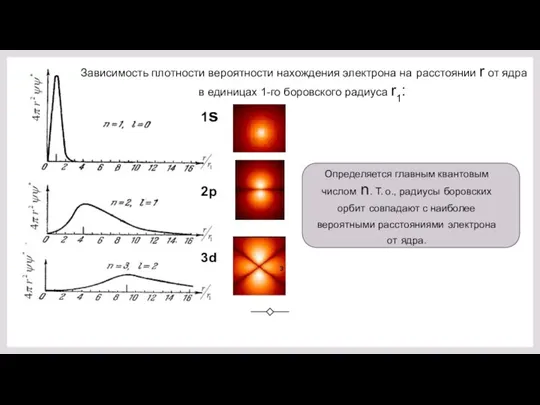
1s
2p
3d
Зависимость плотности вероятности нахождения электрона на расстоянии r от ядра в единицах 1-го боровского радиуса r1:
Определяется главным квантовым числом n. Т. о., радиусы боровских орбит совпадают с наиболее вероятными расстояниями электрона от ядра.

ОПЫТЫ ШТЕРНА И ГЕРЛАХА.
ПРОСТРАНСТВЕННОЕ КВАНТОВАНИЕ.
ОТКРЫТИЕ СПИНА ЭЛЕКТРОНА.
1922 Г.

Пучок атомов серебра пропускали через сильно неоднородное магнитное поле, создаваемое мощным постоянным магнитом. При прохождении атомов через это поле, в силу наличия у них магнитных моментов, на них действовала зависящая от проекции спина на направление магнитного поля сила, отклонявшая летящие между магнитами атомы от их первоначального направления движения. Если предположить, что магнитные моменты атомов ориентированы хаотично (непрерывно), то тогда на расположенной далее по направлению движения атомов пластинке должна была проявиться размытая полоса, но вместо этого на пластинке образовались две достаточно чёткие узкие полосы, что свидетельствовало в пользу того, что магнитные моменты атомов вдоль выделенного направления принимали лишь два определённых значения, что подтверждало предположение квантово-механической теории о квантовании магнитного момента атомов.

Вращающийся заряженный шарик должен обладать магнитным моментом, причем отношение магнитного момента к механическому должно иметь значение:
Первоначально предполагалось,
что спин обусловлен
вращением электрона вокруг
своей оси. Но пришлось
отказаться от подобных
модельных представлений, в частности по следующей
причине:

Электрон, наряду с собственным механическим моментом, обладает также и собственным магнитным моментом .
Но ряд опытных фактов, в частности аномальный эффект Зеемана, говорит о том, отношение собственных магнитного и механического моментов в 2 раза больше, чем для орбитальных моментов:
- собственный момент импульса электрона
Представление об электроне, как о вращающемся шарике оказалось несостоятельным.
Спин следует считать внутренним свойством, присущим электрону подобно тому, как ему присущи заряд и масса.

Наличие спина и все его свойства вытекают из установленного Дираком уравнения квантовой механики, удовлетворяющего требованиям теории относительности.
Поль Дирак

Спин электрона является свойством одновременно квантовым и релятивистским.
Спином обладают и другие элементарные частицы: протоны, нейтроны, фотоны и др.

Величина собственного момента импульса электрона определяется по общим законам квантовой механики так называемым спиновым квантовым числом s, равным :
Составляющая механического момента по заданному направлению может принимать квантовые значения:
где

Чтобы найти величину собственного магнитного момента электрона, умножим Ms на отношение
к Ms :
Знак минус указывает на то, что механический и магнитный моменты направлены в разные стороны.

Проекция собственного магнитного момента электрона на заданное направление может иметь следующие значения:
Минус получается, если
плюс - если

Проекция собственного момента импульса электрона может принимать значения
или
а собственного магнитного момента - значения
и
В ряд формул входят не сами моменты, а их проекции. Поэтому принято говорить, что собственный механический момент (спин) электрона равен половине (подразумевается в единицах ), а собственный магнитный момент равен одному магнетону Бора.

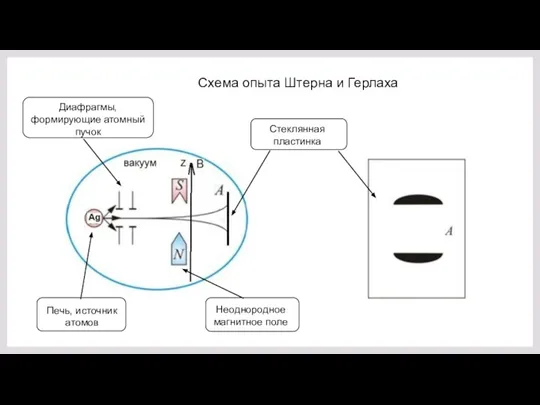
Схема опыта Штерна и Герлаха
Диафрагмы, формирующие атомный пучок
Печь, источник атомов
Неоднородное магнитное поле
Стеклянная пластинка

Идея опыта
Если магнитный момент атомов серебра равен
то в магнитном поле B, направленном по оси z, они приобретут добавочную энергию .
В классической теории
равно произведению магнитного момента на косинус угла между моментом и магнитным полем, так что дополнительная энергия в поле была бы равна:
Разумеется, когда атомы вылетают из печи, их магнитные моменты имеют любые направления, поэтому возможны все значения угла θ. Но если магнитное поле быстро изменяется с изменением z, т. е. если есть большой градиент, магнитная энергия с изменением положения тоже меняется, а поэтому на магнитные моменты действует сила, направление которой зависит от того, будет ли косинус положительным или отрицательным. Атомы при этом должны отклоняться вверх или вниз силой, пропорциональной производной магнитной энергии; из принципа виртуальной работы:

При отсутствии у атома магнитного момента (щелочные металлы, Ag) в опыте Штерна и Герлаха не должно наблюдаться расщепление атомного пучка.
Собственный магнитный момент электрона - спин
Опыт:
Расщепление есть на 2 полоски!!!
Гоудсмит и Уленбек (1925 г):
У электрона существует собственный магнитный момент импульса (спин) S и спиновый магнитный момент ps, который связан со спином соотношением:
в отличие от
Проекция спина на выделенное направление принимает всего два значения:
, где
- спиновое квантовое число

Принцип Паули. Распределению электронов по энергетическом уровням в атомах. Периодическая таблица элементов Менделеева.

Распределение электронов по энергетическим уровням в многоэлектронных атомах. Принцип Паули.
1) Квантовое состояние каждого электрона в атоме характеризуется 4-мя квантовыми числами:
Данному n соответствует n2 состояний, в которых могут находится не более 2n2 электронов (в слое).
2) Энергия квантового состояния в основном зависит от квантового числа n, слабее от l, еще слабее от m и еще слабее от .
3) В нормальном (невозбужденном) состоянии атома электроны располагаются на самых низких доступных для них энергетических уровнях.
4) Принцип Паули: в любой квантово-механической системе не может быть даже 2-ух электронов, обладающих одинаковой совокупностью 4-х квантовых чисел.

Электронная оболочка - совокупность электронов в атоме, состояния которых характеризуются определенными главным квантовым числом n и орбитальным числом l.
Согласно принципу Паули, максимальное значение числа электронов для данной электронной оболочки
Электронный слой - совокупность электронов с определенным n.
2 электрона
8 электронов
18 электронов
32 электрона
50 электронов
K - слой
L - слой​
M - слой
N - слой​
O - слой

Пример электронной конфигурации

Для полностью заполненной оболочки и, соответственно, слоя характерно равенство нулю суммарного орбитального и спинового моментов.
Состояния с различными значениями азимутального квантового числа l отличаются величиной момента импульса и формой распределения плотности вероятности:
Модуль момента импульса принимает дискретные значения:
Проекция момента импульса на некоторое выделенное направление определяется магнитным квантовым числом m:

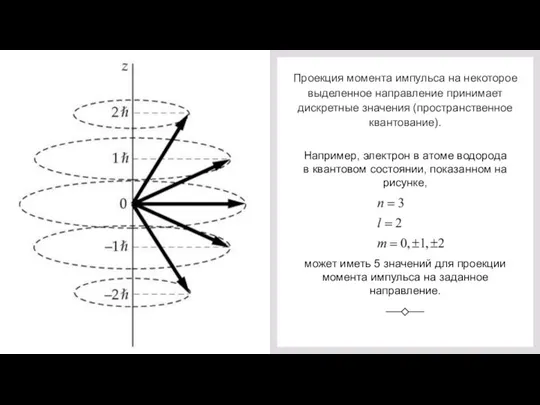
Проекция момента импульса на некоторое выделенное направление принимает дискретные значения (пространственное квантование).
Например, электрон в атоме водорода в квантовом состоянии, показанном на рисунке,
может иметь 5 значений для проекции момента импульса на заданное направление.

Правила отбора:
1s - основное состояние электрона в атоме водорода