Содержание
- 2. 1. В таблице дано число троллейбусных маршрутов в 10 крупных городах России. а) Найдите среднее арифметическое
- 3. 1. В таблице дано число троллейбусных маршрутов в 10 крупных городах России. а) Найдите среднее арифметическое
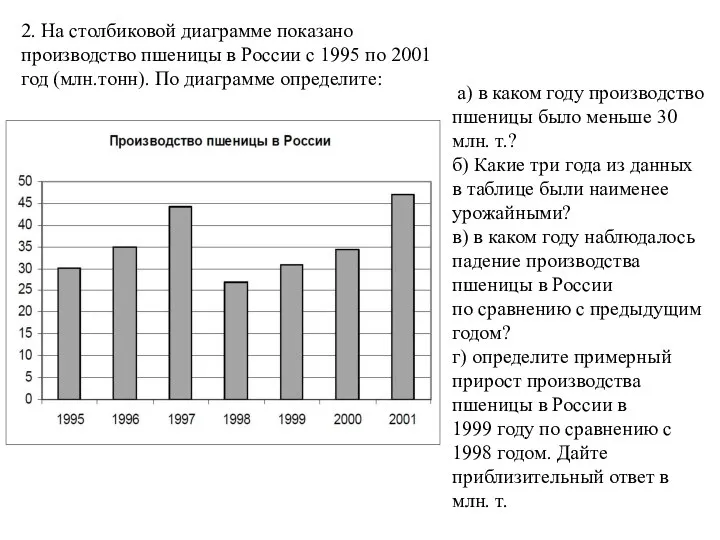
- 4. 2. На столбиковой диаграмме показано производство пшеницы в России с 1995 по 2001 год (млн.тонн). По
- 5. 2. На столбиковой диаграмме показано производство пшеницы в России с 1995 по 2001 год (млн.тонн). По
- 6. 3. Перед школьным спектаклем Саша, Вова и Коля с помощью жребия распределяют между собой роли Атоса,
- 7. 3. Перед школьным спектаклем Саша, Вова и Коля с помощью жребия распределяют между собой роли Атоса,
- 8. 4. Для проведения экзамена по математике в 9 классе случайным образом выбирается одна из 92 экзаменационных
- 9. 4. Для проведения экзамена по математике в 9 классе случайным образом выбирается одна из 92 экзаменационных
- 10. 5. На поле для игры в крестики-нолики поставлен крестик (см. рис.). Свободную клетку для нолика выбирают
- 11. 5. На поле для игры в крестики-нолики поставлен крестик (см. рис.). Свободную клетку для нолика выбирают
- 12. 6. В сундуке 5 монет, из которых 2 золотых и 3 серебряных. Пират достает из сундука
- 13. 6. В сундуке 5 монет, из которых 2 золотых и 3 серебряных. Пират достает из сундука
- 14. 2013Вар.1 Вариант 1
- 15. 2013Вар.1 Ответ: а) 2, 3, 4; б) число, близкое к 1000, например из интервала 900−1100. Примечание.
- 16. 2013Вар.1 Вариант 1
- 17. 2013Вар.1 Вариант 1 Ответ: а) 7; б) 4. Возможный ход решения. а) Среднее арифметическое: б) Отклонения
- 18. 2013Вар.1 Вариант 1
- 19. 2013Вар.1 Вариант 1 Ответ: а) 20; б) 10. Возможный ход решения: а) Каждый из 5 человек
- 20. 2013Вар.1 Вариант 1
- 21. 2013Вар.1 Вариант 1
- 22. 2013Вар.1 Вариант 1
- 23. 2013Вар.1 Вариант 1 Ответ: 0,3. Возможный ход решения. а) В среднем из 100 шорьков малиновых будет
- 24. 2013Вар.1 Вариант 1
- 25. 2013Вар.1 Вариант 1 Возможный ход решения. а) Вероятность того, что каждый отдельный автомат исправен, равна 1-
- 26. 2013Вар.1 Вариант 2
- 27. 2013Вар.1 Вариант 2 Ответ: а) 1, 3, 5; б) число, близкое к 3300, например, из интервала
- 28. 2013Вар.1 Вариант 2
- 29. 2013Вар.1 Вариант 2 Ответ: а) 8; б) 4.
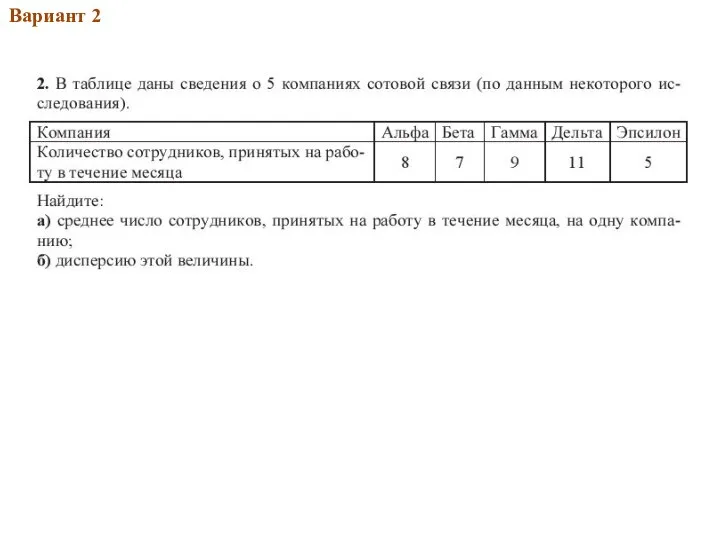
- 30. 2013Вар.1 Вариант 2
- 31. 2013Вар.1 Вариант 2 Ответ: а) 30; б) 15
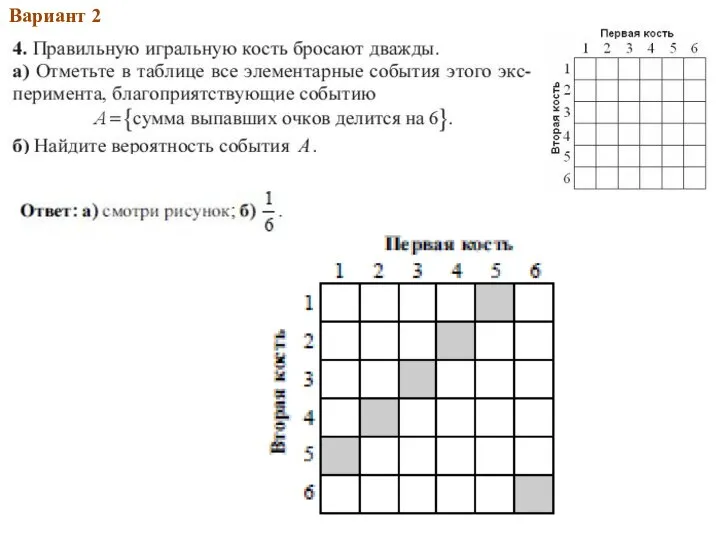
- 32. 2013Вар.1 Вариант 2
- 33. 2013Вар.1 Вариант 2
- 34. 2013Вар.1 Вариант 2
- 35. 2013Вар.1 Вариант 2 Ответ: 0,1.
- 36. 2013Вар.1 Вариант 2
- 37. 2013Вар.1 Вариант 2 Ответ: а) 0,027 .
- 39. Скачать презентацию

































 Линейная алгебра
Линейная алгебра Вычитание предшествующего числа
Вычитание предшествующего числа Векторы в пространстве
Векторы в пространстве Презентация по математике "Флеш - анимация на уроках математики в начальной школе" -
Презентация по математике "Флеш - анимация на уроках математики в начальной школе" -  Презентация по теории вероятностей. На тему:”Описательная статистика”.
Презентация по теории вероятностей. На тему:”Описательная статистика”. Теория игр
Теория игр Общее понятие меры
Общее понятие меры Четырехугольники
Четырехугольники Тренажер Умножение целых чисел
Тренажер Умножение целых чисел Построение фронтальной диметрической и изометрической проекций
Построение фронтальной диметрической и изометрической проекций Сложение и вычитание многочленов
Сложение и вычитание многочленов Система управління технологічного процесу приготування розчинів для піроксилінових порохів
Система управління технологічного процесу приготування розчинів для піроксилінових порохів Множення десяткових дробів
Множення десяткових дробів Периметр и площадь прямоугольника
Периметр и площадь прямоугольника Перпендикуляр и наклонная. Угол между прямой и плоскостью. 10 класс
Перпендикуляр и наклонная. Угол между прямой и плоскостью. 10 класс Твёрдые и мягкие согласные звуки. Сложение и вычитание без перехода через десяток
Твёрдые и мягкие согласные звуки. Сложение и вычитание без перехода через десяток Презентация на тему Вычитание трёхзначных чисел с переходом через разряд
Презентация на тему Вычитание трёхзначных чисел с переходом через разряд  Числовые неравенства и их свойства. Подготовка к ОГЭ
Числовые неравенства и их свойства. Подготовка к ОГЭ Презентация на тему Умножение и деление на 10 и 100
Презентация на тему Умножение и деление на 10 и 100  Подготовка к ЕГЭ
Подготовка к ЕГЭ Случаи сложения вида +7
Случаи сложения вида +7 Сказочная математика
Сказочная математика Математическая игра Гусеница
Математическая игра Гусеница Применение признаков подобия треугольников к решению задач и доказательству теорем
Применение признаков подобия треугольников к решению задач и доказательству теорем Математический анализ. Лекция 1
Математический анализ. Лекция 1 Презентация на тему КООРДИНАТНАЯ ПЛОСКОСТЬ (6 КЛАСС)
Презентация на тему КООРДИНАТНАЯ ПЛОСКОСТЬ (6 КЛАСС)  Симметрия. Осевая симметрия
Симметрия. Осевая симметрия Типовые дискретные последовательности
Типовые дискретные последовательности