Слайд 2Прямые измерения – это измерения, при которых искомое значение физической величины находят

непосредственно с помощью специальных технических средств. Например, измерение длины с помощью линейки, измерение массы с помощью весов и др.
Косвенные измерения – это измерения, при которых искомое значение физической величины находят с использованием формул
Однократное измерение – измерение, выполненное один раз. К данному виду измерений можно отнести: измерение массы детали, определение тока или напряжения на участках электрической цепи, измерение промежутка времени и т. п.
Слайд 3Погрешностью измерения называется отклонение измеренного значения от истинного значения измеряемой величины.
Абсолютная

погрешность измерения – это разница между измеренным и истинным значениями измеряемой величины, выраженная в единицах измеряемой величины.
В тех случаях, когда погрешность прибора не указана на шкале и не приведена в паспорте прибора, ее считают равной величине, соответствующей половине наименьшего деления шкалы.
Слайд 4ПРАВИЛА ПРЕДСТАВЛЕНИЯ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
Всякое число состоит из цифр, определяющих количество единиц в

различных разрядах числа. Например, в числе 1726,34 имеется шесть цифр.
Значащими цифрами числа являются все цифры данного числа, кроме нулей, стоящих слева. Нули, стоящие в середине или в конце числа (справа) являются значащими цифрами, так как обозначают отсутствие единиц в соответствующем разряде. При этом цифры множителя 10^n не учитываются.
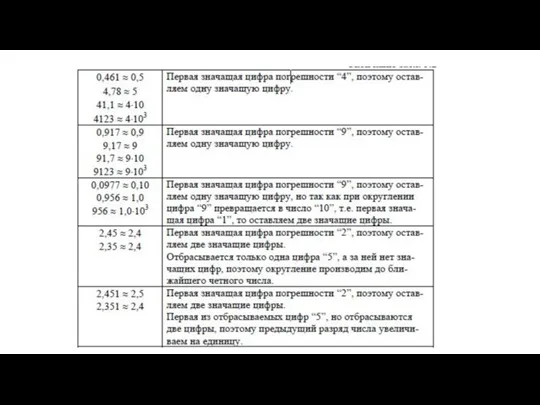
Слайд 6Погрешности измерения должны содержать не более двух (т. е. одну или две)

значащих цифры. Для этого следует использовать следующие правила и порядок ограничения числа значащих цифр.
Если первая значащая цифра в абсолютной погрешности Δx “1”, “2”, “3”, то в погрешности оставляем две значащие цифры.
Если первая значащая цифра в погрешности “4”, “5”, “6”, “7”, “8”, “9”, то в погрешности оставляем одну значащую цифру.
Измеренное значение x должно заканчиваться тем же младшим разрядом, что и абсолютная погрешность Δx . Например, если в абсолютной погрешности Δx оставлен младший разряд – единицы, то и в измеренном значении должен быть оставлен младший разряд – единицы.
Слайд 7При ограничении числа значащих цифр используем операцию округления. Округление числа представляет собой

отбрасывание значащих цифр справа после определенного разряда с возможным изменением цифры этого разряда.
Существуют следующие правила округления.
1. Если первая из отбрасываемых цифр меньше чем “5”, то цифра предыдущего разряда не изменяется.
2. Если первая из отбрасываемых цифр больше чем “5”или равна “5”, то цифра предыдущего разряда увеличивается на единицу.
3. Если отбрасывается только одна цифра “5”, а за ней нет цифр, то округление производится до ближайшего четного числа, т. е. цифра предыдущего разряда остается неизменной, если она четная, и увеличивается на единицу, если она нечетная.
5. Округление следует выполнять сразу до желаемого числа значащих цифр, а не по этапам, что может привести к ошибкам.











 Тепловые балансы ВТУ, их разновидности. Тепловой баланс теплотехнологического реактора
Тепловые балансы ВТУ, их разновидности. Тепловой баланс теплотехнологического реактора Закон сохранения и превращения энергии
Закон сохранения и превращения энергии Строение атома
Строение атома Презентация на тему Колебательное движение. Свободные колебания. Маятники (9 класс)
Презентация на тему Колебательное движение. Свободные колебания. Маятники (9 класс)  Сверхпроводимость материалов
Сверхпроводимость материалов Суд над атомом. Мультимедийный урок
Суд над атомом. Мультимедийный урок Динамика вращения. Закон динамики вращения
Динамика вращения. Закон динамики вращения Презентация на тему Сила упругости. Закон Гука. Вес тела
Презентация на тему Сила упругости. Закон Гука. Вес тела  Энергия магнитного поля
Энергия магнитного поля Оптические явления во сне и наяву
Оптические явления во сне и наяву Тест
Тест Автобус, двигаясь прямолинейно и равноускоренно
Автобус, двигаясь прямолинейно и равноускоренно Механические колебания
Механические колебания Измерение силы Архимеда
Измерение силы Архимеда СКОРОСТЬ СВЕТА
СКОРОСТЬ СВЕТА Порядок решения задач по динамике МТ
Порядок решения задач по динамике МТ Измерение линейных размеров штангенинструментом
Измерение линейных размеров штангенинструментом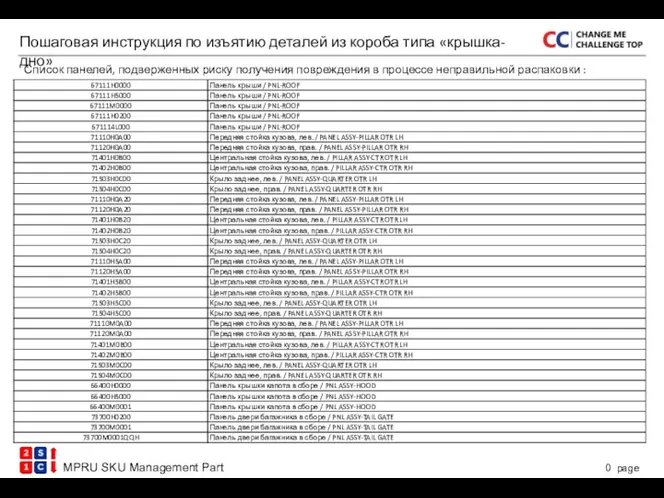 Пошаговая инструкция по изъятию деталей из короба типа крышка-дно
Пошаговая инструкция по изъятию деталей из короба типа крышка-дно Гидравлика и ГП
Гидравлика и ГП Исследование полей Токов смещения
Исследование полей Токов смещения Составные части машин
Составные части машин Презентация ЛЕКЦИЯ №11.0 колебания
Презентация ЛЕКЦИЯ №11.0 колебания Система. Объекты
Система. Объекты Частотные методы синтеза
Частотные методы синтеза з-н сохр.имп
з-н сохр.имп Презентация на тему Мощность
Презентация на тему Мощность  Презентация на тему Плазма (10 класс)
Презентация на тему Плазма (10 класс)  Летающие модели
Летающие модели