Специальная теория относительности

СТО
Теория относительности – физическая теория, рассматривающая пространственно-временные закономерности, справедливые для любых физических процессов (не только механических).
Из преобразований Галилея следовало, что все законы механики одинаковы во всех инерциальных системах отсчета (принцип относительности Галилея).

СТО
Однако законы электродинамики находились в противоречии с преобразованиями Галилея.
Эйнштейн заменил преобразования Галилея преобразованиями Лоренца, что устранило кажущееся противоречие и позволило объяснить многие опыты по электродинамике и оптике.

Постулаты Эйнштейна
В основу специальной теории относительности легли постулаты Эйнштейна:
1. Все физические явления протекают одинаково во всех инерциальных системах отсчета (принцип относительности Эйнштейна).
2. Скорость света в вакууме одинакова во всех инерциальных системах отсчета.

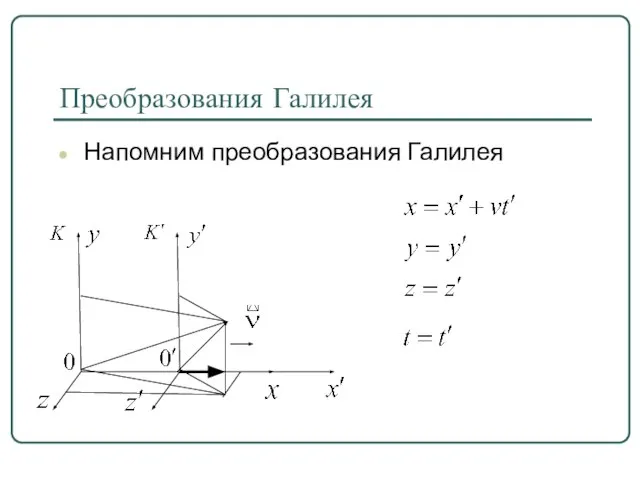
Преобразования Галилея
Напомним преобразования Галилея

Преобразования Лоренца
Получим преобразования Лоренца, опираясь на
постулаты Эйнштейна.
Учитывая однородность пространства и времени,
можно предположим, что новые преобразования
линейны, тогда
По принципу относительности все инерциальные
системы отсчета равноправны, следовательно,
можно записать

Преобразования Лоренца
Пусть в момент , когда начала систем отсчета К и K’ совпадали, произошла вспышка света. Тогда распространение света будет происходить по законам:
Следовательно,

Преобразования Лоренца
Подставив значение из второго уравнения в первое, получим
,
откуда

Преобразования Лоренца
Подставив значение в одну из формул
или
и решив полученное уравнение относительно t,
получим

Преобразования Лоренца
Преобразования Лоренца приобретают вид

Принцип соответствия
Преобразования Лоренца переходят в преобразования Галилея при условии
Таким образом, механика Ньютона является предельным случаем специальной теории относительности (принцип соответствия - новая теория, раскрывающая более глубоко физическую реальность, чем старая, включает последнюю как предельный (частный) случай).

Следствия из преобразований Лоренца. Относительность одновременности.
Относительность одновременности: события, одновременные в одной системе отсчета не одновременны в другой.
Когда ,

Следствия из преобразований Лоренца. Лоренцево сокращение длины.
Рассмотрим стержень, расположенный вдоль оси ,который покоится в системе .
Длина стержня в системе называется собственной длиной.
Длина движущегося стержня меньше собственной длины

Следствия из преобразований Лоренца. Длительность процессов.
Пусть в точке системы протекает процесс, длящийся
Найдем его длительность в системе

Следствия из преобразований Лоренца. Длительность процессов.
В - системе длительность процесса больше, в этой системе он протекает медленнее
Время , отсчитанное по часам, движущимся вместе с телом, называется собственным временем. Оно всегда меньше времени, отсчитанного по часам, движущимся относительно тела.

Интервал
Специальная теория относительности устанавливает связь пространства и времени, причем если время и пространство относительны, то величина
,
названная интервалом, абсолютна, т.е. инвариантна

Интервал
Интервал-это расстояние между двумя мировыми точками в едином четырехмерном пространстве. Бесконечно малый интервал является инвариантом
Четырехмерное пространство является псевдоэвклидовым, так как координатная и временная части входят в интервал с разными знаками.

Релятивистский закон сложения скоростей
Классический закон сложения скоростей неприменим при изучении электромагнитных явлений. Если воспользоваться преобразованиями Лоренца, то можно получить релятивистский закон сложения скоростей:

Релятивистский закон сложения скоростей
Проекции скорости тела в системах К и К' соответственно равны:

Релятивистский закон сложения скоростей
Дифференцируя преобразования Лоренца, найдем:

Релятивистский закон сложения скоростей
Разделим первые три равенства на последнее и учтем, что
получим

Релятивистский закон сложения скоростей

Энергия и импульс
Релятивистская энергия и релятивистский импульс будут определяться следующими выражениями:

Уравнение динамики
Основное уравнение динамики

Закон взаимосвязи массы и энергии
Закон взаимосвязи массы и энергии был установлен Эйнштейном и является фундаментальным законом природы
-энергия покоя
-энергия движения

Кинетическая энергия
Кинетическая энергия релятивистской частицы определяется

Связь между релятивистским импульсом и энергией
Запишем выражения для импульса и энергии и исключим из них скорость

Связь между релятивистским импульсом и энергией
После преобразований получим
Можно записать еще одну формулу

Безмассовые частицы
Рассмотрим частицу, движущуюся со скоростью света .
Для такой частицы . В соответствии с формулой
,
следовательно