Замедляющие структуры

Основные расчетные формулы:
1. Коэффициент замедления:
, (7.1)
где vф – фазовая скорость замедленной волны; – длина замедленной волны.
2. Коэффициент замедления спиральной структуры; (7.2)
где а и L – соответственно радиус и шаг спирали спиральной замедляющей структуры.
3. Коэффициент замедления гребенчатой структуры
, (7.3)

где d – глубина канавок замедляющей гребенчатой структуры.
4. Структура поля вдоль гребенчатой замедляющей структуры
(7.4)
(7.5)
где Em и Hm – амплитуды электрического и магнитного полей; – поперечное волновое число в воздухе, характеризующее затухание волны по мере удаления от поверхности замедляющей структуры;
– продольное волновое число, характеризующее изменение фазы волны при ее распространении вдоль замедляющей структуры; z и y – координаты, характеризующие изменение поля, соответственно, вдоль и поперек (от поверхности) замедляющей структуры.

5. Условие однородности замедляющей структуры
, (7.6)
где L – период замедляющей структуры (для спиральной структуры – шаг спирали).

Примеры решения типовых задач:
1. Показать, почему замедляющая структура может применяться в качестве волновода поверхностных волн?
Решение
Если основная часть электромагнитной энергии концентрируется в непосредственной близости от поверхности замедляющей структуры, она может быть применена в качестве волновода поверхностных волн. Оказывается, что даже при небольшом отличии vзот 1, явление это ярко выражено. Покажем это.
Пусть электромагнитное поле движется вдоль оси z (рисунок 7.1)

Рисунок 7.1
Среднее значение вектора Пойнтинга за период равно
.
На основании соотношений (7.4) и (7.5) справедливо, что

Определим мощность волн в сечении при x, равном единице длины:
.
При получим
Таким образом, в конечном, прилегающем к поверхности замедляющей структуры слое концентрируется часть энергии
.
Или с учетом, что ,
Определим теперь v3 в предположении, что 90% мощности находится в слое

.
Следовательно, .
Таким образом, при отличии коэффициента замедления всего на 0,09 от единицы основная часть (90%) электромагнитной энергии движется близко над замедляющей системой, что позволяет применить замедляющую систему в качестве линии передачи. Такие линии передачи (однопроводные) широко применяют в радиорелейных станциях связи.

2. Над замедляющей структурой возбуждается поверхностная волна с коэффициентом замедления vз=4. На каком расстоянии от замедляющей структуры напряженность поля уменьшится в e раз? Длина волны генератора см.
Решение
Согласно (7.4) известно, что продольная составляющая электрического поля убывает экспоненциально при удалении от поверхности y=0
.
Отношение амплитуд на поверхности замедляющей структуры и на расстоянии " y" по условию задачи равно е, тогда
.

Следовательно,
, или окончательно . Тогда можем записать
, ,
м.

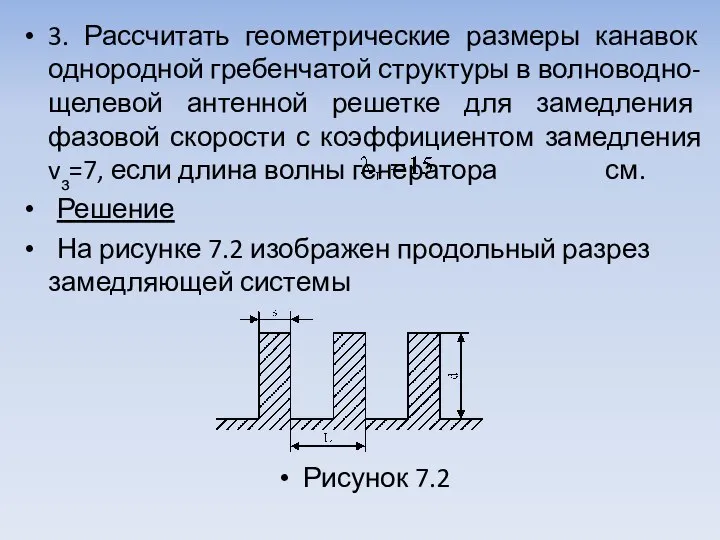
3. Рассчитать геометрические размеры канавок однородной гребенчатой структуры в волноводно-щелевой антенной решетке для замедления фазовой скорости с коэффициентом замедления vз=7, если длина волны генератора см.
Решение
На рисунке 7.2 изображен продольный разрез замедляющей системы
Рисунок 7.2

Глубину канавок найдем из выражения (7.3)
.
Так как система однородная, то на основании (7.6) будет справедливо
.
Выбираем L=2 мм.
Толщина зуба структуры s выбирается очень малой и обычно может быть определена из условий механической прочности и хорошего теплорассеяния.

4. Рассчитать геометрические размеры спирали лампы бегущей волны усилителя высокой частоты, в которой длина замедленной волны равна 0,08 м, а диаметр –1,5 см. Длина волны генератора м.
Решение
Шаг спирали определим из выражения (7.2)
.
На основании соотношения (7.1) справедливо, что
см.