Содержание
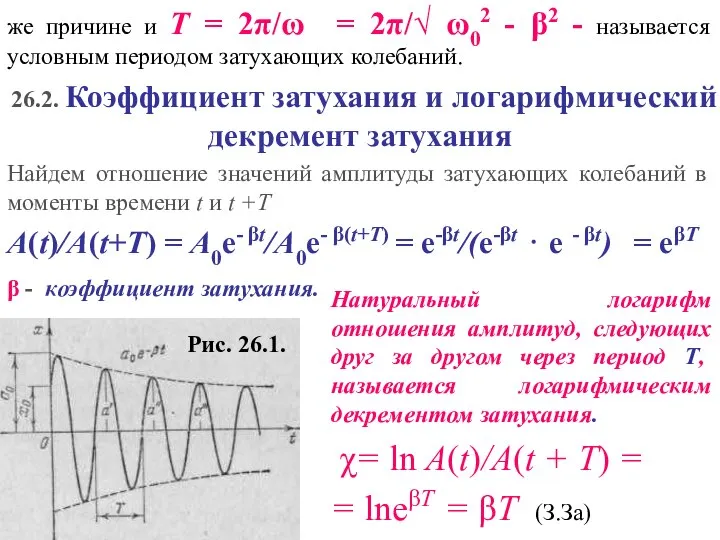
- 5. Рис. 26.1.
- 6. Выясним физический смысл χ и β Обозначим через τ -время, в течение которого амплитуда А уменьшается
- 8. Где ψ = arctg(β/ω). График этой функции изображен на рис. 26.2. Рис. 26.2.
- 10. перестает быть периодическим. При β > ω0 корни характеристичес- кого уравнения становятся вещественными и решение дифферен-
- 11. Это условие будет выполнено в том случае, если выведенной из положения равновесия системе сообщить достаточно сильный
- 14. Рис. 26.27.
- 17. Скачать презентацию
Слайд 5Рис. 26.1.
Рис. 26.1.
Слайд 6Выясним физический смысл χ и β
Обозначим через τ -время, в течение которого
Выясним физический смысл χ и β
Обозначим через τ -время, в течение которого

амплитуда А
уменьшается в e раз.
A0 /AΊ = eβτ = e1, откуда βτ = 1, β = 1/τ
Следовательно, коэффициент затухания β - есть физическая
величина, обратная времени, в течении которого амплитуда
уменьшается в е раз. τ - время релаксации.
Пусть Nе число колебаний, после которых амплитуда
уменьшается в e раз, τ - время этих колебаний,
тогда τ = ΝΤ, Τ= τ /Ν и χ = βΤ = τ / τ N = 1/N, χ = 1/N
Следовательно, логарифмический декремент затухания χ есть
физическая величина, обратная числу колебаний, по истечению
которых амплитуда А уменьшается в e раз. Если χ = 0,01,
то N = 100.
уменьшается в e раз.
A0 /AΊ = eβτ = e1, откуда βτ = 1, β = 1/τ
Следовательно, коэффициент затухания β - есть физическая
величина, обратная времени, в течении которого амплитуда
уменьшается в е раз. τ - время релаксации.
Пусть Nе число колебаний, после которых амплитуда
уменьшается в e раз, τ - время этих колебаний,
тогда τ = ΝΤ, Τ= τ /Ν и χ = βΤ = τ / τ N = 1/N, χ = 1/N
Следовательно, логарифмический декремент затухания χ есть
физическая величина, обратная числу колебаний, по истечению
которых амплитуда А уменьшается в e раз. Если χ = 0,01,
то N = 100.
Слайд 8Где ψ = arctg(β/ω). График этой функции изображен на рис. 26.2.
Рис. 26.2.
Где ψ = arctg(β/ω). График этой функции изображен на рис. 26.2.
Рис. 26.2.

Слайд 10перестает быть периодическим. При β > ω0 корни характеристичес-
кого уравнения становятся вещественными
перестает быть периодическим. При β > ω0 корни характеристичес-
кого уравнения становятся вещественными

и решение дифферен-
циального уравнения (26.1) оказывается равным сумме двух
экспонент: х = С1е-λ1t + С2е-λ2t , где λ1= - β +iω, а λ2= - β - iω, а С1 и
С2 - вещественные константы, значения которых зависят от нача-
льных условий (от х0 и υ0). Следовательно движение носит
апериодический (непериодический) характер – выведенная из поло-
жения равновесия система возвращается в положение равновесия,
не совершая колебаний. На рис. 26.26 показано три возможных
способа возвращения системы к положению равновесия при
апериодическом движении. Каким из этих способов приходит
циального уравнения (26.1) оказывается равным сумме двух
экспонент: х = С1е-λ1t + С2е-λ2t , где λ1= - β +iω, а λ2= - β - iω, а С1 и
С2 - вещественные константы, значения которых зависят от нача-
льных условий (от х0 и υ0). Следовательно движение носит
апериодический (непериодический) характер – выведенная из поло-
жения равновесия система возвращается в положение равновесия,
не совершая колебаний. На рис. 26.26 показано три возможных
способа возвращения системы к положению равновесия при
апериодическом движении. Каким из этих способов приходит
Рис. 26.26.
Слайд 11Это условие будет выполнено в том случае, если выведенной из
положения равновесия системе
Это условие будет выполнено в том случае, если выведенной из
положения равновесия системе

сообщить достаточно сильный
толчок к положению равновесия. Если, отведя систему из
положения равновесия, отпустить ее без толчка (т.е. с υ0 = 0) или
сообщить ей толчок недостаточной силы (такой, что υ0 окажется
меньше определяемой условием (26.6)), движение будет
Происходить в соответствии с кривой А на рис. 26.26.
толчок к положению равновесия. Если, отведя систему из
положения равновесия, отпустить ее без толчка (т.е. с υ0 = 0) или
сообщить ей толчок недостаточной силы (такой, что υ0 окажется
меньше определяемой условием (26.6)), движение будет
Происходить в соответствии с кривой А на рис. 26.26.
Слайд 14Рис. 26.27.
Рис. 26.27.

- Предыдущая
Медикаментозное лечение в сестринской практикеСледующая -
Математика без границ. Конкурс







 estestvenny_sposob
estestvenny_sposob Магнитное поле и его характеристики
Магнитное поле и его характеристики Теория электромагнитного поля
Теория электромагнитного поля Сравнение АКБ. Свинцово-кислотные аккумуляторы
Сравнение АКБ. Свинцово-кислотные аккумуляторы Презентация на тему Майкл Фарадей
Презентация на тему Майкл Фарадей  Влияние наноразмерного гидрофильного наполнителя на релаксацию заряда в композитных плёнках полилактида
Влияние наноразмерного гидрофильного наполнителя на релаксацию заряда в композитных плёнках полилактида Взаимодействие нейтронов с веществом. Лекция № 06
Взаимодействие нейтронов с веществом. Лекция № 06 Структура поверхностных слоёв в твёрдых и жидких материалах
Структура поверхностных слоёв в твёрдых и жидких материалах Свет. Свойства света
Свет. Свойства света Измерение физических величин
Измерение физических величин Презентация на тему Силы в природе (7 класс)
Презентация на тему Силы в природе (7 класс)  Ультрафиоле́товое излуче́ние
Ультрафиоле́товое излуче́ние Типовой расчет №3. Молекулярная физика и термодинамика
Типовой расчет №3. Молекулярная физика и термодинамика Входные геоэлектрические модели геологических сред с наличием зоны ГРП
Входные геоэлектрические модели геологических сред с наличием зоны ГРП ГИА. 9 класс. Часть 2
ГИА. 9 класс. Часть 2 Еволюція фізичної картини світу. Фізика і науково-технічний прогрес. Урок 98
Еволюція фізичної картини світу. Фізика і науково-технічний прогрес. Урок 98 Лекция17
Лекция17 Газожидкостная хроматография (ГЖХ)
Газожидкостная хроматография (ГЖХ) Механика. Удар
Механика. Удар Система управления двигателем
Система управления двигателем Гидродинамическое моделирование
Гидродинамическое моделирование Исследователи света и цвета
Исследователи света и цвета Автоматическое управление. Типовая упрощенная структура САУ
Автоматическое управление. Типовая упрощенная структура САУ Правило буравчика. Правило правой руки
Правило буравчика. Правило правой руки Механикалық тербелістердің адамға әсері
Механикалық тербелістердің адамға әсері Презентация на тему Прямолинейное равноускоренное движение
Презентация на тему Прямолинейное равноускоренное движение  Коэффициент трения скольжения
Коэффициент трения скольжения Замена радиатора на системе охлаждения для марки ВАЗ 2107
Замена радиатора на системе охлаждения для марки ВАЗ 2107