Содержание
- 2. Атомистические и микроскопические методы Наиболее практически важными величинами, определяемыми в численных экспериментах на атомарном уровне, являются
- 3. Атомистические и микроскопические методы Наиболее практически важными величинами, определяемыми в численных экспериментах на атомарном уровне, являются
- 4. Атомистические и микроскопические методы ЗАЧЕМ ??? нам нужна полная энергия , для чего она используется ?
- 5. моментальные положения ионов являются параметрами уравнения Шредингера для электронов энергия электронной подсистемы Ee является функцией координат
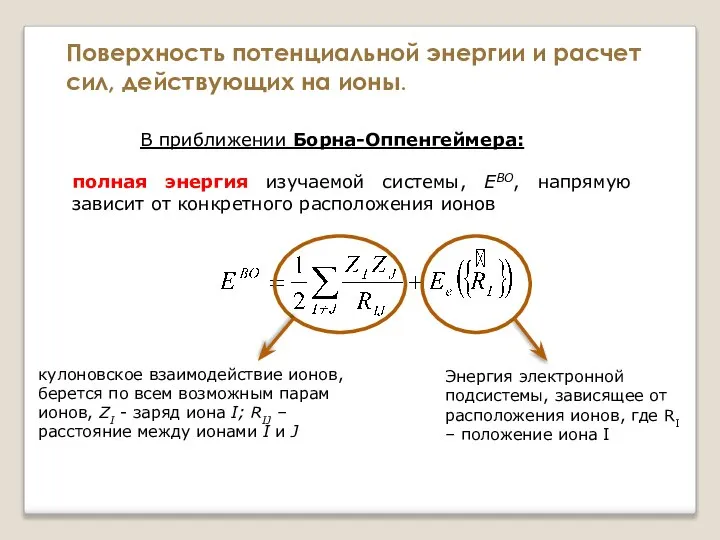
- 6. полная энергия изучаемой системы, EBO, напрямую зависит от конкретного расположения ионов Поверхность потенциальной энергии и расчет
- 7. Поверхность потенциальной энергии и расчет сил, действующих на ионы. Можно рассматривать потенциальную энергию Борна-Оппенгеймера как многомерную
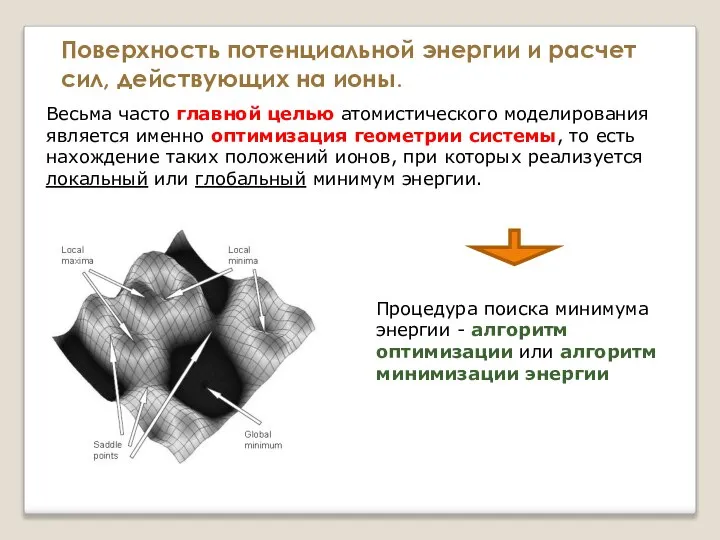
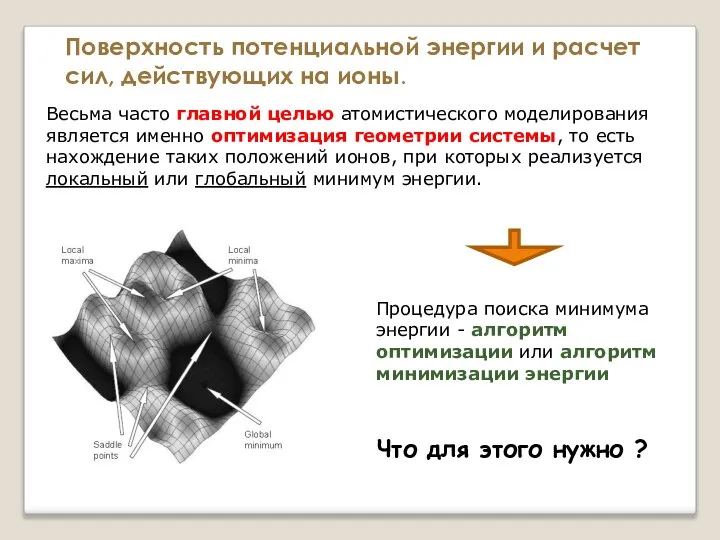
- 8. Весьма часто главной целью атомистического моделирования является именно оптимизация геометрии системы, то есть нахождение таких положений
- 9. Весьма часто главной целью атомистического моделирования является именно оптимизация геометрии системы, то есть нахождение таких положений
- 10. ! При исследовании динамического поведения ионов, а также в ряде наиболее эффективных алгоритмов минимизации энергии необходимо
- 11. Расчет сил, действующих на ионы Когда энергия задана как аналитическая функция ионных координат, ее вычисление не
- 12. Даже имея возможность рассчитывать только полные энергии, можно численно оценить силы на отдельные ионы, если придавать
- 13. Расчет сил, действующих на ионы теорема Хеллмана-Фейнмана Для вычисления такого среднего достаточно знания тех же одноэлектронных
- 14. Расчет сил, действующих на ионы теорема Хеллмана-Фейнмана силы вычисленные с помощью теоремы Хеллмана-Фейнмана очень чувствительны к
- 15. Атомистические и микроскопические методы Молекулярная статика Молекулярная динамика Главной задачей является нахождение состояния системы с минимальной
- 16. Методы молекулярной статики
- 17. Главной задачей является нахождение состояния системы с минимальной энергией (или основного состояния). Используется при исследовании :
- 18. Суть метода - математические методы минимизации для случая, когда минимизируемой функцией является полная потенциальная энергия системы.
- 19. Молекулярная статика Математическая задача минимизация функции многих переменных: Задана функция U, которая однозначно зависит от некоторого
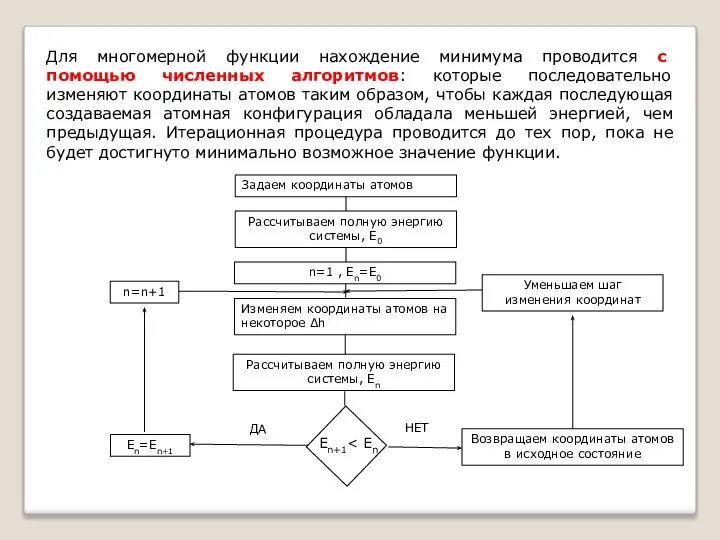
- 20. Для многомерной функции нахождение минимума проводится с помощью численных алгоритмов: которые последовательно изменяют координаты атомов таким
- 21. Молекулярная статика Алгоритмы минимизации энергии системы принято разделять на: те, которые используют производные энергии по координатам
- 22. Молекулярная статика: Методы Поиска Методы Поиска используют только значения самой функции. МИНУСЫ МЕТОДА Методы поиска, как
- 23. Молекулярная статика: Градиентные методы. В семействе Градиентных методов предполагается, что для любой точки фазового пространства возможно
- 24. Молекулярная статика: Градиентные методы. Существует целый набор методов, относящихся к семейству Градиентных методов: метод наискорейшего спуска
- 25. Молекулярная статика: Методы Ньютона . Методы Ньютона используют первые и вторые производные энергии. ПЛЮСЫ МЕТОДА Это
- 26. Молекулярная статика: Методы Ньютона . Использование производных при нахождении минимумов функций - чрезвычайно полезно, поскольку они
- 27. Молекулярная статика: Методы Ньютона . Знание направления и величины градиента энергии в любой точке позволяет выбрать
- 28. Молекулярная статика: Методы Ньютона . Вторые производные потенциальной энергии дают информацию о локальной кривизне энергетической поверхностности.
- 29. максимум - все собственные значения отрицательны, минимум - все собственные значения положительны седловая точка - некоторые
- 30. Методы первого порядка не в состоянии строго следовать дну энергетической долины, если не применяются дополнительные процедуры
- 32. Скачать презентацию
























 Химическая связь
Химическая связь Химические свойства металлов
Химические свойства металлов Влияние катализаторов на реакционную систему на примере синтеза Фишера-Тропша
Влияние катализаторов на реакционную систему на примере синтеза Фишера-Тропша Классификация углеводов: моносахариды, дисахариды, полисахариды. Химическая структура. Свойства и функция углеводов
Классификация углеводов: моносахариды, дисахариды, полисахариды. Химическая структура. Свойства и функция углеводов Соединения алифатического ряда
Соединения алифатического ряда Белки-1 2020
Белки-1 2020 Классификация веществ. Урок №7
Классификация веществ. Урок №7 Химия элементов неметаллов. Сера
Химия элементов неметаллов. Сера Металлы и их соединения. Решение экспериментальных задач
Металлы и их соединения. Решение экспериментальных задач Здравствуйте, химия! Что изучает химия
Здравствуйте, химия! Что изучает химия Реакции обмена
Реакции обмена 10-4 (2)
10-4 (2) Химическая связь и строение молекул
Химическая связь и строение молекул Сложные эфиры
Сложные эфиры Основные законы химии
Основные законы химии Энергия Гиббса
Энергия Гиббса Химия в загадках
Химия в загадках Презентация на тему В мире индикаторов - исследовательская работа
Презентация на тему В мире индикаторов - исследовательская работа  Получение и химические свойства металлов
Получение и химические свойства металлов каталитические системы на основе металлоценов и метилалюмоксана в реакциях непредельных соединений с изобутиланами
каталитические системы на основе металлоценов и метилалюмоксана в реакциях непредельных соединений с изобутиланами Презентация на тему Алканолы
Презентация на тему Алканолы  Природный источник нефть
Природный источник нефть Ковалентная связь. Электроотрицательность
Ковалентная связь. Электроотрицательность Галогены
Галогены Металлы и неметаллы
Металлы и неметаллы Презентация на тему Алюминий как химический элемент и как простое вещество
Презентация на тему Алюминий как химический элемент и как простое вещество  Химический анализ воды
Химический анализ воды Сфалерит. Кристаллическая структура
Сфалерит. Кристаллическая структура