Содержание
- 2. Задачи на смеси и сплавы Удобно решать с использованием следующих вспомогательных средств: каждая отдельная смесь (или
- 3. Например, дан раствор соли с общей массой 500 и концентрацией соли 40 %. Представляем такой раствор
- 4. ПРАВИЛО: При смешивании нескольких растворов складываются как общие массы растворов, так и массы компонентов этих растворов.
- 5. Задача. Смешали 10%- ный и 25%- ный растворы соли и получили 3кг 20% -ного раствора. Какое
- 6. Задача. Сколько кг воды нужно выпарить из 0,5 т целлюлозной массы, содержащей 85% воды, чтобы получить
- 7. Задача. Смешали 2л 60%- ного раствора соли с 3л 50%- ного раствора соли и к смеси
- 8. Задачи на «сухой остаток» Задача. В магазин привезли 100 кг клюквы, состоящей на 99% из воды.
- 9. Решение 90% 10% 22кг 22 ∙ 0,1 = (кг) 2,2 – масса свежих грибов без воды
- 10. Решить неравенство: (х-1) (х+8) 5-х ≥ 0 Решение Нули: 1 ; -8 ; 5 х Есть
- 11. «Шутливые» законы I: Увидел сумму – делай произведение II: Увидел произведение – делай сумму III: Увидел
- 12. Решить уравнение: sin2x ∙ sin6x = cosx ∙ cox3x увидел произведение – делай сумму : Решение
- 13. Решить уравнение: cos 2x + cos 3x = 1 2 2 Решение увидел квадрат – понижай
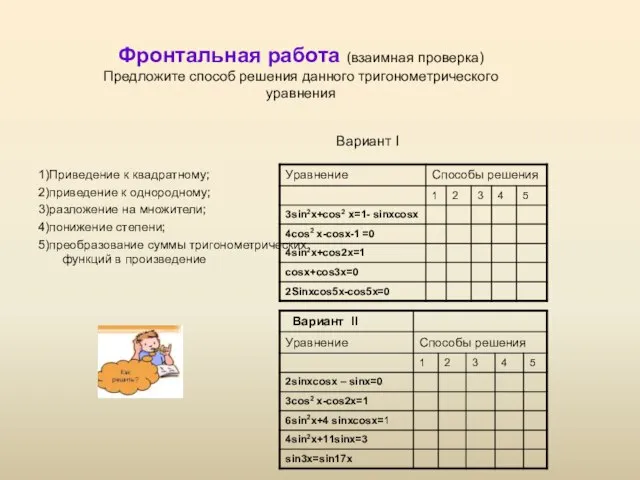
- 14. Фронтальная работа (взаимная проверка) Предложите способ решения данного тригонометрического уравнения 1)Приведение к квадратному; 2)приведение к однородному;
- 15. Проверяем Вариант I Вариант II
- 16. Экспертная работа
- 19. Метод декомпозиции Исходное неравенство О.Д.З. Декомпозиция неравенства (равносильное исходному на О.Д.З.) а f(x) - a g(x)
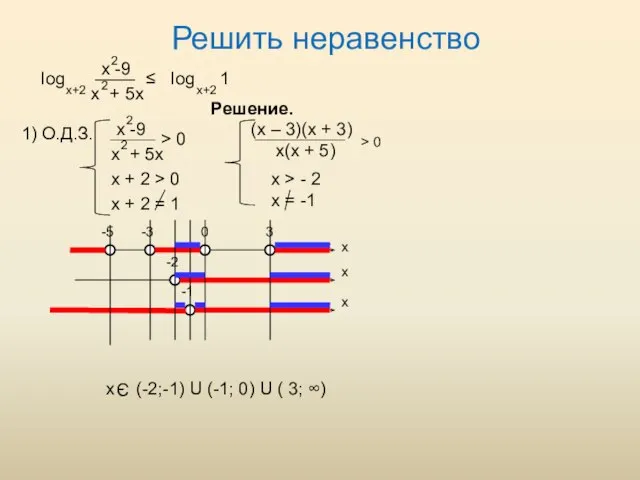
- 20. Решить неравенство 1) О.Д.З. log x -9 x + 5x 2 2 x+2 ≤ log 1
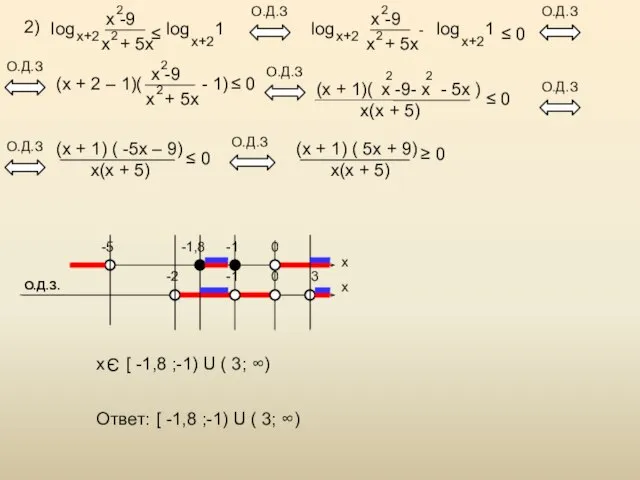
- 21. 2) log x -9 x + 5x 2 2 x+2 log 1 x+2 ≤ О.Д.З (x
- 22. Решить неравенство - (0,5) x +3x-2 2 2x +2x-1 2 x ≤ 0 Решение. 1) О.Д.З.
- 24. Скачать презентацию


















 Классификация химических элементов
Классификация химических элементов Vvedenie_v_khimiyu
Vvedenie_v_khimiyu Радиоактивные изотопы
Радиоактивные изотопы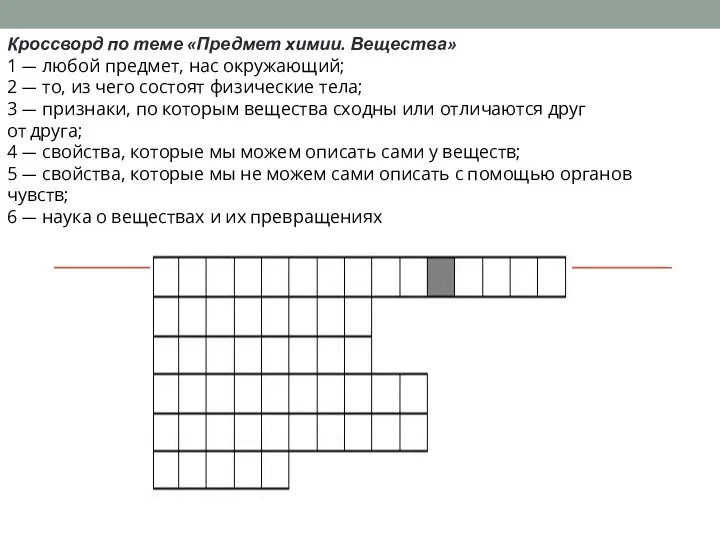 Предмет химии. Вещества
Предмет химии. Вещества Циклоалканы (циклопарафины)
Циклоалканы (циклопарафины)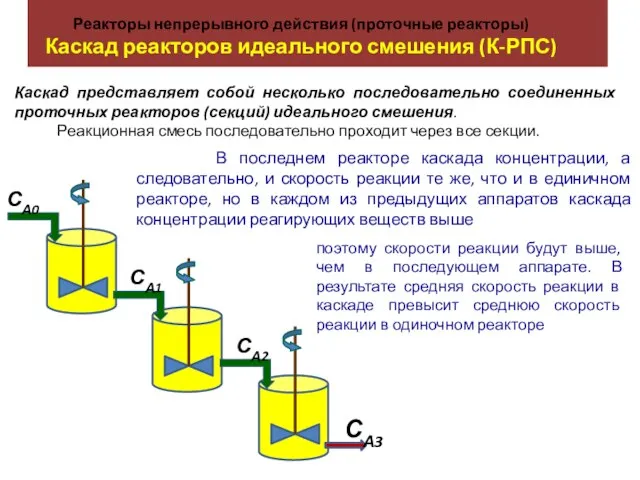 Реакторы непрерывного действия (проточные реакторы). Каскад реакторов идеального смешения (К-РПС)
Реакторы непрерывного действия (проточные реакторы). Каскад реакторов идеального смешения (К-РПС) Практикум по химии и технологии нефти и газа
Практикум по химии и технологии нефти и газа Изомерия
Изомерия Французский физик, химик, металловед 1850 - 1936
Французский физик, химик, металловед 1850 - 1936 Конструкционные и функциональные материалы: конструкционные материалы. Введение
Конструкционные и функциональные материалы: конструкционные материалы. Введение Строение атома
Строение атома Химия. Зачем она нужна? Дистанционный конкурс «Химия без лаборатории» Ученица 10 класса Климашина Василиса, ГОУСОШ № 464 – ЦАО, г. М
Химия. Зачем она нужна? Дистанционный конкурс «Химия без лаборатории» Ученица 10 класса Климашина Василиса, ГОУСОШ № 464 – ЦАО, г. М Строение атома. Распределение электронов
Строение атома. Распределение электронов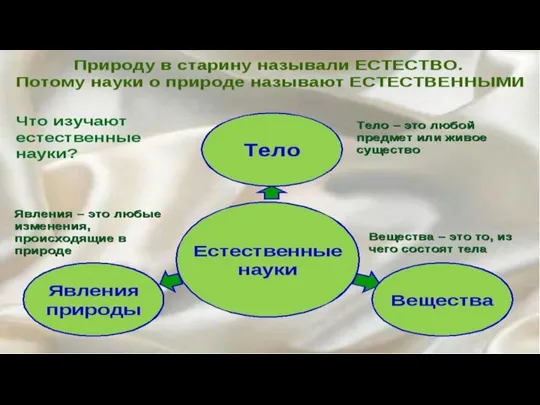 Вещество. Простые и сложные вещества
Вещество. Простые и сложные вещества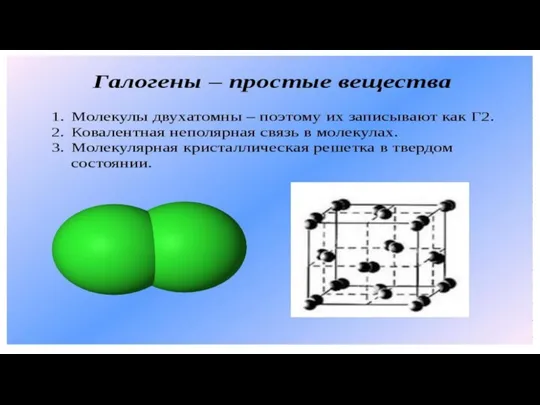 Галогены - простые вещества
Галогены - простые вещества Растворы полимеров
Растворы полимеров Уксусная кислота
Уксусная кислота Фарфор и фаянс
Фарфор и фаянс Железо и его соединения
Железо и его соединения Температурная зависимость времени спин-решеточной релаксации протонов в H2La2Ti3O10
Температурная зависимость времени спин-решеточной релаксации протонов в H2La2Ti3O10 Молярный объем газов
Молярный объем газов Полимеры
Полимеры Основы материаловедения. Раздел 1
Основы материаловедения. Раздел 1 Алкадиены. Каучук. История открытия каучука
Алкадиены. Каучук. История открытия каучука Обобщение и подготовка к химии 8 класс
Обобщение и подготовка к химии 8 класс Тест по теме Альдегиды и кетоны
Тест по теме Альдегиды и кетоны Свойства веществ
Свойства веществ Конденсированные гетероциклы. Нуклеотиды. Нуклеиновые кислоты
Конденсированные гетероциклы. Нуклеотиды. Нуклеиновые кислоты