Растворы. Часть 2

Давление пара над раствором нелетучего вещества в каком-либо растворителе всегда ниже, чем над чистым растворителем при одной и той же температуре. Это явление было открыто французским ученым Раулем и сформулировано в виде закона.
8. Понижение давления пара растворителя над раствором. Закон Рауля
Франсуа Мари Рауль
(1830-1901)

Пусть в равновесную систему жидкость А – пар А введено некоторое вещество В. При образовании раствора мольная доля растворителя XА становится меньше единицы; равновесие в соответствии с принципом Ле Шателье смещается в сторону конденсации вещества А, т.е. в сторону уменьшения давления насыщенного пара. Очевидно, что, чем меньше мольная доля компонента А в растворе, тем меньше парциальное давление его насыщенных паров над раствором.

Р = Р0∙ χ ,
где Р – давление насыщенного пара растворителя над раствором;
Р0 – давление насыщенного пара над чистым растворителем;
χ - мольная доля растворителя в растворе.
Этот закон справедлив для разбавленных (идеальных) растворов.
Закон Рауля: давление пара над раствором нелетучего вещества при постоянной температуре пропорционально мольной доле растворителя в растворе:
(12)

9. Свойства идеальных и реальных растворов. Давление насыщенного пара над идеальными растворами
Идеальные растворы. Если раствор идеальный, то он обладает следующими свойствами:
- отсутствие химического взаимодействия между молекулами;
- компоненты раствора схожи по свойствам и по строению молекул;
- образование растворов не сопровождается ни тепловым эффектов, ни изменением объема;
- силы взаимодействия между однородными частицами раствора, такие же как и между разнородными.

Если раствор состоит из двух летучих компонентов А и В, то в пар переходит как одна, так и другая жидкость.
Если раствор идеальный, то для таких растворов закон Рауля справедлив по отношению к любому из компонентов, т. е. давление пара любого из компонентом идеального раствора над жидкостью пропорционально мольной доле соответствующего компонента в растворе:
(13)

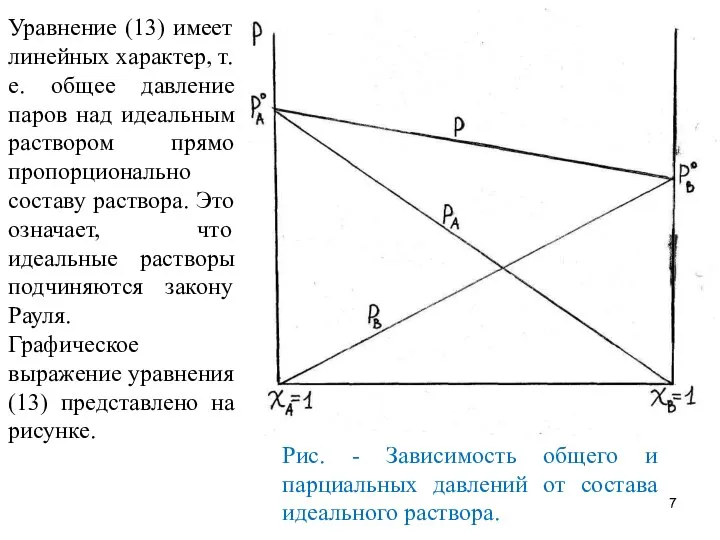
Уравнение (13) имеет линейных характер, т. е. общее давление паров над идеальным раствором прямо пропорционально составу раствора. Это означает, что идеальные растворы подчиняются закону Рауля.
Графическое выражение уравнения (13) представлено на рисунке.

10. Давление насыщенного пара над реальными растворами. Отклонения от закона Рауля
Отклонения кривых Р = f (Х) от линейной зависимости в сторону больших значений, чем рассчитанные по закону Рауля, называют положительным отклонением, а в сторону меньших значений - отрицательным.

Положительное отклонение от закона Рауля наблюдается в растворах, если силы взаимодействия между однородными частицами больше, чем между разнородными:
(А-А, В-В) > (А-В),
что облегчает переход молекул из жидкой фазы в газообразную (по сравнению с чистым растворителем). Поэтому общее давление пара оказывается большим, чем рассчитанное по закону Рауля.

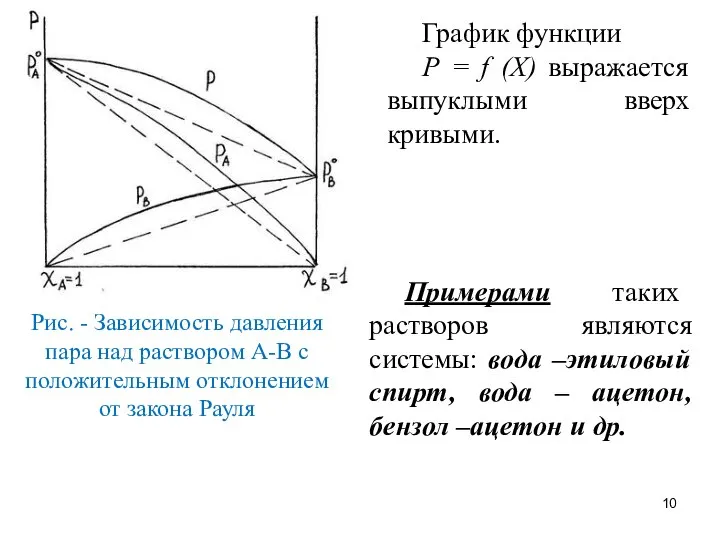
График функции
Р = f (Х) выражается выпуклыми вверх кривыми.
Примерами таких растворов являются системы: вода –этиловый спирт, вода – ацетон, бензол –ацетон и др.
Рис. - Зависимость давления пара над раствором А-В с положительным отклонением от закона Рауля

Отрицательное отклонение от закона Рауля наблюдается в растворах, если силы взаимодействия между однородными частицами меньше, чем между однородными:
(А-А, В-В) < (А-В).
Это затрудняет процесс испарения, и давление пара оказывается меньшим, чем вычисленное по закону Рауля.

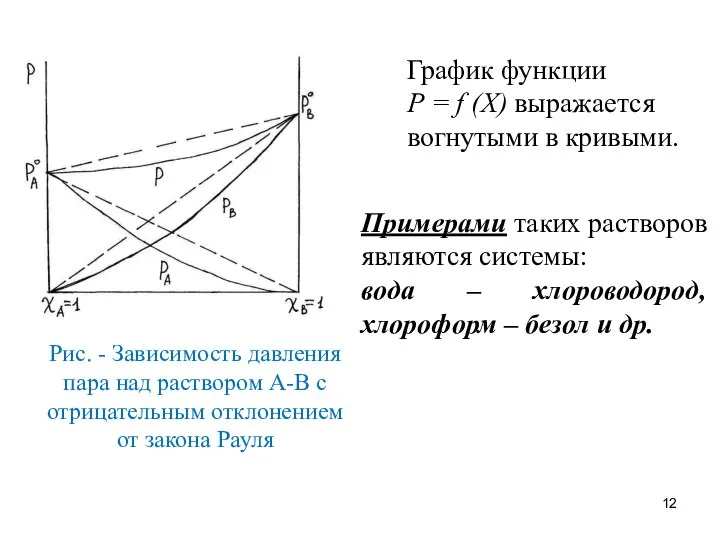
Рис. - Зависимость давления пара над раствором А-В с отрицательным отклонением от закона Рауля
График функции
Р = f (Х) выражается вогнутыми в кривыми.
Примерами таких растворов являются системы:
вода – хлороводород, хлороформ – безол и др.

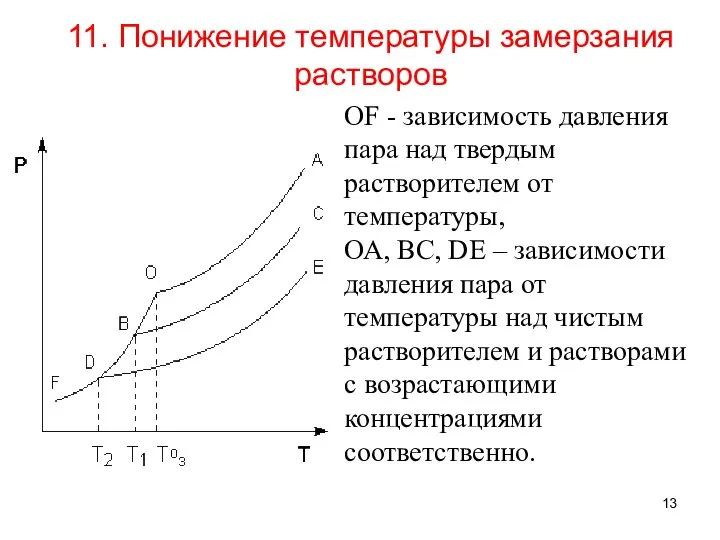
11. Понижение температуры замерзания растворов
ОF - зависимость давления пара над твердым растворителем от температуры,
ОА, ВС, DE – зависимости давления пара от температуры над чистым растворителем и растворами с возрастающими концентрациями соответственно.

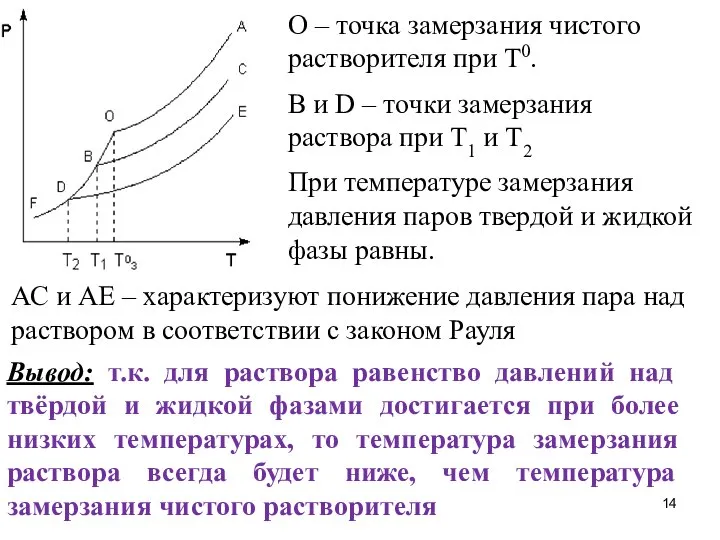
О – точка замерзания чистого растворителя при Т0.
B и D – точки замерзания раствора при Т1 и Т2
При температуре замерзания давления паров твердой и жидкой фазы равны.
АС и АЕ – характеризуют понижение давления пара над раствором в соответствии с законом Рауля
Вывод: т.к. для раствора равенство давлений над твёрдой и жидкой фазами достигается при более низких температурах, то температура замерзания раствора всегда будет ниже, чем температура замерзания чистого растворителя

Понижение температуры замерзания растворов прямо пропорционально моляльной концентрации Сm растворенного вещества:
ΔТзам. = К Сm
или
ΔТзам. =
где
К – криоскопическая постоянная; постоянна для данного растворителя и не зависит от природы растворенного вещества;
g – масса растворенного вещества;
G – масса растворителя;
М – молярная масса растворенного вещества.
(15)
Понижение температуры замерзания раствора ΔТз определяется как разность между температурами замерзания чистого растворителя Т0з и раствора Тз:
ΔТз = Т0з – Тз
(14)

Метод исследования, основанный на измерении понижения температуры замерзания растворов, называется криоскопическим.
Для определения молекулярной массы вещества криоскопическим методом пользуются формулой:
М =
(16)

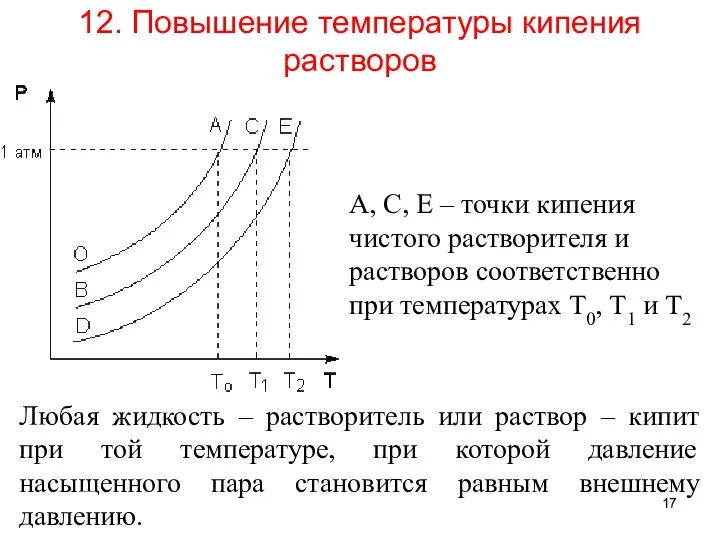
12. Повышение температуры кипения растворов
Любая жидкость – растворитель или раствор – кипит при той температуре, при которой давление насыщенного пара становится равным внешнему давлению.
А, С, Е – точки кипения чистого растворителя и растворов соответственно при температурах Т0, Т1 и Т2

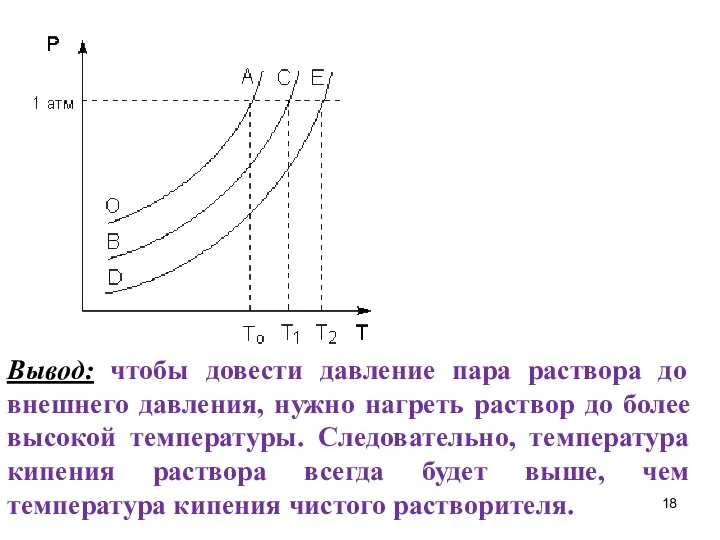
Вывод: чтобы довести давление пара раствора до внешнего давления, нужно нагреть раствор до более высокой температуры. Следовательно, температура кипения раствора всегда будет выше, чем температура кипения чистого растворителя.

Повышение температуры кипения раствора прямо пропорционально моляльной концентрации растворенного вещества:
ΔТкип.= Э Сm
или ΔТкип =
где Э – эбулиоскопическая постоянная; постоянна для данного растворителя и не зависит от природы растворенного вещества.
Повышение температуры кипения раствора ΔТк представляет собой разность между температурой кипения раствора Тк и растворителя Т0к:
ΔТк = Тк – Т0к.
(17)
(18)

Метод исследования, основанный на измерении повышения температуры кипения растворов, называется эбулиоскопическим.
М =
Для определения молекулярной массы вещества эбулиоскопическим методом пользуются формулой:
(19)

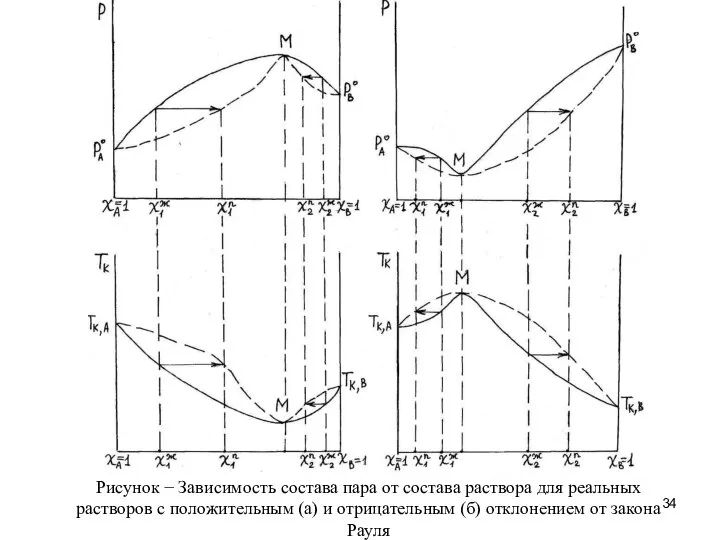
13 Состав пара над идеальным раствором. Первый закон Коновалова
Зависимость состава пара от состава раствора, состоящего из компонентов А и В описывается уравнением:
ХАп, ХВп – мольные доли компонентов А и В в паре;
ХАж, ХВж – мольные доли компонентов А и В в жидкости.
Из уравнения (20) следует, что состав пара в идеальных растворах отличается от состава жидкости, если давления над чистыми веществами не равны между собой.
(20)

Зависимость между составом пара и составом раствора описывается первым законом Коновалова: пар по сравнению с жидкостью, находящейся с ним в равновесии, относительно богаче тем компонентом, добавление которого к жидкости повышает общее давление пара, т. е. понижает температуру кипения при данном давлении.
Или проще: пар по сравнению с жидкостью обогащен наиболее летучим компонентом, т. е. компонентом, температура которого ниже, а давление насыщенного пара выше.
Уравнение (20) - математическое выражение первого закона Коновалова.
Первый закон Коновалова применим для идеальных смесей или смесей с небольшим отклонением от идеальности.

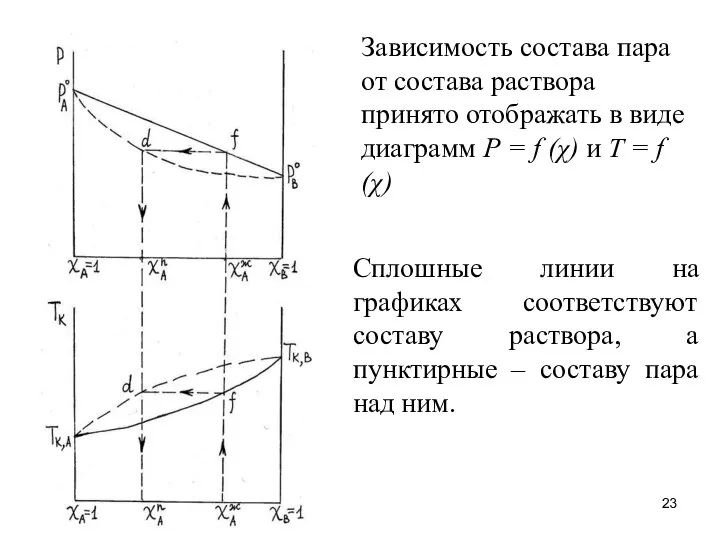
Зависимость состава пара от состава раствора принято отображать в виде диаграмм Р = f (χ) и T = f (χ)
Сплошные линии на графиках соответствуют составу раствора, а пунктирные – составу пара над ним.

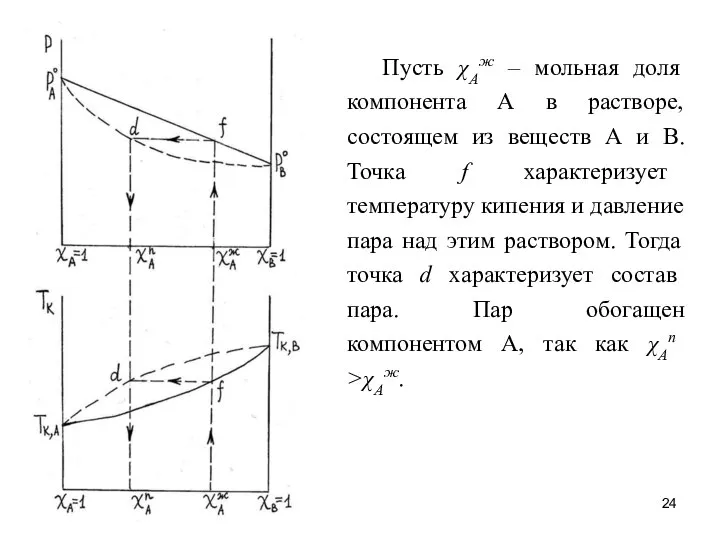
Пусть χАж – мольная доля компонента А в растворе, состоящем из веществ А и В. Точка f характеризует температуру кипения и давление пара над этим раствором. Тогда точка d характеризует состав пара. Пар обогащен компонентом А, так как χАп >χАж.

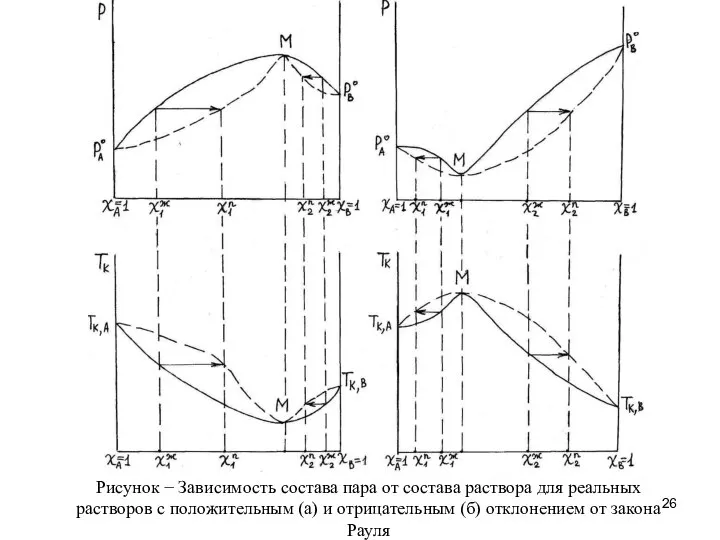
13 Состав пара над неидеальным раствором. Второй закон Коновалова
Значительные отклонения от закона Рауля в реальных растворах приводят к появлению на графиках зависимости Р = f (Х) экстремумов: максимумов – при положительном отклонении и минимумов – при отрицательных.
Такие системы подчиняются второму закону Коновалова: в точках максимума и минимума давлений паров и температур кипения составы жидкости и пара равновесной системы одинаковы.
Из чего следует вывод, что на диаграммах Р = f (Х) и
Т = f (Х) линии жидкости и пара в этих точках будут соприкасаться

Смеси, у которых парообразная и жидкая фазы находятся в равновесии при данных условиях и имеют одинаковый состав (точки М) называются азеотропными или нераздельнокипящими.

14. Перегонка растворов
Перегонка – это процесс, основанный на различии в составе пара и жидкости (т. е. на первом законе Коновалова) и предназначенный для разделения растворов на чистые компоненты путем испарения и конденсации.

Рассмотрим диаграмму Т = f (χ) для раствора А-В, свойства которого близки к идеальному.
Жидкость с мольной долей χ0 кипит при температуре Т1, при этом образуется насыщенный пар, имеющий состав (точка m) с мольной долей χ1п, более богатый содержанием компонентом А. Пар конденсируют, и конденсат снова перегоняют. Полученный при этом пар еще больше обогащен летучим компонентом А. Повторяя операцию несколько раз, можно в конденсате получить почти чистый низкокипящий компонент А. Состав жидкости по мере нагревания будет обогащаться высококипящим компонентом В.
Таким образом, осуществляется разделение смесей, близких к идеальным на практически чистые компоненты А и В. Конденсат, отобранный в определенном интервале температур, называют фракцией, а перегонку с отбором таких фракций – фракционной, или дробной, перегонкой. На практике отбор фракций и испарение проводятся в виде непрерывного процесса, называемого ректификацией.

Перегонка реальных растворов.
Если раствор является неидеальным и при этом образует азеотропную смесь, то полное разделение смеси на чистые компоненты путем обычной перегонки невозможно. При перегонке таких растворов пар может оказаться обогащенным менее летучим компонентом. Так, в случае положительного отклонения от закона Рауля (рис. а) пар над раствором состава χ1ж обогащен более летучим компонентом В, а над раствором состава χ2ж – менее летучим компонентом А. Подобное же явление наблюдается и в случае отрицательного отклонения от закона Рауля (рис. б): пар над раствором состава χ2ж обогащен более летучим компонентом В, над раствором состава χ1ж – менее летучим компонентом А.
Вывод: Реальные растворы с помощью перегонки можно разделить только на азеотропную смесь и один из компонентов.

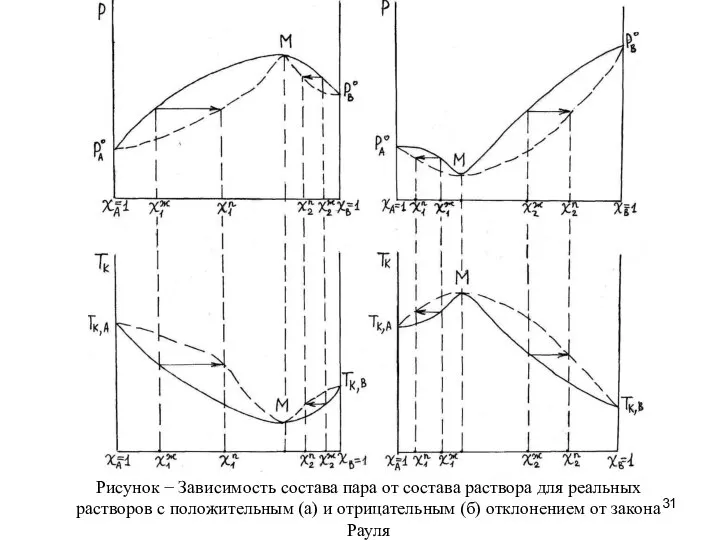
При перегонке растворов с положительным отклонением от закона Рауля состав дистиллята стремится к составу азеотропной смеси, а остаток в колбе (кубовый остаток) обогащается тем компонентом, которого в исходном растворе содержится больше, чем в азеотропной смеси.
При перегонке раствора состава χ1ж дистиллят стремится к составу азеотропной смеси М, а кубовый остаток – к компоненту А. А при перегонке раствора состава χ2ж дистиллят опять стремится к азеотропной смеси М, а кубовый остаток – к компоненту В, которого в исходном растворе больше, чем в азеотропной смеси.

При перегонке растворов с отрицательным отклонением от закона Рауля состав кубового остатка стремится к составу азеотропной смеси, а дистиллят обогащается тем компонентом, которого в исходном растворе содержится больше, чем в азеотропной смеси.
При перегонке раствора состава χ1ж кубовый остаток стремится к составу азеотропной смеси М, а дистиллят – к компоненту А. А при перегонке раствора состава χ2ж кубовый остаток опять приближается к составу азеотропной смеси М, а дистиллят – к компоненту В.

15. Осмотическое давление
Все растворы обладают способностью к диффузии.
Диффузия - это равномерное распределение вещества по всему объему раствора, протекающая по всем направлениям. Ее движущая сила – разность концентраций и стремление к максимуму энтропии.

Можно создать условие, при котором диффузия протекает только в одном направлении. Для этого раствор и растворитель разделяют полупроницаемой мембраной, через которую могут проходить только молекулы (ионы) небольшого размера.

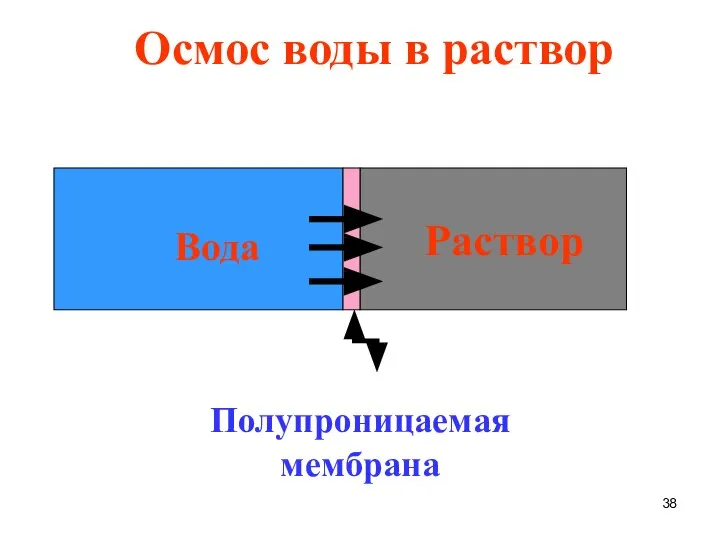
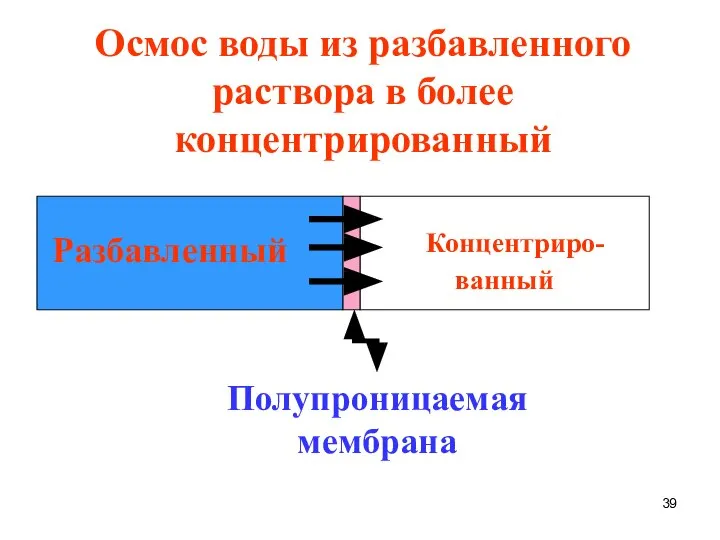
Осмос - односторонняя диффузия растворителя через полупроницаемую мембрану из растворителя в раствор или из разбавленного раствора в более концентрированный.
Процесс протекает самопроизвольно и сопровождается увеличением энтропии. Пределом его протекания является состояние равновесия.

Раствор
Вода
Полупроницаемая мембрана
Осмос воды в раствор

Концентриро-
ванный
Разбавленный
Полупроницаемая мембрана
Осмос воды из разбавленного раствора в более концентрированный

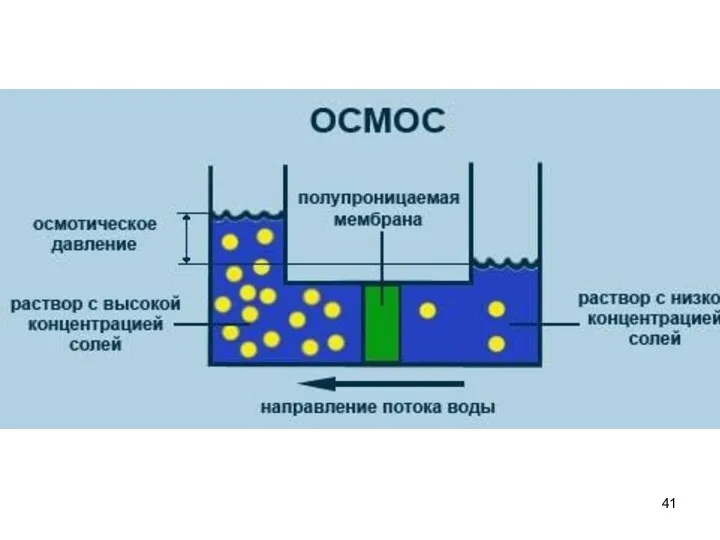
Осмотическое давление π — избыточное гидростатическое давление на раствор, отделённый от чистого растворителя полупроницаемой мембраной, при котором прекращается диффузия растворителя через мембрану (осмос). Это давление стремится уравнять концентрации обоих растворов вследствие встречной диффузии молекул растворённого вещества и растворителя.

Осмотическое давление описывается уравнением Вант- Гоффа.
Для неэлектролитов: π = С ×R×T
Для электролитов: π = i ×С ×R×T
где i — изотонический коэффициент раствора;
C — молярная концентрация раствора, выраженная через комбинацию основных единиц СИ, то есть, в моль/м³;
R — универсальная газовая постоянная;
T — термодинамическая температура раствора.
Якоб Хендрик Вант-Гофф (1852-1911)