Содержание
- 2. План лекции: реакции с участием малорастворимых электролитов, в т. ч., с малорастворимыми кислотами и основаниями. Понятие
- 3. Равновесие «осадок малорастворимого электролита – насыщенный р-р этого электролита» Рассмотрим на примере: Малорастворимый осадок PbI2 находится
- 4. Равновесие «осадок малорастворимого электролита – насыщенный р-р этого электролита» Рассмотрим на примере: Малорастворимый осадок PbI2 находится
- 5. Равновесие «осадок малорастворимого электролита – насыщенный р-р этого электролита» Вариант 1 (растворитель – чистая H2O, продолжение).
- 6. Равновесие «осадок малорастворимого электролита – насыщенный р-р этого электролита» Вариант 1 (растворитель – чистая H2O, продолжение).
- 7. Равновесие «осадок малорастворимого электролита – насыщенный р-р этого электролита» Вариант 2. Возьмем как растворитель не чистую
- 8. Равновесие «осадок малорастворимого электролита – насыщенный р-р этого электролита» Вывод: присутствие в равновесии с осадком электролита,
- 9. Равновесие «осадок малорастворимого электролита – насыщенный р-р этого электролита» Сделаем обобщение на случай равновесия с раствором
- 10. Раздел 2 в теме «Растворы» Идеальные растворы С точки зрения термодинамики различают идеальные и неидеальные (реальные)
- 11. Идеальные растворы Для конденсированных фаз взаимодействием между частицами пренебрегать нельзя, но в ряде случаев можно считать,
- 12. Идеальные растворы По аналогии со смесью идеальных газов для любых идеальных растворов должны выполняться сразу три
- 13. Идеальные растворы Для двухкомпонентной системы A – B с идеальными растворами для ΔSсм. получаем: ΔSсм. =
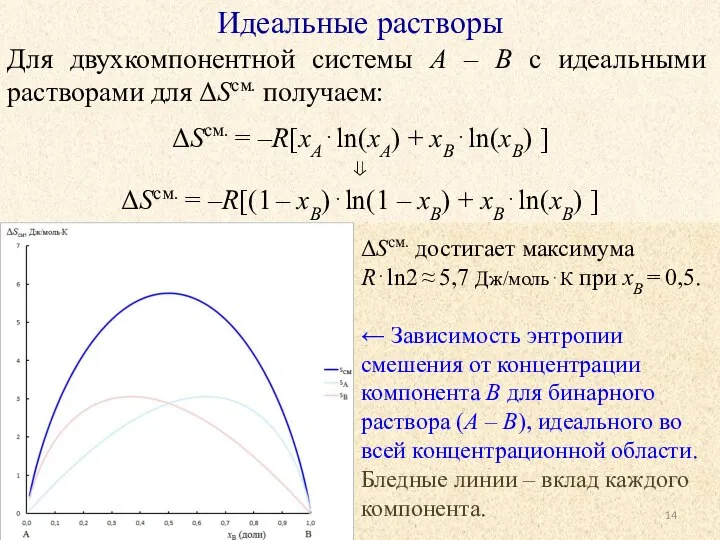
- 14. Идеальные растворы Для двухкомпонентной системы A – B с идеальными растворами для ΔSсм. получаем: ΔSсм. =
- 15. Идеальные растворы Однотипное поведение концентрационных зависимостей основных термодинамических функций для идеальных растворов подразумевает наличие у таких
- 16. Немного в сторону: температурная зависимость давления пара над конденсированными фазами Для равновесия конденсированной фазы и пара
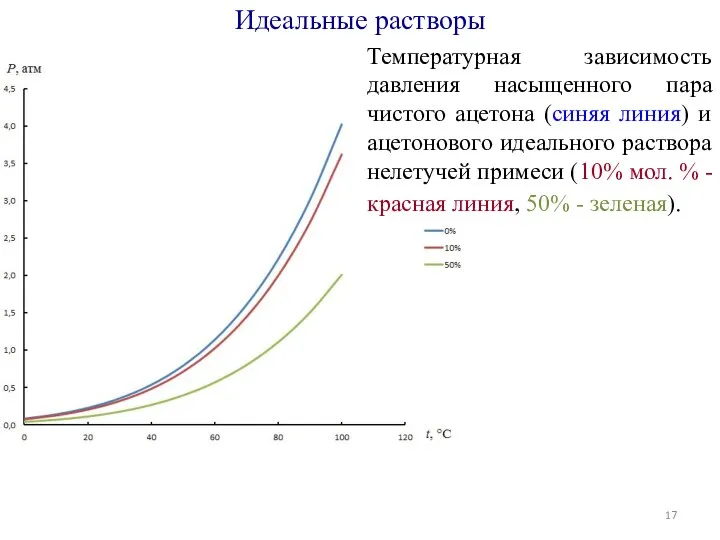
- 17. Температурная зависимость давления насыщенного пара чистого ацетона (синяя линия) и ацетонового идеального раствора нелетучей примеси (10%
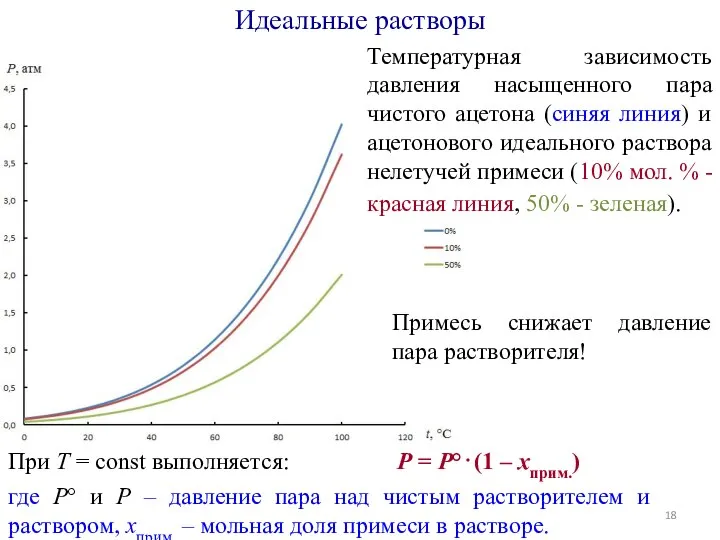
- 18. Температурная зависимость давления насыщенного пара чистого ацетона (синяя линия) и ацетонового идеального раствора нелетучей примеси (10%
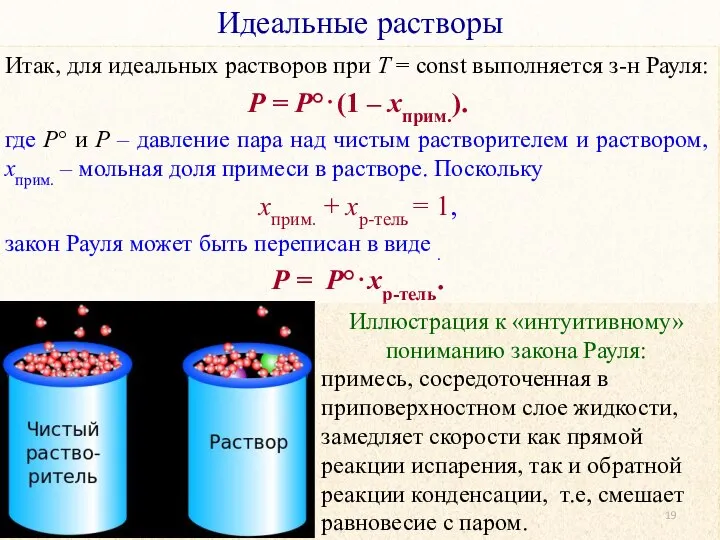
- 19. Идеальные растворы Итак, для идеальных растворов при T = const выполняется з-н Рауля: P = P°⋅(1
- 20. Идеальные растворы Итак, для идеальных растворов при T = const выполняется з-н Рауля: P = P°⋅(1
- 21. Идеальные растворы Существуют и другая форма записи и формулировки закона Рауля: Перепишем закон через содержание примеси
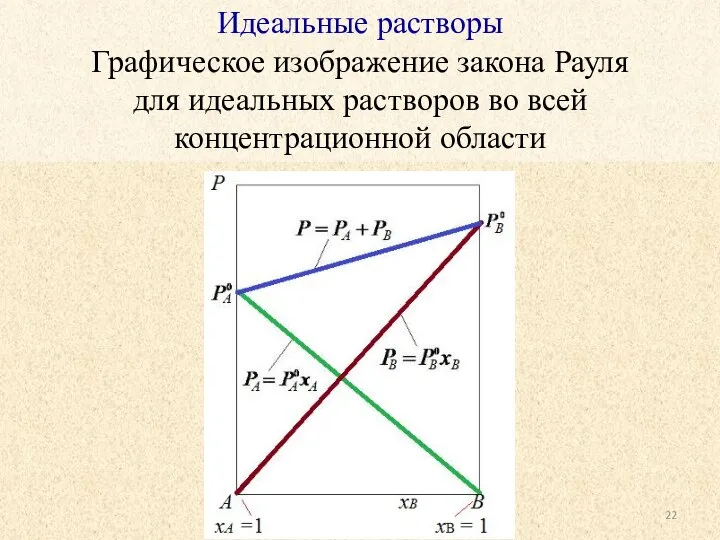
- 22. Идеальные растворы Графическое изображение закона Рауля для идеальных растворов во всей концентрационной области
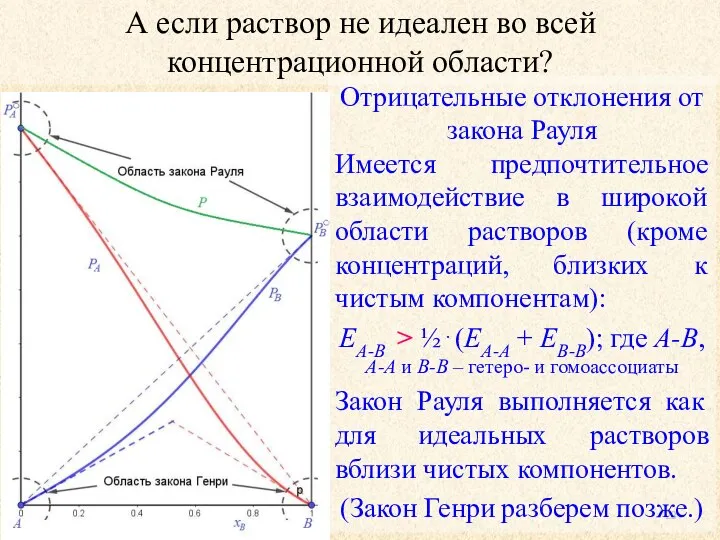
- 23. А если раствор не идеален во всей концентрационной области? Отрицательные отклонения от закона Рауля Имеется предпочтительное
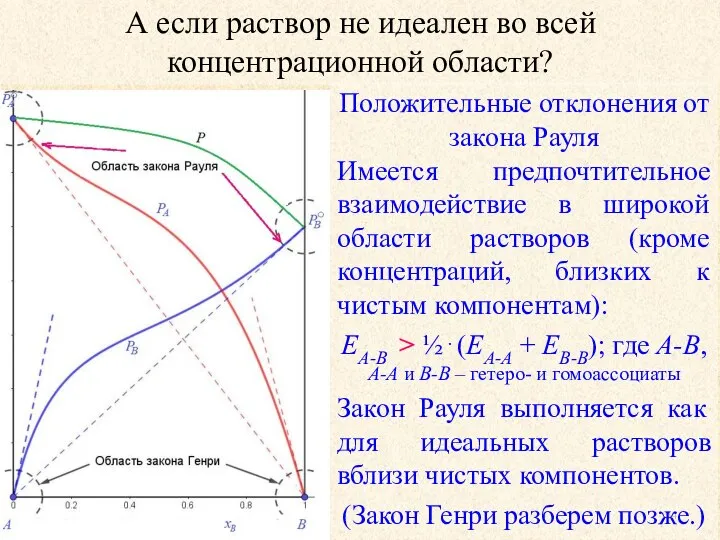
- 24. А если раствор не идеален во всей концентрационной области? Положительные отклонения от закона Рауля Имеется предпочтительное
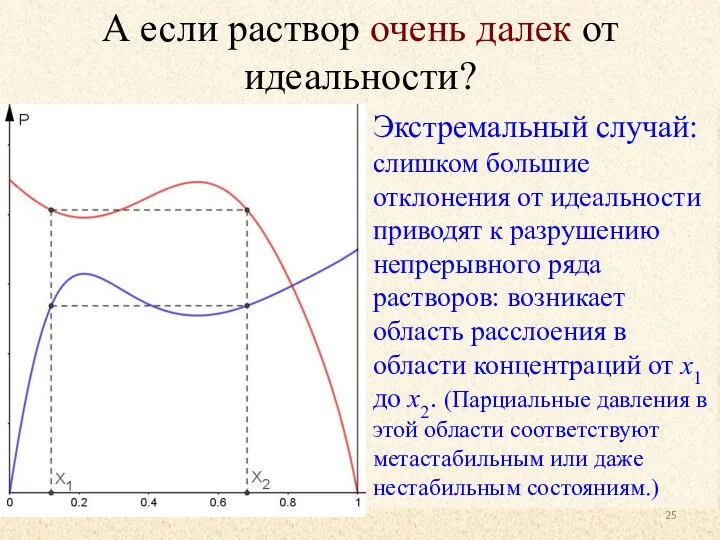
- 25. А если раствор очень далек от идеальности? Экстремальный случай: слишком большие отклонения от идеальности приводят к
- 26. Самопроизвольный направленный переход растворителя через мембрану от зоны растворителя (или разбавленного раствора) область в раствора называется
- 27. Идеальные растворы Коллигативные законы 2. Осмотический закон Вант-Гоффа Дополнительное внешнее давление P = π, которое необходимо
- 28. Осмос в природе, биологии и технике
- 29. 2. Осмотический закон Вант-Гоффа При малых концентрациях примеси xB на основании (формула разложения ln в ряд)
- 30. 2. Осмотический закон Вант-Гоффа На основании анализа сути осмоса, а также уравнения (8′) (или более упрощенного
- 32. Скачать презентацию





















 Смог як хімічне явище
Смог як хімічне явище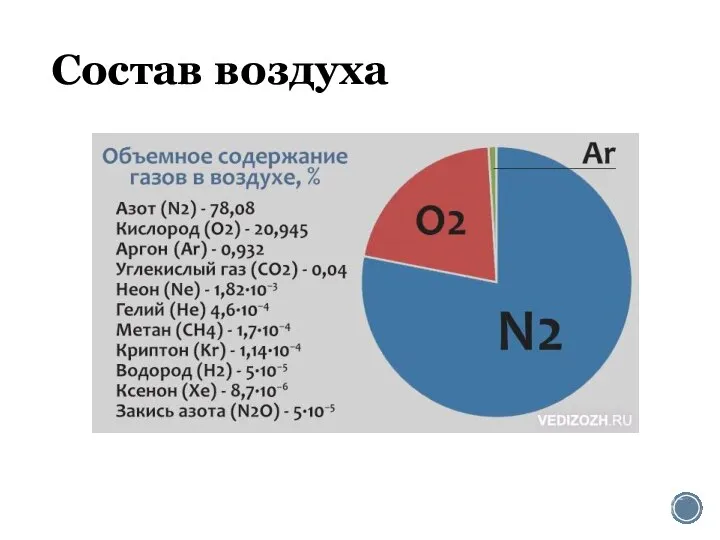 Состав воздуха. Азот
Состав воздуха. Азот Углеводороды: классификация
Углеводороды: классификация ТЭЦ, работающие на каменном угле более экологичны, чем на буром. Факт или вымысел?
ТЭЦ, работающие на каменном угле более экологичны, чем на буром. Факт или вымысел? Массовая доля химич элемента
Массовая доля химич элемента Анилин. Строение и свойства анилина
Анилин. Строение и свойства анилина Наблюдения в сходящемся свете. Коноскопия
Наблюдения в сходящемся свете. Коноскопия Современные представления о строении атома
Современные представления о строении атома Синтетические высокомолекулярные органические вещества
Синтетические высокомолекулярные органические вещества Периодическая система химических элементов. Дмитрий Иванович Менделеев
Периодическая система химических элементов. Дмитрий Иванович Менделеев Исследование растворимости в системе уксусная кислота-этиловый спирт-этилацетат-вода методом изотермического титрования при 60˚C
Исследование растворимости в системе уксусная кислота-этиловый спирт-этилацетат-вода методом изотермического титрования при 60˚C Оксид кремния
Оксид кремния Презентация на тему Теория строения органических соединений
Презентация на тему Теория строения органических соединений  Перекрывающиеся гены
Перекрывающиеся гены Сераорганические соединения
Сераорганические соединения Презентация на тему Алкины
Презентация на тему Алкины  Расчет по химическим уравнениям
Расчет по химическим уравнениям Пространственное строение углеводородов
Пространственное строение углеводородов Влияние спиртов на организм человека
Влияние спиртов на организм человека Рідкі кристали та їх властивості
Рідкі кристали та їх властивості Химическая лаборатория
Химическая лаборатория Различные варианты заданий ЕГЭ по теме Электролиз
Различные варианты заданий ЕГЭ по теме Электролиз Оловянная чума
Оловянная чума Разминка для болельщиков
Разминка для болельщиков Идеальный газ
Идеальный газ Спирты в жизни человека
Спирты в жизни человека Плавленые сыры без фосфатов
Плавленые сыры без фосфатов Разработка системы подготовки лаборанта химического анализа
Разработка системы подготовки лаборанта химического анализа