Рівняння характеристики крупності

ПЛАН ЛЕКЦІЇ
Історія розвитку питання від Годена до Розіна-Раммлера.
Вивід рівнянь Андрєєва-Годена та Розіна-Раммлера
визначення констант рівняньАндрєєва-Годена та Розіна-Раммлера. Області використання рівнянь.
Обмеження при використанні рівняння Розіна-Раммлера.

При построении суммарных характеристик в широком диапазоне крупностей зерен материала отрезки на оси абсцисс в области мелких классов получаются весьма малого размера, что затрудняет построение и использование гранулометрических характеристик. Приходится строить непомерно большие графики. Чтобы этого избежать суммарные характеристики строят в полулогарифмической или логарифмической системе координат.
Если взять логарифмическую характеристику материала "по минусу", то его гранулометрический состав можно представить уравнением
где γ − cуммарный выход класса мельче отверстий сита (по минусу);
k − коэффициент, равный тангенсу угла наклона прямой;
d − размер отверстий сита;
lgA − отрезок, отсекаемый прямой на оси ординат.

γ=Adm.
Данное уравнение суммарной характеристики называют уравнением "Годена-Андреева". Значение показателя m определяет направление и степень изгиба гранулометрической характеристики. Если характеристику построить "по плюсу", то она будет: при m>1 − выпуклой, при m<1 − вогнутой и при m=1 − прямой. Следовательно, по значению m можно судить о преобладании в материале крупных или мелких зерен.
Уравнение "Годена-Андреева" имеет смысл в промежутке от 0 до 4,5, при этом коэффициент А имеет физический смысл:
А=100/ хm

Коэффициент m в уравнении позволяет определить преобладающий кусок материала. m›1 крупный; m=1 равномерно распределен; m‹мелкий.
Задачи
Определить коэффициент А, если известно, что уравнение Гадена-Андреева имеет вид γ=Аd2, d=10 мм.
Определить выход класса -2 мм γ=5 d2

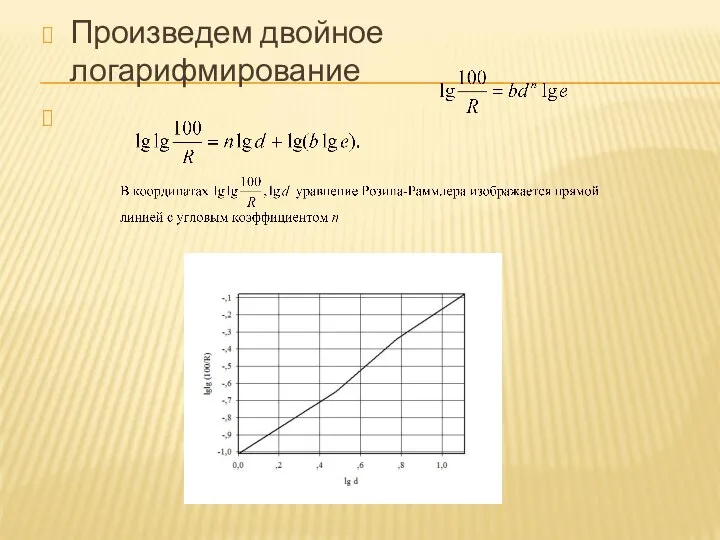
Произведем двойное логарифмирование