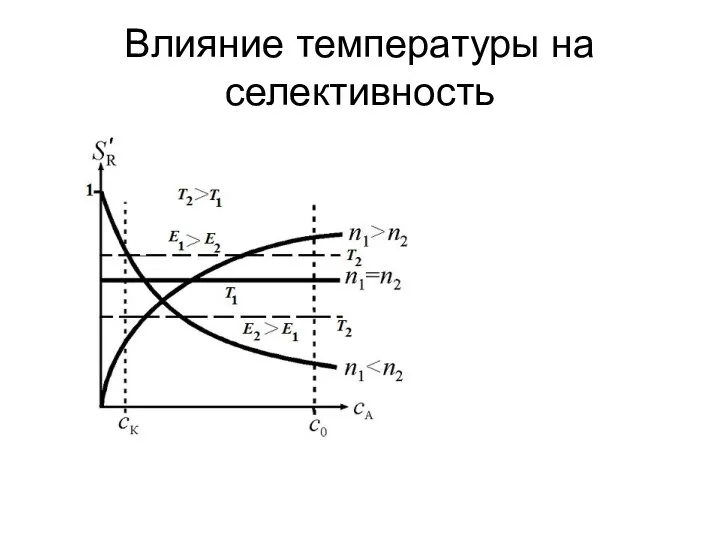
Слайд 2Влияние температуры на селективность
Слайд 3Последовательные реакции
Например, две реакции 1-го порядка:
W А= -r1 ; W R =
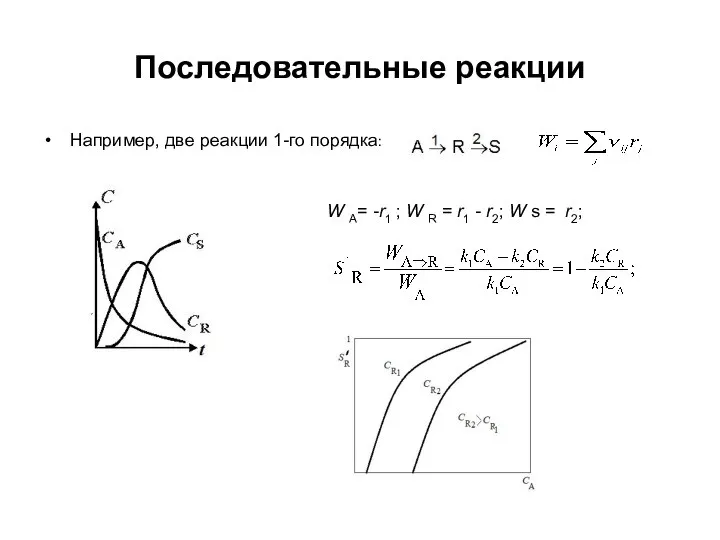
r1 - r2; W s = r2;
Слайд 4Выводы
о целесообразном режиме проведения процесса с последовательной схемой превращения
Высокую селективность процесса

по промежуточному веществу R можно получить при больших концентрациях А и малом содержании промежуточного R, т.е. при небольшой степени превращения исходного вещества.
Влияние температуры на селективность в последовательной реакции аналогично параллельной схеме превращения.
Слайд 5НЕОДНОЗНАЧНОСТЬ И МНОЖЕСТВЕННОСТЬ СТАЦИОНАРНЫХ РЕЖИМОВ В АДИАБАТИЧЕСКОМ РЕАКТОРЕ
Если в адиабатическом реакторе проводят

экзотермическую реакцию, то система уравнений материального и теплового балансов может иметь как одно, так и несколько решений.
Покажем на примере РИС-Н при протекании в нем реакции 1-го порядка. Математически процесс в РИС-Н описывается уравнениями:
откуда было получено уравнение адиабаты:
Левая часть уравнения пропорциональна теплоотводу qТ из реакционной зоны проходящим реакционным потоком и представляет собой прямолинейную зависимость от Т , правая часть – теплоподводу qр за счет протекания экзореакции и представляет собой S-образную зависимость от Т. По существу уравнение адиабаты –это уравнение теплового баланса. Решим его графически и найдем температуру Т в реакторе.
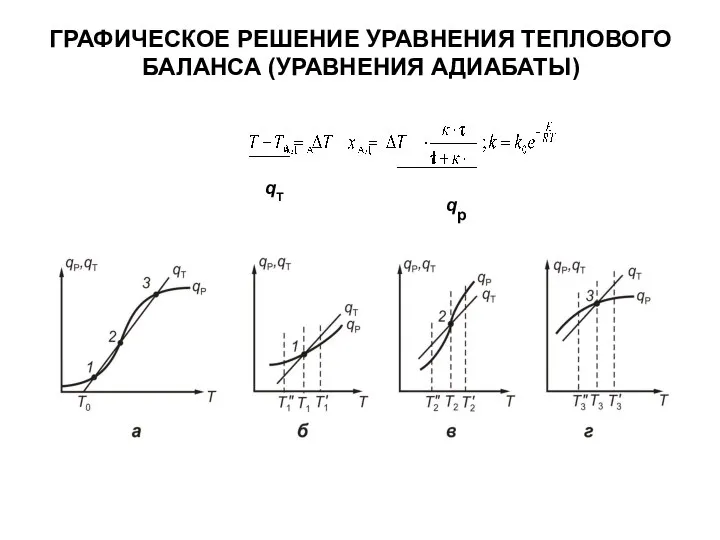
Слайд 6ГРАФИЧЕСКОЕ РЕШЕНИЕ УРАВНЕНИЯ ТЕПЛОВОГО БАЛАНСА (УРАВНЕНИЯ АДИАБАТЫ)
qT
qp
Слайд 7АНАЛИЗ РЕШЕНИЯ
Решение уравнение адиабаты имеет 1 или 3 корня (рис.) Все режимы

1, 2 или 3 – стационарные. Нелинейная зависимость между тепловыделением qp(Т) в реакторе от температуры обусловливает возможность появления неоднозначных стационарных режимов (несколько точек пересечения с линейной зависимостью qТ(Т).
В низкотемпературном режиме 1 скорость и степень превращение в реакторе – небольшие. При почти полном превращении в режиме 3 температура в реакторе будет большая, ≈равная адиабатическому разогреву. Привлекательным может оказаться среднетемпературный режим 2.
Для проверки условий его реализации рассмотрим свойства всех стационарных режимов.
Слайд 8УСТОЙЧИВОСТЬ СТАЦИОНАРНЫХ РЕЖИМОВ
Пусть процесс находится в стационарном режиме 1 (рис. б).

Температура в реакторе Т1. Пусть по каким-либо причинам температура увеличилась до Т1'. При этом qт возрастет больше, чем qp. Если источник возмущения устранен, то преобладаю-щий теплоотвод (qт) приведет к снижению температуры. Режим самопроизвольно вернется в первоначальное состояние с температурой Т1. Если температура в реакторе уменьшится до Т1", то тепловыделение qp станет больше теплоотвода qт. Реактор будет разогреваться до температуры стационарного режима Т1. Аналогичная ситуация будет и в высокотемпературном стационарном состоянии 3 (рис. г).
Такие стационарные состояния называются устойчивыми, и для них выполняется условие
dqp/dT < dqт/dT
Слайд 9В среднетемпературном режиме 2 (рис. в) повышение температурыотТ2 до Т2' из-за возможного

возмущения режима приведет к более сильному возрастанию тепловыделения qp, чем теплоотвода qт. Температура в реакторе будет продолжать увеличиваться вплоть до высокотемпературного стационарного состояния. Самопроизвольно прежний среднетемпературный режим не восстановится. Понижение температуры доТ2"приведет к дальнейшему остыванию реактора, вплоть до достижения низкотемпературного состояния. И такое будет происходить при любых малых изменениях T - первоначальный стационарный режим не будет восстанавливаться самопроизвольно. Такой режим называется неустойчивым. Для него dqp/dT > dqт/dT.
Вывод: Если в стационарное состояние внесено кратковременное возмущение, и после его снятия первоначальное состояние самопроизвольно восстановится - оно считается устойчивым.
Неустойчивое стационарное состояние самопроизвольно не восстанавливается после внесения в него кратковременных возмущений.








 Структура периодической таблицы
Структура периодической таблицы Строение атома. Распределение электронов
Строение атома. Распределение электронов Презентация на тему Химические свойства алкенов
Презентация на тему Химические свойства алкенов  Тривиальные названия
Тривиальные названия Олеиновая кислота
Олеиновая кислота Жири. Склад жирів, фізичні властивості. Природні й гідрогенізовані жири. Біологічна роль жирів
Жири. Склад жирів, фізичні властивості. Природні й гідрогенізовані жири. Біологічна роль жирів Кремний и его соединения
Кремний и его соединения Кислоты. Химический диктант. 8 класс
Кислоты. Химический диктант. 8 класс Электролитическая диссоциация
Электролитическая диссоциация Презентация по химии на тему _Высокомолекулярные Соединения_ (1)
Презентация по химии на тему _Высокомолекулярные Соединения_ (1) α-карбин и β-карбин
α-карбин и β-карбин Сера и её соединения
Сера и её соединения Разработка системы подготовки лаборанта химического анализа
Разработка системы подготовки лаборанта химического анализа Химия природная и синтетическая: за и против
Химия природная и синтетическая: за и против Физические свойства элементов 2 (ІІ) - группы
Физические свойства элементов 2 (ІІ) - группы Вдоль по радуге
Вдоль по радуге Классификация реакций. Таблица
Классификация реакций. Таблица Пиримидин (шестичленный гетероцикл с двумя атомами азота)
Пиримидин (шестичленный гетероцикл с двумя атомами азота) Три службы Менделеева для России
Три службы Менделеева для России Учебная дисциплина Естествознание. Раздел II. Химия
Учебная дисциплина Естествознание. Раздел II. Химия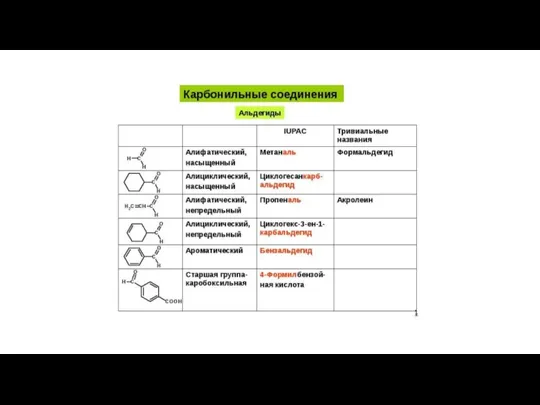 Карбонильные соединения (альдегиды)
Карбонильные соединения (альдегиды) Липиды. Функции липидов
Липиды. Функции липидов Моносахариды
Моносахариды Презентация учителя химии, биологии и экологии МОУ СОШ п.Алексеевка Бешагина Владимира Викторовича
Презентация учителя химии, биологии и экологии МОУ СОШ п.Алексеевка Бешагина Владимира Викторовича Indikatori. R. Boila eksperiments
Indikatori. R. Boila eksperiments Презентация на тему Химические свойства многоатомных спиртов
Презентация на тему Химические свойства многоатомных спиртов  Техника безопасности (3)
Техника безопасности (3) Технология переработки редкоземельного сырья
Технология переработки редкоземельного сырья