10u-2a_Кодирование-I

Кодирование информации
§ 4. Дискретное кодирование

Вспомним известное
Кодирование — это представление информации в форме, удобной для её хранения, передачи и автоматической обработки.
Код — это правило, по которому сообщение преобразуется в цепочку знаков.
Язык — это система знаков и правил, используемая для записи и передачи информации.
Формальный язык — это язык, в котором однозначно определяется значение каждого слова, а также правила построения предложений и придания им смысла.

Знаковые системы
Знак — это «заменитель» объекта, вызывает в сознании объект.
– пиктограмма
Символ — это знак, о значении которого люди договорились.
§ – параграф – рубль
Знаковая система определяется алфавитом (набором используемых знаков) и правилами выполнения операций с этими знаками.
010101

Аналоговые сигналы и устройства
Аналоговый сигнал — это сигнал, который в любой момент времени может принимать любые значения в заданном диапазоне.
Аналоговые компьютеры
невозможно «очистить» сигнал от помех
при измерении сигнала вносится ошибка
при копировании аналоговая информация искажается

Дискретные (цифровые) сигналы
Дискретный сигнал — это последовательность значений, каждое из которых принадлежит некоторому конечному множеству.
Свойства:
сигнал изменяется только в отдельные моменты времени (дискретность по времени);
принимают только несколько возможных значений (дискретность по уровню).

Дискретность
Цель – максимально точно передавать сообщения при сильных помехах.
Pacta sunt servanda.
•— — •— ••• •—•—
01000011001
… закодированную с помощью конечного количества знаков некоторого алфавита.

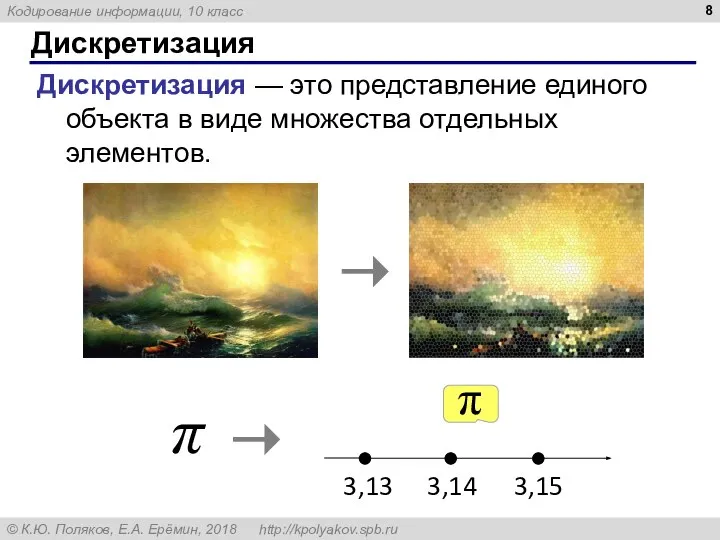
Дискретизация
Дискретизация — это представление единого объекта в виде множества отдельных элементов.
π

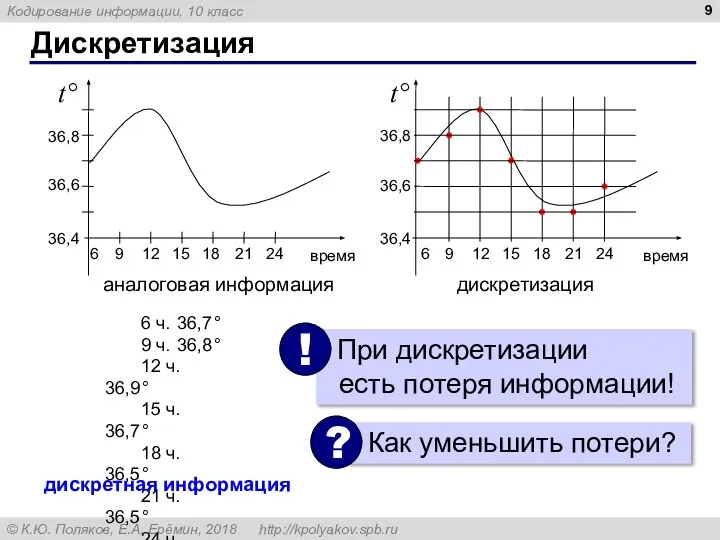
Дискретизация
6 ч. 36,7°
9 ч. 36,8°
12 ч. 36,9°
15 ч. 36,7°
18 ч. 36,5°
21 ч. 36,5°
24 ч. 36,6°
дискретная информация

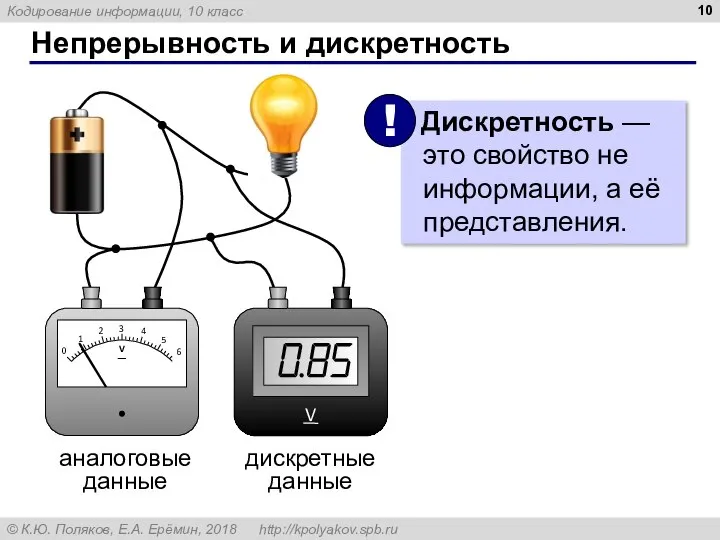
Непрерывность и дискретность
аналоговые
данные
дискретные
данные

Непрерывность и дискретность

Кодирование информации
§ 5. Равномерное и неравномерное кодирование

Вспомним известное
Алфавит — это набор знаков, который используется в языке.
Мощность алфавита — это количество знаков в алфавите.
Равномерный код — это код, в котором все кодовые слова имеют одинаковую длину.
Неравномерный код — это код, в котором кодовые слова имеют различную длину.
Двоичное кодирование — это кодирование с помощью двух знаков.
1 бит — это одна двоичная цифра (один знак сообщения, записанного в двоичном коде).

Количество возможных сообщений
Если алфавит языка состоит из M символов (имеет мощность M), количество различных сообщений длиной L знаков равно
N = M L
Сколько
возможных 7-битовых двоичных кодов?
возможных 5-буквенных слов в русском языке?
возможных 3-буквенных слов в английском языке?
335
263
Для двоичного кода: N = 2L
27

Количество возможных сообщений
Сколько
различных чисел можно закодировать в
8-битовой ячейке?
различных чисел можно закодировать в
8-разрядной ячейке троичного компьютера (-1, 0, 1)?
сколько битов нужно выделить для хранения номера спортсмена от 1 до 1000?
512 = 29 < 1000 ≤ 210 = 1024
сколько битов нужно выделить для хранения температуры от –50° до 80°?
128 = 27 < 131 ≤ 28 = 256
10
8
28
38

Правило умножения
Если в сообщении длиной L на позиции i может стоять один из Mi символов, количество различных сообщений равно
N = M1⋅ M2⋅ …⋅ ML
Задача 1. Сколько существует различных сообщений длины 5 в алфавите {A, B, C, Х}, если буква «Х» может появляться только на первом или на последнем месте?
4
4
3
3
3
M1
M5
M2
M3
M4
4 ∙ 3 ∙ 3 ∙ 3 ∙ 4 = 432

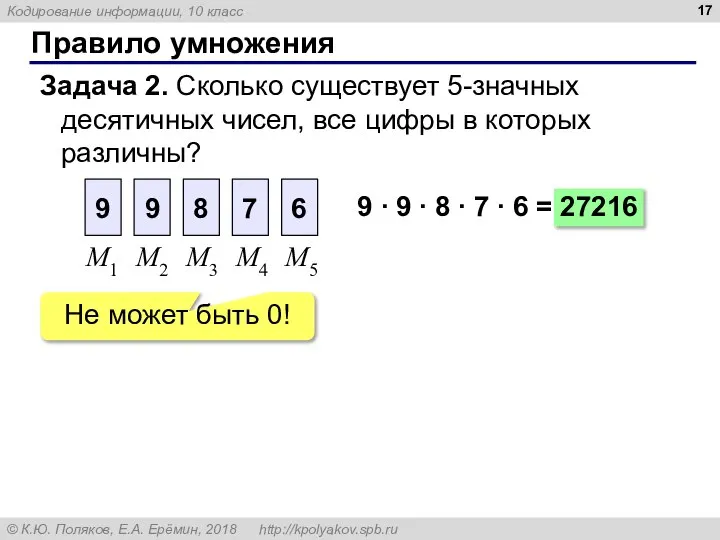
Правило умножения
Задача 2. Сколько существует 5-значных десятичных чисел, все цифры в которых различны?
9
6
9
8
7
M1
M5
M2
M3
M4
9 ∙ 9 ∙ 8 ∙ 7 ∙ 6 = 27216
Не может быть 0!

Неравномерные коды
можно уменьшить длину закодированного сообщения
не всегда однозначно декодируется
ГАГАРА
→ 010001001000
Равномерный код:
ГАГАРА
→ 010010100
Неравномерный код:
12 бит
9 бит
010010100
→ 010010100
→ 010010100
ГАГАРА
АРАРРА

Правило сложения
Задача 3. Сколько существует двоичных кодов длиной от 2 до 5 битов?
L = 2: N2 = 22 = 4
L = 3: N3 = 23 = 8
L = 4: N4 = 24 = 16
L = 5: N5 = 25 = 32

Правила умножения и сложения
Задача 4. Сколько существует различных
3-буквенных слов в алфавите {К, Р, О, Т}, в которых буква К встречается ровно 1 раз?
К
*
*
1 ∙ 3 ∙ 3 = 9
1
3
3
К
*
*
3 ∙ 1 ∙ 3 = 9
К
*
*
3 ∙ 3 ∙ 1 = 9
9 + 9 + 9 = 27

Задачи
Сколько существует в коде Морзе различных последовательностей из точек и тире, длина которых от 4 до 6 символов?
Вася и Петя передают друг другу сообщения, используя синий, красный и зелёный фонарики. Это они делают, включая по одному фонарику на одинаковое короткое время в некоторой последовательности. Количество вспышек в одном сообщении — 3 или 4, между сообщениями — паузы. Сколько различных сообщений могут передавать мальчики?

Задачи
Шахматная доска состоит из 8 столбцов и 8 строк. Какое минимальное количество битов потребуется для кодирования координат одной шахматной фигуры?
Для кодирования значений температуры воздуха (целое число в интервале от –50 до 40) используется двоичный код. Какова минимальная длина двоичного кода?
Дорожный светофор подаёт шесть видов сигналов (непрерывные красный, жёлтый и зелёный, мигающие жёлтый и зелёный, мигающие красный и жёлтый одновременно). Подряд записано 100 сигналов светофора. Определите информационный объём этого сообщения в битах.

Задачи
Автомобильный номер длиной 6 символов составляется из заглавных букв (всего используется 12 букв) и десятичных цифр в любом порядке. Каждый символ кодируется одинаковым и минимально возможным количеством битов, а каждый номер — одинаковым и минимально возможным количеством байтов. Определите объём памяти, необходимый для хранения 32 автомобильных номеров.

Кодирование информации
§ 6. Декодирование

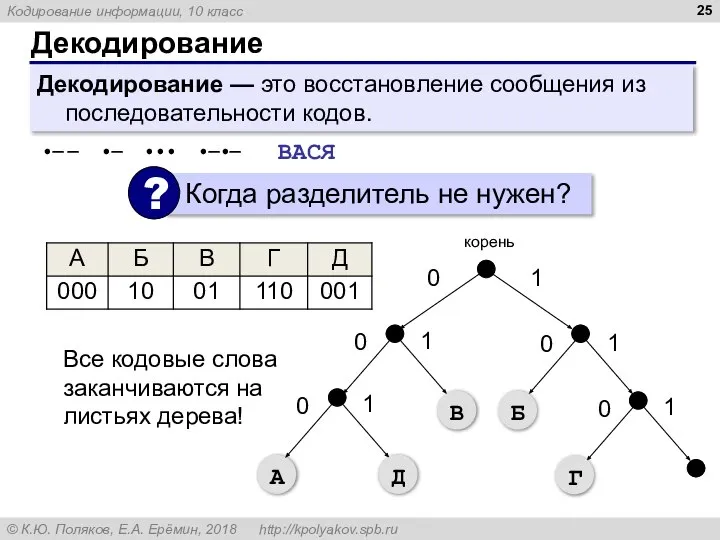
Декодирование
Декодирование — это восстановление сообщения из последовательности кодов.
•— — •— ••• •—•—
ВАСЯ
Все кодовые слова заканчиваются на листьях дерева!

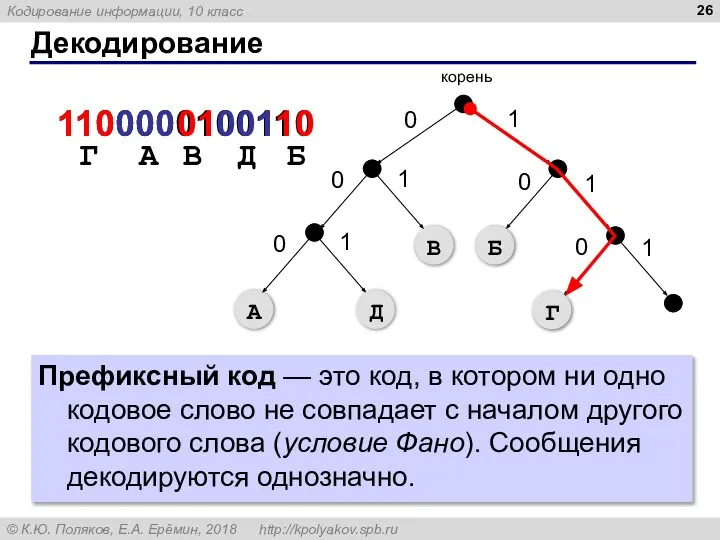
Декодирование
1100000100110
110
Г
000
01
001
10
А
В
Д
Б
Префиксный код — это код, в котором ни одно кодовое слово не совпадает с началом другого кодового слова (условие Фано). Сообщения декодируются однозначно.

Задачи
Для передачи сообщения, состоящего только из букв А, Б, В, Г, решили использовать неравномерный код:
A = 0, Б = 10, В = 110.
Как нужно закодировать букву Г, чтобы длина кода была минимальной и допускалось однозначное декодирование?
Для передачи сообщения, состоящего только из букв А, Б, В, Г, решили использовать неравномерный код:
A = 0, Б = 100, В = 101.
Как нужно закодировать букву Г, чтобы длина кода была минимальной и допускалось однозначное декодирование?

Постфиксные коды
Постфиксный код — это код, в котором ни одно кодовое слово не совпадает с окончанием другого кодового слова. Сообщения декодируются однозначно (с конца!).
011000110110
10
01
011
100
01
Б
Д
Г
Б
В

Неоднозначное декодирование
АБАГД
АБВГА
010100111101
Декодирование может быть неоднозначным…

Задача
*Докажите, что все сообщения, закодированные этим кодом, декодируются однозначно.
01000011001011110000100

Кодирование информации
§ 7. Алфавитный подход к измерению количества информации

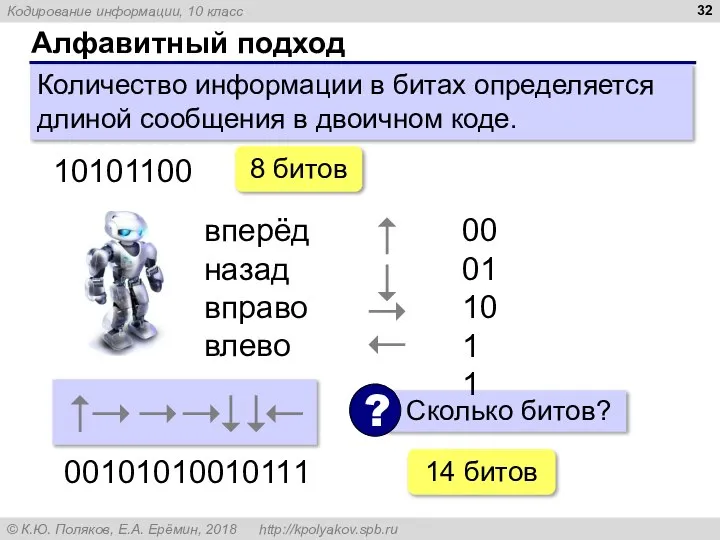
Алфавитный подход
Количество информации в битах определяется длиной сообщения в двоичном коде.
10101100
8 битов
вперёд
назад
вправо
влево
00
01
10
11
00101010010111
14 битов

Другие единицы измерения
1 байт (bytе) = 8 бит
1 Кбайт (килобайт) = 1024 байта
1 Мбайт (мегабайт) = 1024 Кбайт
1 Гбайт (гигабайт) = 1024 Мбайт
1 Тбайт (терабайт) = 1024 Гбайт
1 Пбайт (петабайт) = 1024 Тбайт
210

Алфавитный подход
определяем мощность алфавита M;
определяем количество битов информации i, приходящихся на один символ, — информационную ёмкость (объём) символа:
количество информации в сообщении:
где L – количество символов в сообщении.
I = L·i

Алфавитный подход
каждый символ несёт одинаковое количество информации
частота появления разных символов (и сочетаний символов) не учитывается
количество информации определяется только длиной сообщения и мощностью алфавита
смысл сообщения не учитывается

Задача
Определить количество информации в 10 страницах текста (на каждой странице 32 строки по 64 символа) при использовании алфавита из 256 символов.
информационная ёмкость символа:
256 = 28 ⇒ i = 8 бит = 1 байт
количество символов на странице:
32·64 = 25 ·26 = 211
общее количество символов:
L = 10·211
информационный объём сообщения:
I = L·i = 10·211·1 байтов = 20 Кбайт

Задача
Пароль длиной не более 11 символов (цифры и 12 различных букв, как строчные, так и прописные. Посимвольное равномерное кодирование, для хранения пароля отводится минимально возможное целое количество байт. Сколько байт нужно для 60 паролей?
мощность алфавита M = 10 + 12 + 12 = 34
информационная ёмкость символа:
25 < 34 ≤ 26 ⇒ i = 6 бит
на один пароль:
6 · 11 = 66 бит = 8,… → 9 байт
на 60 паролей:
I = 60 · 9 байтов = 540 байт
округление вверх

Конец фильма
ПОЛЯКОВ Константин Юрьевич
д.т.н., учитель информатики
ГБОУ СОШ № 163, г. Санкт-Петербург
[email protected]
ЕРЕМИН Евгений Александрович
к.ф.-м.н., доцент кафедры мультимедийной дидактики и ИТО ПГГПУ, г. Пермь
[email protected]