Динамическая память, динамические переменные в С++

Определение, создание и работа с динамическими переменными
int x = 15; - Описана статическая переменная x, в статической памяти ей выделено место – 4 байта и записано в них число 15
int *x - описан указатель x на переменную целого типа – статической переменной x в статической памяти выделено место, достаточное для хранения адреса байта памяти;
x = new(int) - в динамической памяти выделено место для хранения величины целого типа и адрес этой области памяти присвоен указателю x.
стат. память динам. память стат. память динам. память
x *x = 15; x *x 15
Здесь x – имя указателя, значением которого является адрес байта динамической памяти, начиная с которого размещается динамическая переменная - *x. Значением динамической переменной в результате выполнения оператора присваивания *x = 15; является число 15.

Определение, создание и работа с динамическими переменными
Оператор cout << x << ”\t” <<*x выведет на экран адрес области динамической памяти и содержимое этой области – значение динамической переменной.
Создать динамическую переменную можно двумя способами:
описать указатель
<тип> * <идентификатор>, например, int *x
обратиться к стандартной функции new, которая выделяет в динамической памяти область, достаточную для хранения величины, определяемой параметром этой функции, и присваивает указателю адрес этой области
<указатель> = new (<тип>), например, x = new(int)‏
2. одним оператором описать указатель и обратиться к функции new
<тип> * <идентификатор> = new(<тип>),
например, int *x = new (int);
Круглые скобки можно не писать, т.е. правильно и так:
int *x = new int;
Мы говорили, что любому указателю можно присвоить в качестве значения NULL

Определение, создание и работа с динамическими переменными
x = NULL – говорит о том, что указатель x ни на что не ссылается. Графически х
Указатели можно сравнивать на равенство и неравенство, они могут участвовать в операторах присваивания. После описания указателя, он может иметь произвольное, неопределенное значение. И если его использовать без предварительного присваивания x = NULL, или обращения к функции new, результат будет непредсказуемым.
Динамическую переменную можно использовать только после ее создания с помощью функции new. И для динамической переменной допустимы все операции типа, указанного в описании соответствующего указателя.
После использования динамической переменной ее необходимо удалить, освободить занимаемую ее динамическую память. Это можно сделать с помощью функции
delete <имя указателя>;
Функция delete не возвращает значение, обращение к ней - это самостоятельный оператор, в отличие от функции new.

работа с динамическими переменными
int *x = new int;
*x = 15;
…………..
delete x;
Если вместо delete x написать x = Null, то место в динамической памяти будет занято, но доступ к этой области памяти будет утерян, графически можно представить так:
x 15
примеры использования указателей и динамических переменных.
1) int *x = new (int), *y;
описаны два указателя x и y и создана динамическая переменная x
2) *x = 10; y = x;
динамической переменной x присвоили 10 и указателю y значение
указателя x, т.е. имеем два указателя на одну и туже область в ДП
3) *y = 7;
изменили содержимое этой области ДП с помощью указателя y
4) y = NULL; // указателю присвоили пустую ссылку
5) cout <<*x;
вывели содержимое области ДП с пом. указателя x, на экране будет число 7.
.

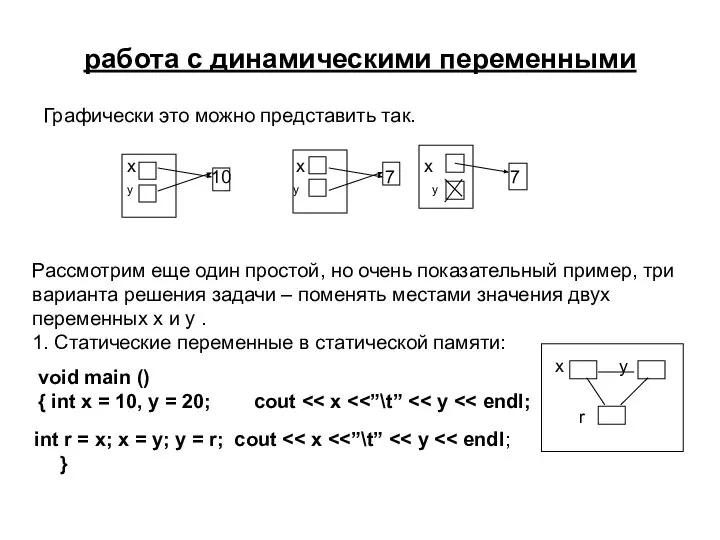
работа с динамическими переменными
Графически это можно представить так.
x x x
y y y
10 7 7
Рассмотрим еще один простой, но очень показательный пример, три варианта решения задачи – поменять местами значения двух переменных x и y .
1. Статические переменные в статической памяти:
void main ()
{ int x = 10, y = 20; cout << x <<”\t” << y << endl;
int r = x; x = y; y = r; cout << x <<”\t” << y << endl;
}
x y
r

работа с динамическими переменными
2. Меняем местами значения динамических переменных с помощью статической переменной r.
int main ()‏
{ int *x = new(int), *y = new (int), int r;
*x = 10; *y = 20; r
cout << *x <<”\t” << *y << endl;
r = *x; x y
*x = *y;
*y = r; *x *y
cout << *x <<”\t” << *y << endl;
-------------------------------------------
delete x; delete y; *
return 0;
}
r

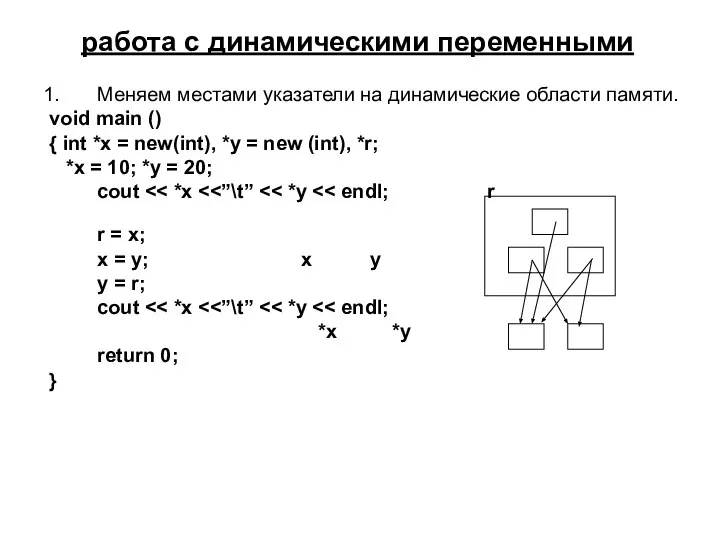
работа с динамическими переменными
Меняем местами указатели на динамические области памяти.
void main ()‏
{ int *x = new(int), *y = new (int), *r;
*x = 10; *y = 20;
cout << *x <<”\t” << *y << endl; r
r = x;
x = y; x y
y = r;
cout << *x <<”\t” << *y << endl;
*x *y
return 0;
}

Работа с динамическими переменными.
….Зачем нужны динамические переменные?....
Можно создать статический массив записей (структур), но работать с ним будет очень сложно, например, следить за размерностью при добавлении и удалении данных.
Но можно создать динамическую структуру данных – список, каждый элемент которого может быть описан так:
struct stud {
string fio;
int kurs;
……………
stud *next ;
};
Здесь в структуре типа stud введено поле, тип которого определяется указателем определяемого типа stud *next, т.е. значением этого поля может быть адрес следующего студента в списке и нет необходимости фиксировать количество элементов в списке. Список, его размер, может быть увеличен по мере необходимости в процессе выполнения программы.

Абстрактные структуры данных.
….в наборах данных, подлежащих компьютерной обработке, присутствуют важные структурные отношения между элементами данных….
Чтобы наиболее эффективно использовать ЭВМ для обработки информации, необходимо хорошо понимать структурные отношения, существующие между данными, наиболее эффективные способы представления этих структур средствами выбранного языка программирования и методы их обработки. Обычно и язык программирования выбирают, исходя из наличия в нем эффективных средств представления и обработки структур данных, возникающих при решении конкретной задачи на компьютере.
рассмотрим такие абстрактные структуры данных, как стек, очередь, дек, дерево, граф,….
Рассмотрим вначале понятия линейный список и связный список. Дональд Кнут так определяет линейный список (Л. Сп.) и возможные операции над линейными списками.
Л. Сп. – это множество, состоящее из n >=0 компонент, структурные свойства которого ограничиваются линейным, одномерным относительным положением компонент. x[1], x[2], …..x[n], причем, если n>0, то x[1] – первая компонента, а x[n] – последняя и для любого 1< i < n x[i-1] компонента предшествует x[i] – ой, а x[i+1] – ая следует за ней.

Абстрактные структуры данных.
С линейными списками могут быть выполнены следующие операции:
Получить доступ к к-й компоненте списка, чтобы посмотреть и/или изменить содержимое ее полей,
Включить новую компоненту в список перед к-ой компонентой,
Исключить из списка к-ую компоненту,
Объединить два или более списка в один,
Разбить Л. Сп на два или более Л. Сп.
Сделать копию Л. Сп.
Определить количество компонент в списке,
Выполнить сортировку компонент списка по значениям некоторых полей,
Найти в списке компоненту с заданным значением некоторого поля.

Линейный связный список (ЛССп) – это конечное множество компонент, каждая из которых состоит из двух частей: информационной (info) и указующей (link)…..
Наиболее часто используются однонаправленные и двунаправленные Л.С.Сп.
Если указующая часть содержит один адрес, указывает какая компонента следует за данной, то такой ЛССп называют однонаправленным, односвязным списком.
Если указующая часть содержит два адреса – это двунаправленный ЛССп. Возможно использование и многосвязных линейных списков. Графически однонаправленный и двунаправленный список можно представить так:
info link 0
Линейный связный список (ЛССп)

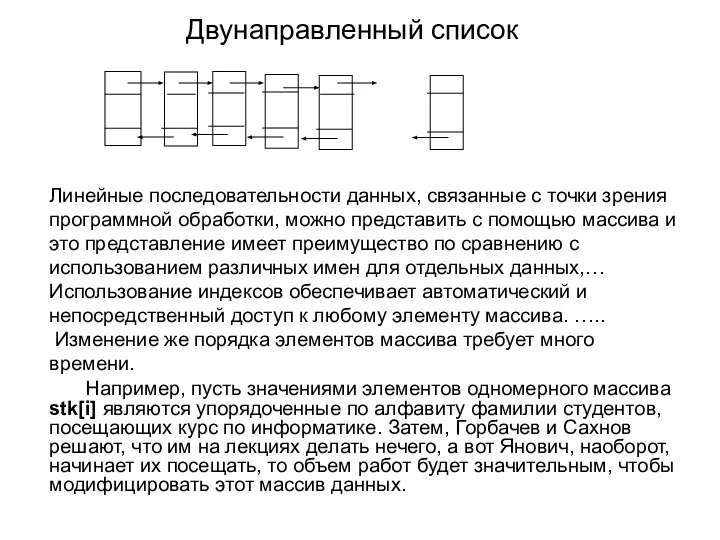
Двунаправленный список
Линейные последовательности данных, связанные с точки зрения программной обработки, можно представить с помощью массива и это представление имеет преимущество по сравнению с использованием различных имен для отдельных данных,…
Использование индексов обеспечивает автоматический и непосредственный доступ к любому элементу массива. …..
Изменение же порядка элементов массива требует много времени.
Например, пусть значениями элементов одномерного массива stk[i] являются упорядоченные по алфавиту фамилии студентов, посещающих курс по информатике. Затем, Горбачев и Сахнов решают, что им на лекциях делать нечего, а вот Янович, наоборот, начинает их посещать, то объем работ будет значительным, чтобы модифицировать этот массив данных.

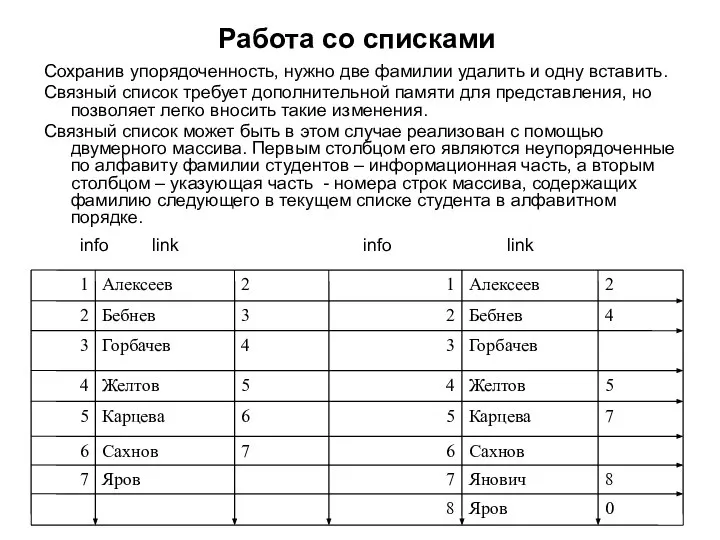
Работа со списками
Сохранив упорядоченность, нужно две фамилии удалить и одну вставить.
Связный список требует дополнительной памяти для представления, но позволяет легко вносить такие изменения.
Связный список может быть в этом случае реализован с помощью двумерного массива. Первым столбцом его являются неупорядоченные по алфавиту фамилии студентов – информационная часть, а вторым столбцом – указующая часть - номера строк массива, содержащих фамилию следующего в текущем списке студента в алфавитном порядке.
info link info link

Линейные связные списоки
Двумерный массив stk{i,j] размером 2*n может работать как Л.С.Сп. Список может быть реализован с помощью динамических переменных.
В общем случае трудно спроектировать единственный метод представления линейных списков, при котором все перечисленные Кнутом операции выполнялись бы эффективно. Кроме того при решении конкретных задач часто и нет необходимости в реализации всех операций. Поэтому существуют различные типы линейных списков в зависимости от главных операций, которые с ними выполняются. Наиболее часто применяемыми в программировании являются стеки, очереди, деки, деревья.
Стек – это линейный список, в котором все включения и исключения (ввод и вывод данных) и всякий доступ к данным осуществляется с одной стороны.
Очередь – это линейный список, в котором все включения (ввод, добавление компонент) производится с одной стороны, а все исключения (вывод) и всякий доступ производятся с другой стороны списка.
Дек – это очередь с двумя концами, т.е. это список, в котором все включения и все исключения и все операции могут выполняться на обоих концах списка.
Эти структуры можно представить графически.

Стек
Реализация стека. Стек – это настолько популярная структура данных, что во многих ЭВМ она реализуется аппаратно
Стек это линейный список, имеющий одну точку доступа и называется она вершиной стека, второй конец списка недоступен. Стек работает по принципу последний вошел – первый вышел и поэтому его называют структурой
LIFO (Last In – First Out). Описание стека помощью массива:
const int stacksize = 100;
int stack[stacksize], x, sp;
Компонентами стека могут быть величины различного типа, здесь int. Для работы со стеком нужно уметь обратиться к вершине стека, для этой цели вводится специальная переменная, называемая указателем стека, здесь sp (stack pointer). Чаще всего она указывает на первый свободный элемент стека, т.е. ее значением является номер элемента массива, не занятого информацией. Поэтому вначале работы, когда стек пуст, указатель стека sp указывает на первый элемент массива. Оператор присваивания
sp = 0; - инициализирует стек, делает его пустым.
Кроме инициализации над стеком производятся две операции:
Положить в стек и
Взять из стека.

Стек
На С++ эти операции реализуются так:
1. stack[sp] = x; // положить x на вершину стека,
sp = sp + 1; // указатель стека переместить на след-ую комп-ту
2. sp = sp - 1;
x = stack[sp];
т.к. sp указывает на первый свободный элемент стека, вначале указатель уменьшаем на единицу, а затем переменной x присваиваем значение последнего элемента в стеке.
…С учетом крайних ситуаций операции реализуются так:
Положить в стек:
if (sp = = stacksize) cout << “стек полон \n”;
else { stack[sp] = x; sp = sp + 1; };
Взять из стека:
if ( sp < 1) cout << “стек пуст \n”;
else {sp = sp - 1; x = stack[sp]; };
Указатель стека sp может указывать на первый занятый элемент в стеке, на его вершину, тогда операции положить в стек и взять из стека преобразуются так:
1. sp = sp + 1; stack[sp] = x;
2. x = stack[sp]; sp = sp – 1;

пример использования стека
Получение обратной польской записи выражения.
Существуют три формы записи выражений: 1) инфиксная, 2) префиксная и 3) постфиксная. Инфиксная запись – это привычная нам запись выражения, когда знаки операций стоят между операндами, например,
x + y * z – a/(b + c)‏
В префиксной записи знаки операций выносятся вперед
- + * x y z / + a b c
А в постфиксной форме знаки операций ставятся после операндов. Постфиксную запись называют обратной польской записью (ОПЗ). Во всех трансляторах для вычисления арифметических и логических выражений используется ОПЗ.
x y z * + a b c + / -
В ОПЗ отсутствуют скобки, а знаки операций выполняются в порядке их написания, таким образом выражение в виде ОПЗ может быть вычислено за один проход слева направо. Для преобразования инфиксной формы в постфиксную существуют различные алгоритмы, приведем алгоритм стека с приоритетами, предложенный голландским ученым Дейкстра. Пусть входная строка это выражение в обычной, инфиксной форме, а выходная строка – выражение в форме ОПЗ.

пример использования стека
Идея алгоритма : операнды из входной строки сразу попадают в выходную строку, а знаки операций прежде чем попасть в выходную строку должны побывать в стеке по следующему правилу:
всем знакам операций и скобкам присваивается приоритет знак приоритет
( 0
) 1
+ - 2
* / 3
Если очередной символ входной строки это знак операции и его
приоритет равен нулю или больше приоритета знака, находящегося на вершине стека, то этот знак из входной строки помещается в стек, в противном случае из стека в выходную строку выталкиваются все знаки с приоритетом большим или равным приоритету входного знака. После этого знак из входной строки помещается на вершину стека.
Особым образом обрабатываются скобки. Левая скобка обязательно попадает в стек, и т.к. ее приоритет = 0, ее не может вытолкнуть из стека ни один знак операции, это может сделать только правая скобка.

Если очередным символом во входной строке является правая скобка, то из стека выталкиваются в выходную строку все знаки операций до первой левой скобки, скобки же в выходную строку не помещаются, они взаимноуничтожаются. После просмотра всей входной строки, просматривается содержимое стека и из него в выходную строку выводятся все оставшиеся там знаки операций. Так получается ОПЗ арифметических и логических выражений в трансляторах. Последовательность выполнения алгоритма на примере:
x y z * + a b c + / - + x + y * z – a/(b + c)‏
(
/
-
*
+
После получения ОПЗ арифметическое выражение вычисляется слева направо так: если очередной символ строки – это операнд, то просмотр продолжается, если очередным символом является знак операции, то эта операция выполняется над двумя операндами, стоящими левее него. Результат записывается на место первого операнда. Графически это можно представить так:
x y z * + a b c + / -

Очередь.
Очередь. Очередь – это абстрактная структура данных, которая работает по принципу FIFO (First In First Out) первый пришел – первый ушел….
Доступ к данным в очереди возможен с двух концов, поэтому необходимы две переменные, определяющие адреса входа в очередь и выхода из нее. В литературе часто используются имена tail - хвост и head - голова, или front - начало и rear - конец соответственно для определения хвостовой и головной части. Очередь, как и стек, можно описать и реализовать с помощью массива. Очередь, рассчитанная на 100 элементов, может быть описана так:
const int n = 100;
float Queue[n], x;
int head, tail;
Элементами массива, компонентами очереди могут быть величины любого типа, здесь - float. Основные операции с очередью, как и со стеком:
инициализация очереди
добавить элемент в очередь (положить в очередь)‏
удалить элемент из очереди (взять из очереди).

Очередь.
Инициализация очереди заключается в присваивании начальных значений переменным head и tail. Если очередь пуста, положим head и tail равными единице:
head = 1; tail = 1;
head – указывает на первый элемент в очереди, а tail, также как и в стеке, может указывать на последний элемент в очереди или на первую свободную, доступную для ввода данных ячейку очереди. Представим графически несколько ситуаций работы с очередью.
tail
head
tail
head
tail
head
tail
head
head
tail
Вначале работы tail >= head. Чтобы не останавливать работу и не допустить переполнения массива, мы можем присвоить переменной tail значение 1 и продолжить заполнять очередь с начала массива. Таким образом получается закольцованная структура очереди.

Очередь.
Чтобы отличить пустую очередь от полностью заполненной в очереди, смоделированной с помощью закольцованного массива, приходится оставлять одну ячейку свободной, и условием того, что очередь пустая, используют выражение
head = tail, а условием того, что очередь заполнена, head = tail +1. Хвост не может подойти вплотную к голове, между ними пустая ячейка.
2. Взять элемент из очереди:
if (head = tail) then
вывод “очередь пуста”;
else { x := Queue[head];
head := head +1;
if ( head = n ) head :=1;
};
3. Добавить элемент в очередь:
r := tail +1;
if (r = n) r := 1;
if (r = head) then вывод “очередь полна”;
else { Queue[tail] := x;
tail := r;
}

Очередь.
Здесь head указывает на первый элемент в очереди, а tail на ячейку, следующую за последним элементом в очереди.
Еще один вариант реализации очереди с помощью массива, состоящего из n+1 элемента, описанного от 0 до n, когда tail указывает на последний элемент в очереди, а head - на ячейку, предшествующую первому элементу в очереди. А проверка состояния очереди, пустая она или заполненная, отличается тем, что при добавлении элемента в очередь вначале индекс tail увеличивается на единицу, а затем осуществляется сравнение if tail = = head, а при взятии элемента из очереди вначале проверяется совпадает ли голова с хвостом, а затем увеличивается индекс на единицу.
инициализация очереди
head = 0; tail = 0;
взять элемент из очереди:
if (head = = tail)
cout << “очередь пуста” << endl;
else { head = ((head +1)% n) ;
x = Queue[head];
};

Очередь.
добавить элемент в очередь:
tail = ((tail+1)% n);
if (tail = =head) cout <<”очередь полна” <
else Queue[tail] = x;
Изменение индекса массива head ( tail), движение по кольцу осуществляется за счет операции %. Если значение tail < n – 1, то tail увеличивается на единицу
(1 % 100) = 1, (2 % 100) = 2 и т.д.,
но как только tail станет равным n – 1, то tail присваивается ноль.
((99 + 1) % 100) = 0.

Деревья.
Создание теории деревьев связывают с именами инженера – электрика Г. Кирхгофа и математика А. Кэли, которые в середине 19-го века впервые разработали и применили ее для исследования электрических цепей и описания строения углеводорода соответственно….
Существуют различные определения дерева, например, Никлаус Вирт в книге «Алгоритмы + структуры данных = программы» приводит следующее определение:
Опр.1. Древовидная структура с базовым типом Т – это либо: 1) пустая структура; либо 2) узел типа Т, с которым связано конечное число древовидных структур с базовым типом Т, называемых поддеревьями. Используя такое определение, можно сказать, что линейный список – это вырожденное дерево, т.е. это древовидная структура, у которой каждый узел имеет не более одного поддерева.
Существуют различные способы графического представления древовидных структур. Представим одно и тоже дерево различными способами, если базовым типом является множество букв.

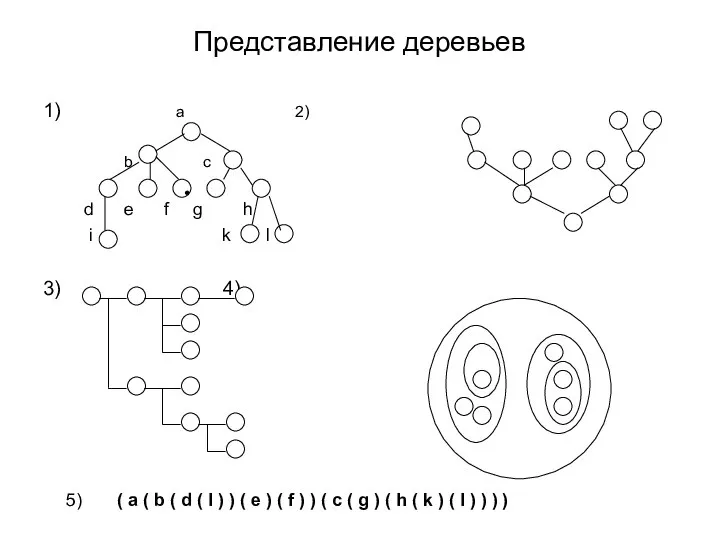
Представление деревьев
1) a 2)‏
b c
d e f g h
i k l
3) 4)‏
5) ( a ( b ( d ( I ) ) ( e ) ( f ) ) ( c ( g ) ( h ( k ) ( l ) ) ) )

Опр.2. Дерево – это неориентированный связный граф без циклов.
Опр. 3. Дерево – это неориентированный, связный граф с n вершинами n -1 ребром.
Опр. 4. Дерево – это конечное множество элементов, называемых узлами, таких что:
между узлами существует связь, отношение типа «исходный - порожденный». Узел y, который находится непосредственно под узлом x, называется непосредственным потомком (сыном) x, а узел x называется предком (отцом) y – ка. Если x находится на уровне i , то y на уровне i+1.
лишь один узел не имеет исходного (отца), он называется корнем дерева. Максимальный уровень элемента дерева называется высотой или глубиной дерева.
остальные узлы имеют только одного отца и могут иметь ноль или более потомков. Если узел не имеет сыновей, он называется терминальным, узлом или листом дерева, узел, не являющийся терминальным, называется внутренним. Количество непосредственных потомков узла называется его степенью. Количество ветвей или ребер, которые необходимо пройти, чтобы продвинуться от корня к узлу x , называется длиной пути к x . отношение исходный – порожденный действует только в одном направлении, т.е. для любого узла его потомки никогда не станут его предками.

Исходя из этого определения, можно сказать, что рисунки 1, 2 и 3 учитывают связи между узлами и положение корня. 4 –ый способ определяет дерево как вложенные множества, 5 –ый – как вложенные скобки.
Упорядоченным деревом называется дерево, у которого ветви каждого узла (узлы) упорядочены, т.е. следующие два дерева будут различны:
1 1
2 3 3 2
….
Бинарное дерево – это множество узлов, каждый из которых либо пуст, либо состоит из узла, связанного с двумя различными бинарными деревьями, называемыми левым и правым поддеревом узла, т.е. каждый узел бинарного дерева имеет 0, 1 или 2 сына.
Упорядоченность бинарных деревьев…

Операции над деревьями, представление массивом
Важнейшими операциями над деревьями являются:
Построение дерева ….
Добавление элемента в упорядоченное дерево….
Удаление элемента из упорядоченного дерева…
Обход бинарного дерева…1) + a b 2) a + b 3) a b +
1 2 3
2 3 1 3 1 2
Поиск в дереве величины с ключом, равным данному
Представление в компьютере дерева с помощью массива.
Компоненты массива, моделирующего двоичное дерево, должны быть комбинированного типа, причем два поля должны указывать на левое и правое поддерево этого узла (содержать их адреса), а остальные поля - это информационная часть - данные, хранящиеся в этом узле. Представим в виде дерева, а дерево в виде массива арифметическое выражение:
(a + b / c ) * ( d – e * f )

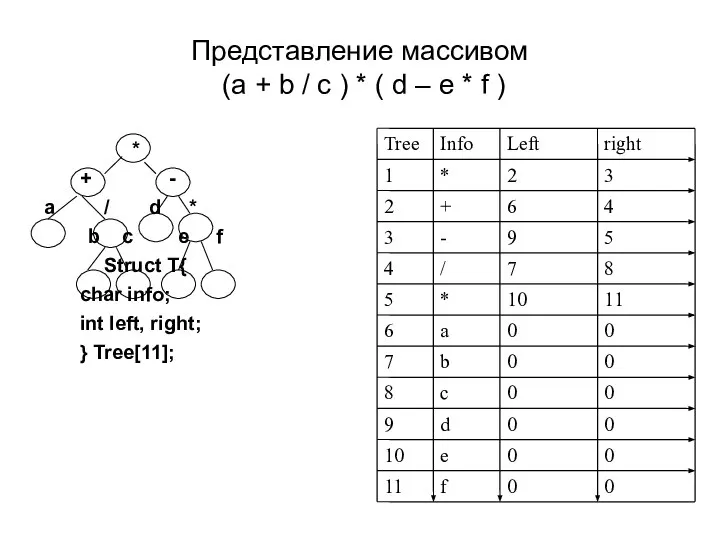
Представление массивом
(a + b / c ) * ( d – e * f )
*
+ -
a / d *
b c e f
Struct T{
char info;
int left, right;
} Tree[11];

Представление дерева массивом
Представление дерева массивом позволяет легко находить путь от корня к заданному узлу, если значением каждого элемент A[ i ] является указатель на родителя узла i. Корень ссылается либо на себя, либо на 0. Элементы массива могут быть, как и в предыдущем случае, комбинированного типа, но значением одного из полей является указатель на непосредственного родителя, например, дерево вида:
1
3
4 5 9 10
6 7 8
М. пред-ть массивом: a[1] a[2] a[3] a[4] a[5] a[6] a[7] a[8] a[9] a10]
Значения массива: 0 1 1 2 2 5 5 5 3 3
цикл while (b) {cout << b <<“\t”; b = a[b] };
для b= 7 выведет на экран путь от вершины b к корню: 7 5 2 1

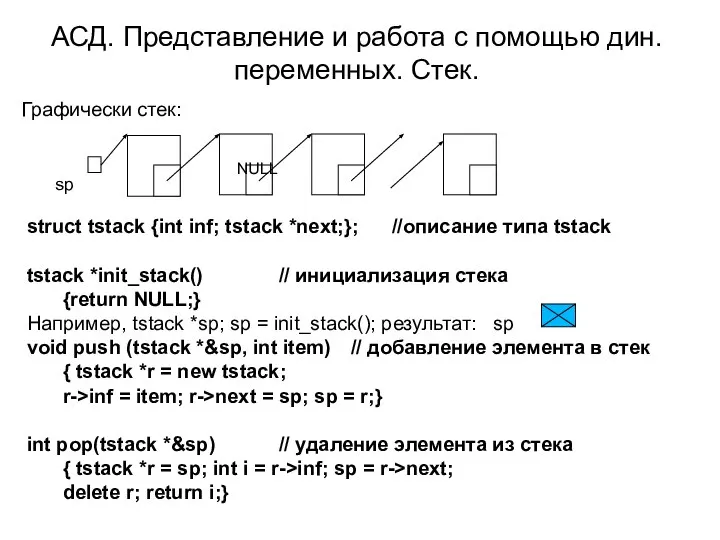
АСД. Представление и работа с помощью дин. переменных. Стек.
Графически стек:
NULL
sp
struct tstack {int inf; tstack *next;}; //описание типа tstack
tstack *init_stack() // инициализация стека
{return NULL;}
Например, tstack *sp; sp = init_stack(); результат: sp
void push (tstack *&sp, int item) // добавление элемента в стек
{ tstack *r = new tstack;
r->inf = item; r->next = sp; sp = r;}
int pop(tstack *&sp) // удаление элемента из стека
{ tstack *r = sp; int i = r->inf; sp = r->next;
delete r; return i;}

Стек с помощью дин. переменных
просмотр элемента, расположенного на вершине стека
int peek(tstack *sp)
{return sp->inf;};
определение стека на пустоту
int empty_stack(tstack *sp)
{return(sp) ? 0:1;}; //0, если стек не пуст и 1, если пуст
Объединив все функции в файл с именем stackint.h и сохранив его а папке INCLUDE, можно подключать его к любой программе с помощью директивы
#include
Пример: переписать содержимое файла h в файл g в обратной последовательности с помощью стека.

#include
#include "stackint.h"
#include
using namespace std;
void main() {
FILE *h = fopen("input_stack.txt”,"r"); // файл h для чтения
FILE *g = fopen("output.txt","w"); // файл g для записи
int i; tstack *sp = init_stack(); // инициализация sp = NULL
while (!feof(h))
{fscanf(h, "%d", &i);
push(sp, i); printf("%d\t", i);
};
cout << "\n";
while (!empty_stack(sp)) // пока стек не пуст
{ i = pop(sp);
printf("%d\t",i); fprintf(g,"%d\t",i);
};
fcloseall();
}

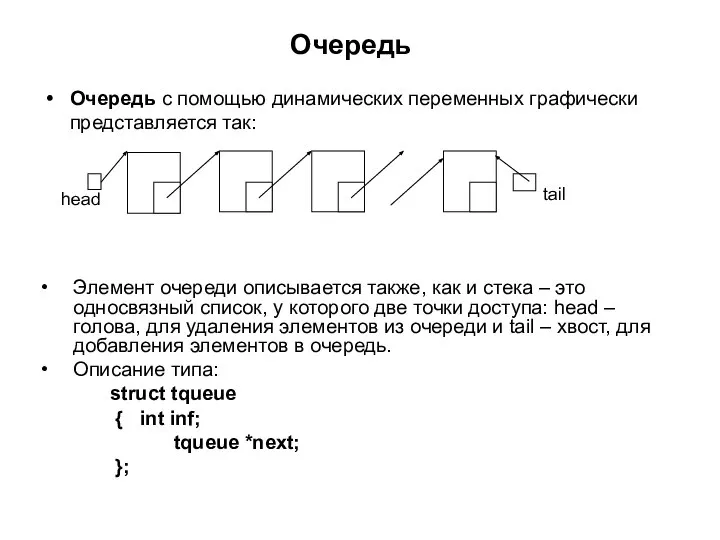
Очередь
Очередь с помощью динамических переменных графически представляется так:
tail
head
Элемент очереди описывается также, как и стека – это односвязный список, у которого две точки доступа: head – голова, для удаления элементов из очереди и tail – хвост, для добавления элементов в очередь.
Описание типа:
struct tqueue
{ int inf;
tqueue *next;
};

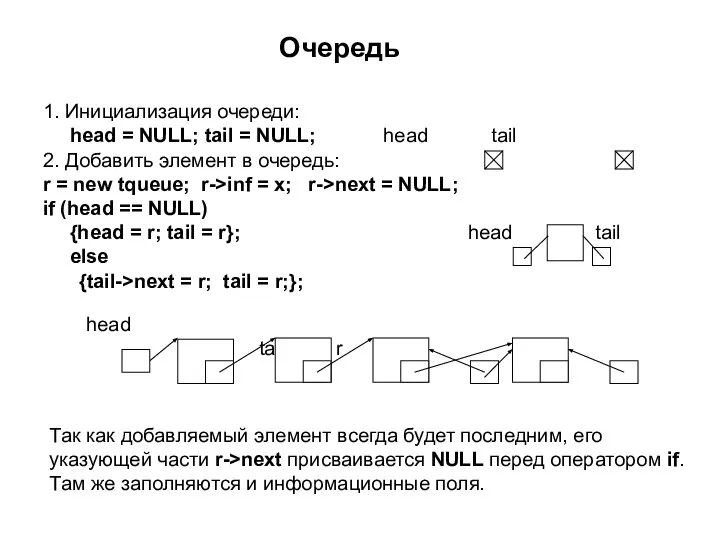
Очередь
1. Инициализация очереди:
head = NULL; tail = NULL; head tail
2. Добавить элемент в очередь:
r = new tqueue; r->inf = x; r->next = NULL;
if (head == NULL)‏
{head = r; tail = r}; head tail
else
{tail->next = r; tail = r;};
head
tail r
Так как добавляемый элемент всегда будет последним, его указующей части r->next присваивается NULL перед оператором if. Там же заполняются и информационные поля.

3. Взять элемент из очереди:
if (head != NULL)‏
{r = head; x = head->inf; head = head->next;
delete r;}
r tail
head
Освободить динамическую память, занятую очередью:
void clear_queue(tqueue *&head)‏
{ tqueue *r;
while (head != NULL)‏
{ r = head; head = head->next; delete r};
}
Для решения задач с использованием очереди, удобнее также, как и для стека, создать подключаемый файл с набором функций, реализующих основные операции, сохранить его в библиотеке подключаемых файлов и затем подключать его к своей программе с помощью директивы include.

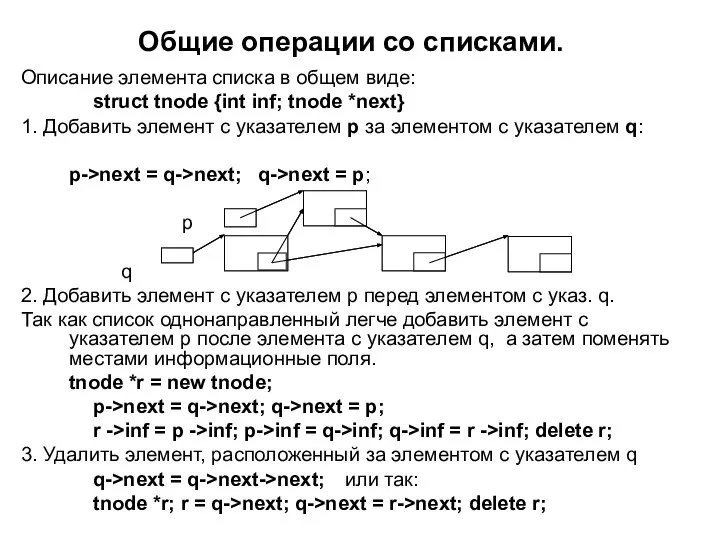
Общие операции со списками.
Описание элемента списка в общем виде:
struct tnode {int inf; tnode *next}
1. Добавить элемент с указателем p за элементом с указателем q:
p->next = q->next; q->next = p;
p
q
2. Добавить элемент с указателем p перед элементом с указ. q.
Так как список однонаправленный легче добавить элемент с указателем p после элемента с указателем q, а затем поменять местами информационные поля.
tnode *r = new tnode;
p->next = q->next; q->next = p;
r ->inf = p ->inf; p->inf = q->inf; q->inf = r ->inf; delete r;
3. Удалить элемент, расположенный за элементом с указателем q
q->next = q->next->next; или так:
tnode *r; r = q->next; q->next = r->next; delete r;

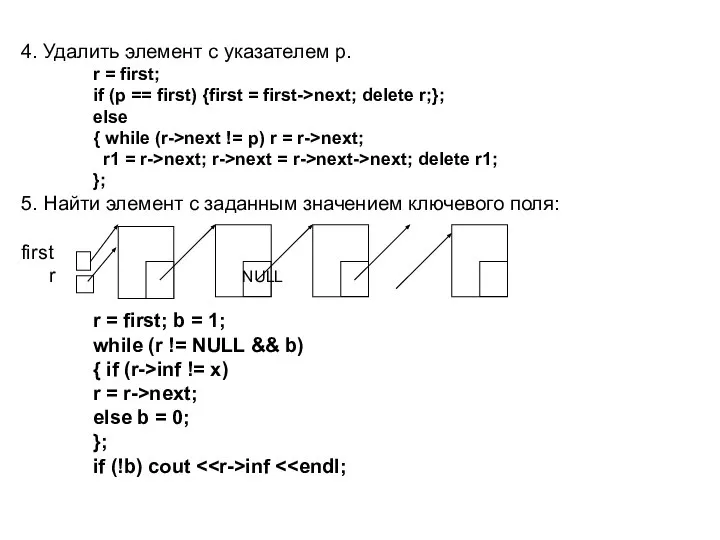
4. Удалить элемент с указателем p.
r = first;
if (p == first) {first = first->next; delete r;};
else
{ while (r->next != p) r = r->next;
r1 = r->next; r->next = r->next->next; delete r1;
};
5. Найти элемент с заданным значением ключевого поля:
first
r NULL
r = first; b = 1;
while (r != NULL && b)‏
{ if (r->inf != x)‏
r = r->next;
else b = 0;
};
if (!b) cout <
inf <

Бинарные деревья, программирование их с помощью динамических переменных.
Дерево – это структура данных, которая может быть
рекурсивно определена и поэтому для работы с деревьями
предпочтительными оказываются рекурсивные алгоритмы.
struct tnode
{ int inf;
………………………
tnode *left,*right;
};
tnode *p,*q,*r;
Представили дерево для выражения (a + b / c) * (d – e * f), здесь
информационное поле символьного типа.
Реализуем основные операции:
построение дерева 2. обход дерева 3. добавление узла в
дерево 4. поиск узла с заданным значением ключевого поля
5. удаление узла из дерева.

Построение дерева с n узлами и минимальной высотой
Идеально сбалансированное дерево…
Пусть информационной частью будут номера вершин, вводимых с клавиатуры. Рекурсивный алгоритм:1) взять один узел в качестве корня; 2) построить левое поддерево, состоящее из
nl = n / 2 узлов тем же способом; 3) построить правое поддерево, состоящее из nr = n – nl – 1 УЗЛОВ тем же способом.
Функция, не возвращающая значение:
void Tree (tnode *&t, int n)‏
{tnode *r, int nr, nl, x;
if (n == 0) t = NULL;
else { nl = n / 2; nr = n – nl – 1;
cout <<’введите номер вершины’ << endl;
cin >> x;
r = new tnode; r->inf = x;
Tree(r->left, nl); Tree(r->right, nr);
};
};

Идеально сбалансированное дерево.
Функция, возвращающая значение:
tnode *Tree (int n)
{ tnode *r; int nr, nl, x;
if (n == 0) return NULL;
else {nl = n / 2; nr = n- nl - 1; cout <
cout <<“введите номер вершины" <<"\t";
cin >> x;
r = new tnode; r->inf = x;
r->left = Tree(nl); r->right = Tree(nr);
return r;
};
};

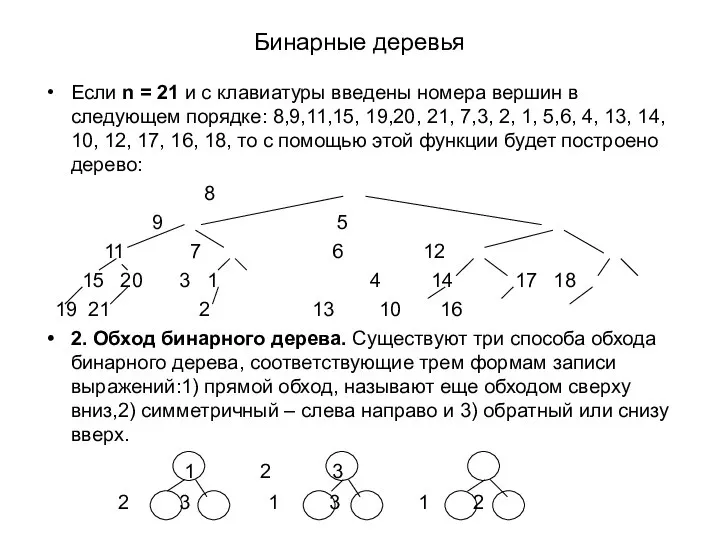
Бинарные деревья
Если n = 21 и с клавиатуры введены номера вершин в следующем порядке: 8,9,11,15, 19,20, 21, 7,3, 2, 1, 5,6, 4, 13, 14, 10, 12, 17, 16, 18, то с помощью этой функции будет построено дерево:
8
9 5
11 7 6 12
15 20 3 1 4 14 17 18
19 21 2 13 10 16
2. Обход бинарного дерева. Существуют три способа обхода бинарного дерева, соответствующие трем формам записи выражений:1) прямой обход, называют еще обходом сверху вниз,2) симметричный – слева направо и 3) обратный или снизу вверх.
1 2 3
2 3 1 3 1 2

Обходы бинарного дерева:
void Preorder (tnode *&t) //прямой
{ if (t != NULL)‏ { cout << t->inf <<’\t’;
Preorder (t->left);
Preorder (t->right);
};
};
void Inorder (tnode *&t) // симметричный
{ if (t != NULL)‏
{ Inorder (t->left);
cout << t->inf <<’\t’;
Inorder (t->right);
};
};
void Postorder (tnode *&t) // обратный
{ if (t != NULL)‏
{ Postorder (t->left); Postorder (t->right); cout << t->inf <<’\t’; };
};

#include “iostream” // построение и обход дерева мин. высоты
using namespace std;
struct tnode {int inf; tnode *left,*right;};
void Tree (tnode *&t, int n)
{ int nr, nl, x;
if (n==0) t = NULL;
else { nl=n / 2; nr=n-nl-1;
cout << “vvedite nomer vershini" << "\t"; cin >> x;
t = new tnode; t->inf= x; Tree(t->left, nl); Tree(t->right, nr);
};
};
void inorder(tnode *&t)
{ if (t!= NULL)
{ inorder(t->left); cout << t->inf << "\t"; inorder(t->right); };
};
int main ()
{ tnode *r; int n; cout << “vvedite kolichestvo vershin \t”; cin >>n;
Tree(r,n); inorder (r);
return 0;
};

Построение бинарного упорядоченного дерева
Пусть ключевое поле – это поле inf и мы рассматриваем
упорядоченное бинарное дерево, называемое деревом поиска.
Рекурсивная функция, которая осуществляет поиск заданного элемента в дереве и если его не находит, то включает его, добавляя его в качестве очередного листа:
void Search (int x, tnode *&t)‏
{ if(!t) //такого элемента нет, включаем его
{ t = new tnode; t->inf = x;
t-> left = NULL; t->right = NULL;
};
else if (x < t->inf) Search (x, t->left);
else if (x > t-> inf) Search (x, t->right);
else { cout<< t-> inf; //обработка найденного узла }
};
Эту функцию можно использовать для построения бинарного
упорядоченного дерева, вводя номера вершин, например, с клавиатуры или из файла

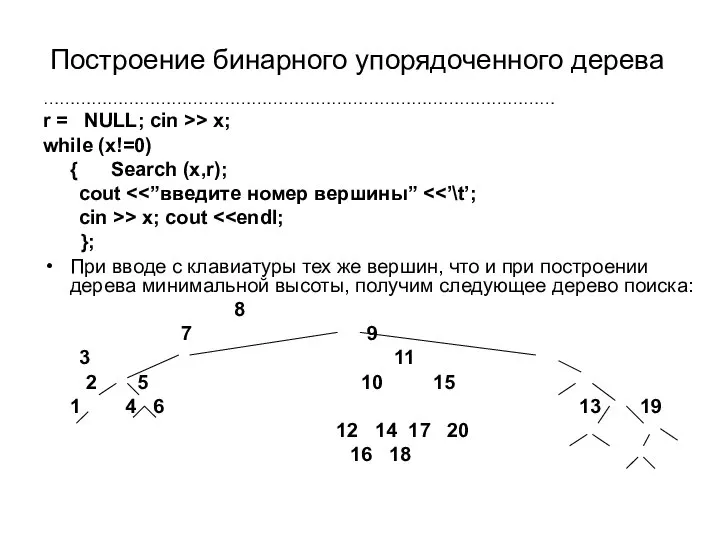
Построениe бинарного упорядоченного дерева
……………………………………………………………………………………
r = NULL; cin >> x;
while (x!=0)‏
{ Search (x,r);
cout <<”введите номер вершины” <<’\t’;
cin >> x; cout <
};
При вводе с клавиатуры тех же вершин, что и при построении дерева минимальной высоты, получим следующее дерево поиска:
8
7 9
3 11
2 5 10 15
1 4 6 13 19
12 14 17 20
16 18

Удаление из упорядоченного дерева
tnode *q;
void Del_node(int x, tnode *&t)‏
{ if (t == NULL)‏
{cout << “такого узла в дереве нет” << endl; };
else if (x < t->inf) Del_node (x, t->left)‏;
else if (x > t->inf) Del_node (x, t->right)‏;
else { //нашли удаляемый
q = t;
if (q->left == NULL) t = q->right;
else if (q->right == NULL) t = q->left;
else Del_vs (q->left);
delete q;
};
};
void Del_vs (tnode *&r)‏
{ if (r->right != NULL) Del_vs (r->right)‏;
else { q->inf = r->inf;
q = r; r = r->left;
};
};

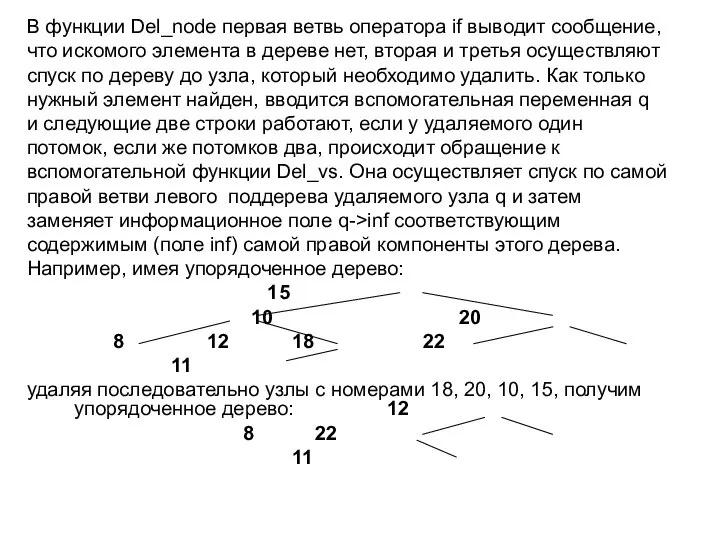
В функции Del_node первая ветвь оператора if выводит сообщение,
что искомого элемента в дереве нет, вторая и третья осуществляют
спуск по дереву до узла, который необходимо удалить. Как только
нужный элемент найден, вводится вспомогательная переменная q
и следующие две строки работают, если у удаляемого один
потомок, если же потомков два, происходит обращение к
вспомогательной функции Del_vs. Она осуществляет спуск по самой
правой ветви левого поддерева удаляемого узла q и затем
заменяет информационное поле q->inf соответствующим
содержимым (поле inf) самой правой компоненты этого дерева.
Например, имея упорядоченное дерево:
15
10 20
8 12 18 22
11
удаляя последовательно узлы с номерами 18, 20, 10, 15, получим упорядоченное дерево: 12
8 22
11

Создание, обход и удаление из дерева поиска
#include "iostream"
using namespace std;
struct tnode {int inf; tnode *left,*right;};
void Add_Tree (int x, tnode *&t) //добавление в дерево поиска
{ if(t)
if (x < t->inf) Add_Tree (x, t->left);
else Add_Tree (x, t->right);
else {t = new tnode; t->inf = x;
t-> left = NULL; t->right =NULL;
};
};
void inorder(tnode *&t) // симметричный обход
{ if (t!= NULL)
{ inorder(t->left);
cout << t->inf << "\t";
inorder(t->right);
};
};

tnode *q;
void Del_vs (tnode *&r); // прототип функции
void Del_node(int x, tnode *&t) //удаление из дерева поиска
{ if (t==NULL) cout << " такого узла в дереве нет" << endl;
else if (x < t->inf) Del_node(x, t->left);
else if (x>t->inf) Del_node(x, t->right);
else { //нашли удаляемый
q = t;
if (q->left == NULL) t = q->right;
else if (q->right == NULL) t = q->left;
else Del_vs (q->left);
delete q;
};
};
void Del_vs (tnode *&r)
{ if (r->right != NULL)
Del_vs (r->right);
else { q->inf = r->inf; q = r; r = r->left; };
};

int main ()
{ tnode *r; int x, n ;
r = NULL;
cout <<“введите номер вершины \t"; cin>>x;
while (x!=0)
{ Add_Tree (x,r);
cout <<“введите номер вершины" <<'\t';
cin >> x; cout << endl;
};
inorder (r);
cout <<“введите номер удаляемой вершины \t"; cin>>n;
Del_node(n,r); cout<<"\n";
inorder(r);
return 0;
}

Сильно ветвящиеся деревья
Сильно ветвящиеся деревья - это деревья у узлов которых может быть больше двух потомков. Узел такого дерева может быть представлен с помощью величины следующего типа:
const int n = ;
struct tnode
{ int inf1;
char inf2;
………………………
tnode *a[n];
};
Каждый узел содержит массив указателей на своих непосредственных потомков. Размерность массива n определяется максимально возможным количеством потомков у узлов данного дерева.

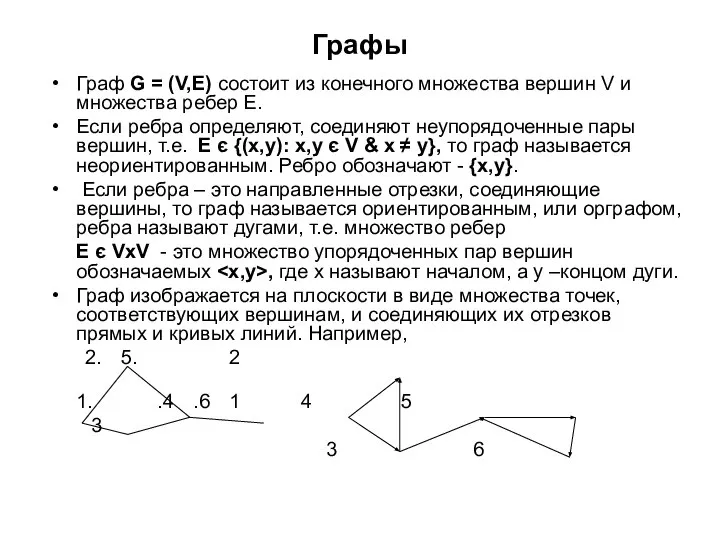
Графы
Граф G = (V,E) состоит из конечного множества вершин V и множества ребер E.
Если ребра определяют, соединяют неупорядоченные пары вершин, т.е. E є {(x,y): x,y є V & x ≠ y}, то граф называется неориентированным. Ребро обозначают - {x,y}.
Если ребра – это направленные отрезки, соединяющие вершины, то граф называется ориентированным, или орграфом, ребра называют дугами, т.е. множество ребер
E є VxV - это множество упорядоченных пар вершин обозначаемых
, где x называют началом, а y –концом дуги.
Граф изображается на плоскости в виде множества точек, соответствующих вершинам, и соединяющих их отрезков прямых и кривых линий. Например,
2. 5. 2
1. .4 .6 1 4 5
3
3 6

Графы
Если в графе G(V,E) ребро {u,v} или дуга
є E, то вершины u и v называются смежными, а ребро (дуга) - (u,v) называется инцидентным вершинам u и v.
Степень вершины…. полустепень захода…, полустепень исхода…,
Вершину нулевой степени называют изолированной.
Путем в графе ориентированном или неориентированном называют последовательность ребер вида (v1,v2) (v2,v3) (v3,v4)...(vk-1,vk) или последовательность вершин v1,v2,v3....vk, таких что v1 – начало, vk – конец, к – длина пути.
Длиной пути называется сумма длин входящих в него дуг, если длины дуг не заданы, то длина пути определяется как количество входящих в него дуг.
Путь называется простым, если все вершины кроме может быть первой и последней различны.
Путь называется замкнутым, если v1 = vk. Замкнутый путь, у которого все ребра различны называются циклом.
Растояние между двумя вершинами – это длина кратчайшего пути, соединяющего их.
Граф газывается связным, если для любой пары вершин существует соединяющий их путь.

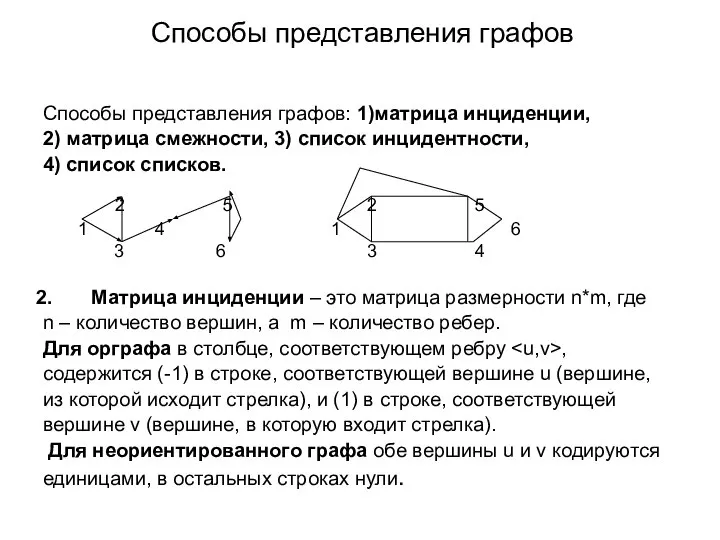
Cпособы представления графов
Cпособы представления графов: 1)матрица инциденции,
2) матрица смежности, 3) список инцидентности,
4) список списков.
2 5 2 5
1 4 1 6
6 3 4
Матрица инциденции – это матрица размерности n*m, где
n – количество вершин, а m – количество ребер.
Для орграфа в столбце, соответствующем ребру
,
содержится (-1) в строке, соответствующей вершине u (вершине,
из которой исходит стрелка), и (1) в строке, соответствующей
вершине v (вершине, в которую входит стрелка).
Для неориентированного графа обе вершины u и v кодируются
единицами, в остальных cтроках нули.

Cпособы представления графов
Для представленного орграфа матрица инциденции:
<1,2> <1,3> <3,2> <3,4> <5,4> <5,6><6,5>
1 -1 -1 0 0 0 0 0
2 1 0 1 0 0 0 0
3 0 1 -1 -1 0 0 0
4 0 0 0 1 1 0 0
5 0 0 0 0 -1 -1 1
6 0 0 0 0 0 1 -1
Для представленного неориентированного графа матрица инциденции:
(1,2) (1,3) (1,5) (2,3) (2,5) (3,4) (4,5)(4,6) (5,6)‏
1 1 1 1 0 0 0 0 0 0
2 1 0 0 1 1 0 0 0 0
3 0 1 0 1 0 1 0 0 0
4 0 0 0 0 0 1 1 1 0
5 0 0 1 0 1 0 1 0 1
6 0 0 0 0 0 0 0 1 1

Cпособы представления графов
На практике ребер в графе бывает обычно больше, чем вершин...
Второй способ представления графов с помощью матрицы
смежности оказывается более рациональным. Это матрица,
размерности n*n, где n – количество вершин, причем ее элементы
a i,j =1 если ребро (i,j) существует и a i,j = 0, если такого ребра нет.
Для неориентированного графа ребро {u,v} идет как от u к v, так и
от v к u, поэтому матрица смежности для такого графа всегда
симметрична относительно главной диагонали. Для
рассматриваемых графов матрицы смежности будут такими:
1 2 3 4 5 6 1 2 3 4 5 6
1 0 1 1 0 0 0 1 0 1 1 0 1 0
2 0 0 0 0 0 0 2 1 0 1 0 1 0
3 0 1 0 1 0 0 3 1 1 0 1 0 0
4 0 0 0 0 0 0 4 0 0 1 0 1 1
5 0 0 0 1 0 1 5 1 1 0 1 0 1
6 0 0 0 0 1 0 6 0 0 0 1 1 0

Cпособы представления графов
Для орграфа 2-я и 4-я строки нулевые, т.к. 2-я и 4-я вершины не
имеют исходящих дуг (такие вершины называются стоками
для орграфа)…. Третий способ еще более удобен – это
структура данных, называемая списком инцидентности, или
списком смежности. Эта структура содержит для каждой
вершины v є V, список всех вершин, смежных, прямо
достижимых из этой вершины, т.е. таких что есть ребро (u,v).
Для n вершинного графа список инцидентности
состоит из n линейных связных списков, начало каждого
списка хранится в специальном массиве. Так что элемент
массива Nach[i] хранит указатель на начало связного списка,
содержащего смежные с i-ой вершины. Графически списки
инцидентности для рассматриваемых графов могут быть
представлены так:
Nach[1] -> 2 --> 3 NULL Nach[1] -->2 --> 3 ---> 5 NULL
Nach[2] = NULL Nach[2]--> 1 --> 3 --> 5 NULL
Nach[3] -> 2 -->4 NULL Nach[3]--> 1 --> 2 --> 4 NULL

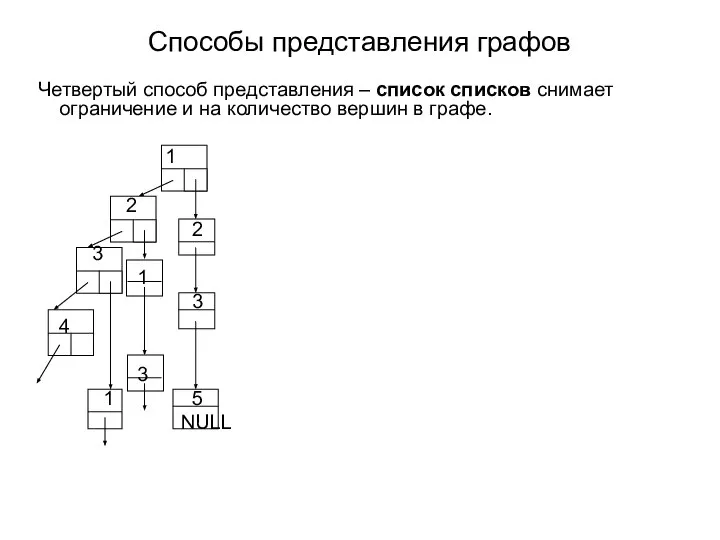
Cпособы представления графов
Четвертый способ представления – список списков снимает ограничение и на количество вершин в графе.
1
2
2
3
1
3
4
3
1 5
NULL

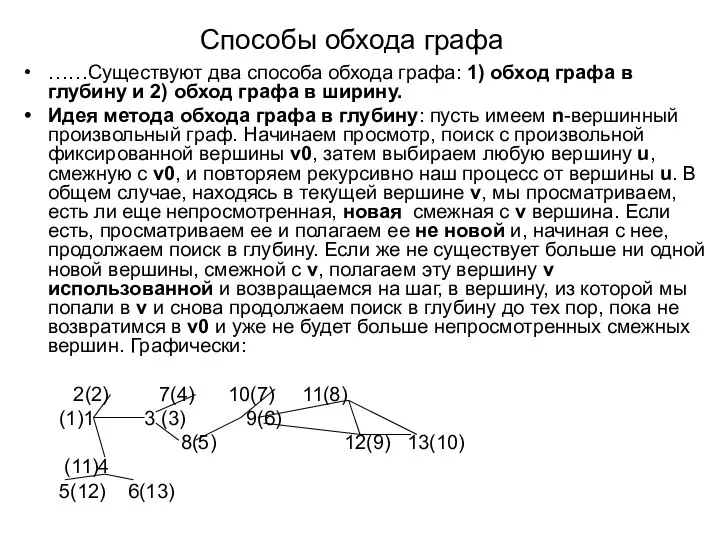
Способы обхода графа
……Существуют два способа обхода графа: 1) обход графа в глубину и 2) обход графа в ширину.
Идея метода обхода графа в глубину: пусть имеем n-вершинный произвольный граф. Начинаем просмотр, поиск с произвольной фиксированной вершины v0, затем выбираем любую вершину u, смежную с v0, и повторяем рекурсивно наш процесс от вершины u. В общем случае, находясь в текущей вершине v, мы просматриваем, есть ли еще непросмотренная, новая смежная с v вершина. Если есть, просматриваем ее и полагаем ее не новой и, начиная с нее, продолжаем поиск в глубину. Если же не существует больше ни одной новой вершины, смежной с v, полагаем эту вершину v использованной и возвращаемся на шаг, в вершину, из которой мы попали в v и снова продолжаем поиск в глубину до тех пор, пока не возвратимся в v0 и уже не будет больше непросмотренных смежных вершин. Графически:
2(2) 7(4) 10(7) 11(8)‏
(1)1 3 (3) 9(6)
8(5) 12(9) 13(10)‏
(11)4
5(12) 6(13)‏

Обход графа в глубину
Существуют рекурсивный и не рекурсивный алгоритмы, реализующие этот метод. Чтобы отличить просмотренную вершину от не просмотренной, вводится вспомогательный массив размерности n, и элемент его Nov[v] = false, если вершина уже просмотрена и true в противном случае. Запишем рекурсивный алгоритм на псевдокоде: DFS – Depth First Search:
Function DFS (v)
//величины Nov и Spisok - глобальные
begin
Просмотреть v; Nov[v] = false;
for (u є Spisok[v]) do
if (Nov[u]) DFS(u);
end;
Поиск в глубину в произвольном, не обязательно связном графе, может быть осуществлен обращением к этой функции так:
begin
for (v є V) do Nov[v] = true; // инициализация массива
for (v є V) do
if (Nov[v]) DFS(v);
end;

Обход графа в глубину
Здесь V – множество всех вершин данного графа
Spisok[v] – содержит номера вершин, смежных с v
Просмотреть вершину – это значит выполнить некоторые операции над данными, хранящимися в информационной части.
Посещается каждая вершина только один раз, т.к. просмотреть можно только ту вершину, у которой
Nov[v] = true,
сразу после просмотра этому элементу массива присваивается значение false
При решении задач на графы преимущества имеет иногда рекурсивный, иногда не рекурсивный алгоритм обхода графа в глубину. Рекурсия заменяется стеком, в который помещается вершина как только она просмотрена и удаляется из стека после того, как она использована, т.е. просмотрены все смежные с ней вершины.

Обход графа в глубину - не рекурсивный
function DFS1 (v);
begin stack = 0; v -> stack; просмотреть v; Nov[v] = false;
while (stack <> 0) do
begin t = stack[sp]; b = true;
while (spisok[t]<>0 and b) do
// поиск 1-й новой вершины в spisok[t]
begin u=spisok[t];
if (Nov(u))
then b = false // найдена новая вершина
else u= spisok[t];
end;
if (not b)‏
then //добавляем новую вершину в стек
begin u -> stack; просмотреть u; Nov[u] = false; end;
else //вершина t использована
stack -> t //удалить из стека верхний элемент
end;
end;

Нерекурсивный обход графа в глубину
function DFS1 (v);
begin
stack = 0; v -> stack; просмотреть v; Nov[v] = false;
while (stack <> 0) do
begin t = stack[sp]; b = true;
while (Nach[t]<>Null and b) do
// поиск 1-й новой вершины в spiske(t)
if (Nov[Nach[t]->k])
then b = false // найдена новая вершина
else Nach[t]=Nach[t]->next
if (not b)‏
then //добавляем новую вершину в стек
begin t = Nach[t]->k; t -> stack;
просмотреть t; Nov[t] = false; end;
else //вершина t использована
stack -> t //удалить из стека верхний элемент
end;
end;
Здесь граф представлен списком инцидентности Nach[t], и k – определяет
информационную часть – номера вершин, а next – поле, указующее на
следующий элемент в списке, b – логическая вспомогательная величина.

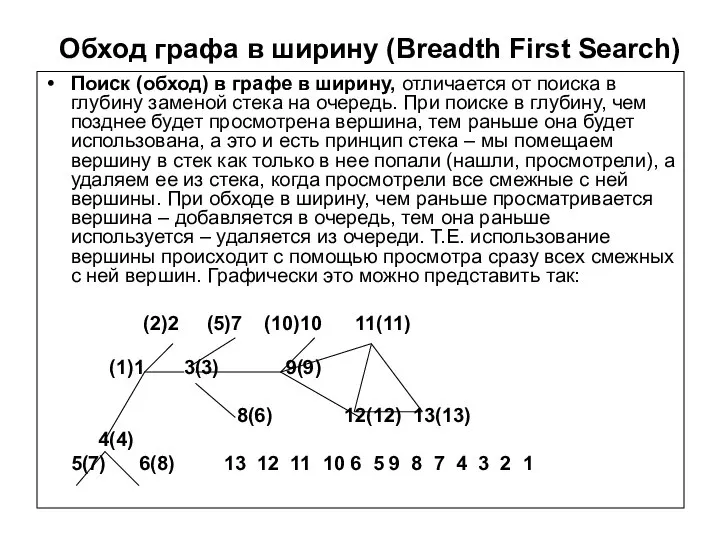
Обход графа в ширину (Breadth First Search)
Поиск (обход) в графе в ширину, отличается от поиска в глубину заменой стека на очередь. При поиске в глубину, чем позднее будет просмотрена вершина, тем раньше она будет использована, а это и есть принцип стека – мы помещаем вершину в стек как только в нее попали (нашли, просмотрели), а удаляем ее из стека, когда просмотрели все смежные с ней вершины. При обходе в ширину, чем раньше просматривается вершина – добавляется в очередь, тем она раньше используется – удаляется из очереди. Т.Е. использование вершины происходит с помощью просмотра сразу всех смежных с ней вершин. Графически это можно представить так:
(2)2 (5)7 (10)10 11(11)‏
(1)1 3(3) 9(9)
8(6) 12(12) 13(13)‏
4(4)
5(7) 6(8)‏ 1 2 3 4 7 8 9 5 6 10 11 12 13

Обход графа в ширину
Алгоритм обхода в ширину на псевдокоде можно записать так:
function BFS (v)‏
begin Queue = 0; v ->Queue;
Nov[v] = false;
while (queue <> 0) do
begin
Queue -> p; просмотреть p;
for ( u є Spisok[p]) do
if (Nov[u])‏
then
begin Nov[u] = false;
u -> Queue;
end;
end;
end;

Обход графа в ширину
Оба алгоритма могут использоваться для нахождения пути между данными вершинами u и v. Для этого достаточно начать обход, например, с вершины u и продолжать его до тех пор пока не будет просмотрена вершина v.
Достоинством обхода в глубину является тот факт, что в момент просмотра вершины v в стеке будет находиться последовательность вершин, определяющих путь от вершины u к вершине v, но недостатком этого алгоритма является то, что найденный путь может оказаться не кратчайшим.
Этого недостатка лишен алгоритм поиска в ширину.
Для нахождения кратчайшего пути из u в v необходимо ввести в рассмотрение глобальный массив, назовем его Pred и будем заполнять его во внутреннем цикле при просмотре очередной вершины, добавив строку Pred[u] = p;
…………………………
for ( u є Spisok[p]) do
if (Nov[u])‏
then
begin Nov[u] = false;
u -> Queue; Pred[u]=p;
end;

Представление графов в С/С++
Матрицу инциденции и матрицу смежности можно представить двумерным массивом целых элементов:
const int n= ,m= ;
int Matr_in[n][m];
Matr_sm[n][n];
Список инцидентности можно представить массивом указателей на односвязные списки:
struct tnode
{ int k;
next *tnode;
} Sp_in[n];
Здесь n – количество вершин в графе, а количество ребер не фиксируется, их можно добавлять и удалять динамически в процессе выполнения программы.