Содержание
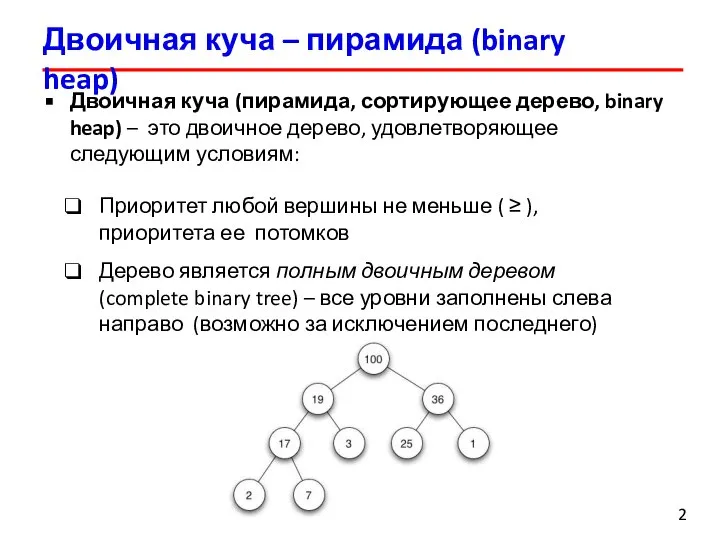
- 2. Двоичная куча – пирамида (binary heap) Двоичная куча (пирамида, сортирующее дерево, binary heap) – это двоичное
- 3. История появления Бинарная куча была Джоном Уильямом Джозефом Уильямсом в 1964 году как структура данных для
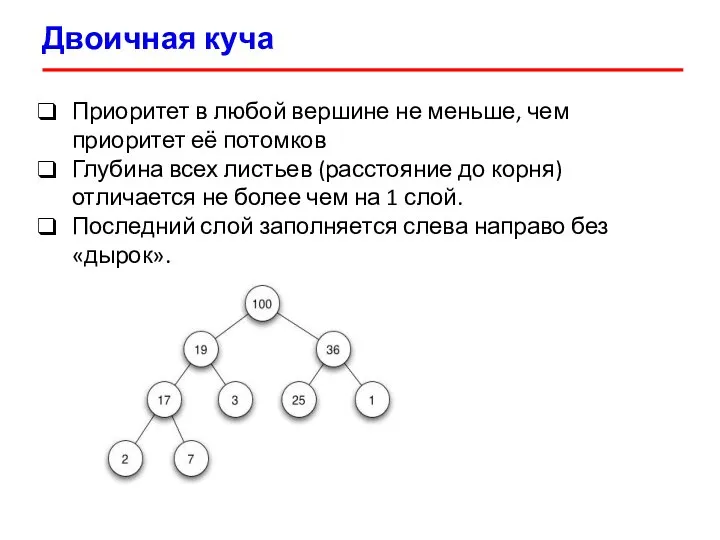
- 4. Двоичная куча Приоритет в любой вершине не меньше, чем приоритет её потомков Глубина всех листьев (расстояние
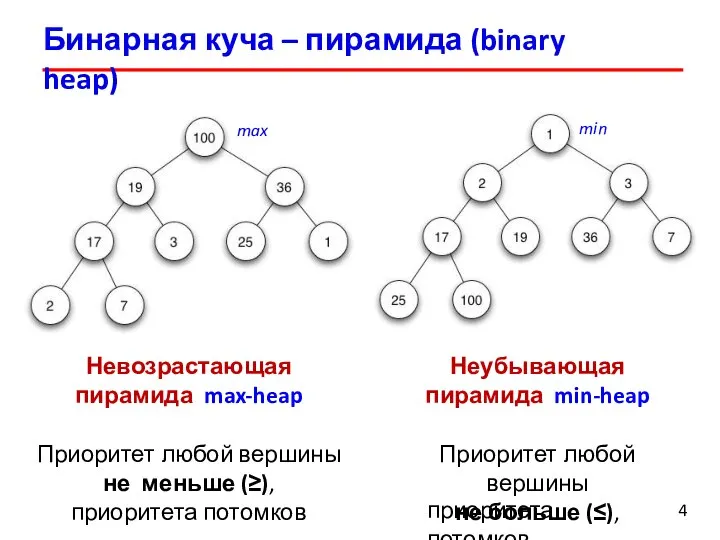
- 5. Бинарная куча – пирамида (binary heap) 4 Невозрастающая пирамида max-heap Приоритет любой вершины не меньше (≥),
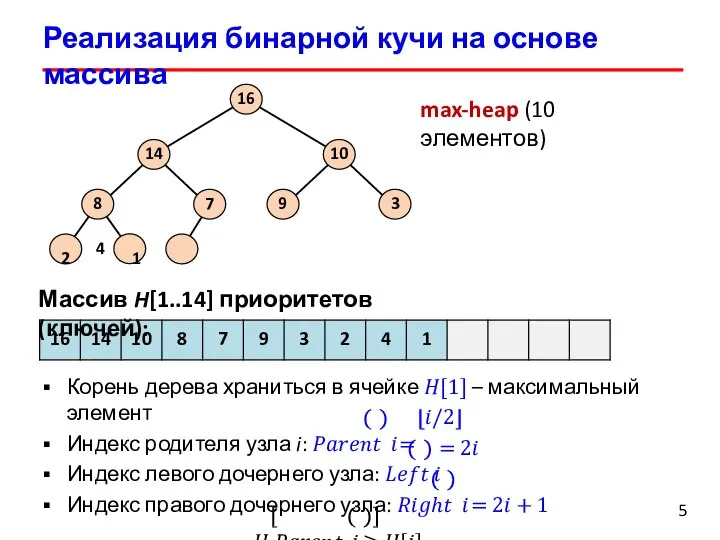
- 6. Реализация бинарной кучи на основе массива 5 7 8 2 4 1 9 3 14 10
- 7. Реализация бинарной кучи на основе массива /* Priority (key) */ /* Data */ struct heapnode {
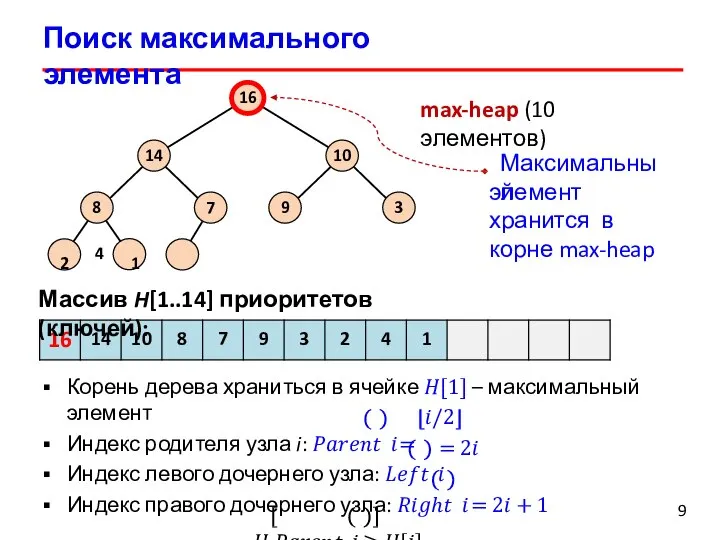
- 8. Поиск максимального элемента 9 7 8 2 4 1 9 3 14 10 16 max-heap (10
- 9. Вставка элемента в бинарную кучу 11 15 15 15 nnodes++; nodes[nnodes] = 15 15 15 >
- 10. Вставка элемента в бинарную кучу void addelem(int n) { int i, parent; i = HeapSize; h[i]
- 11. Поиск максимального элемента 10 struct heapnode *heap_max(struct heap *h) { if (h->nnodes == 0) return NULL;
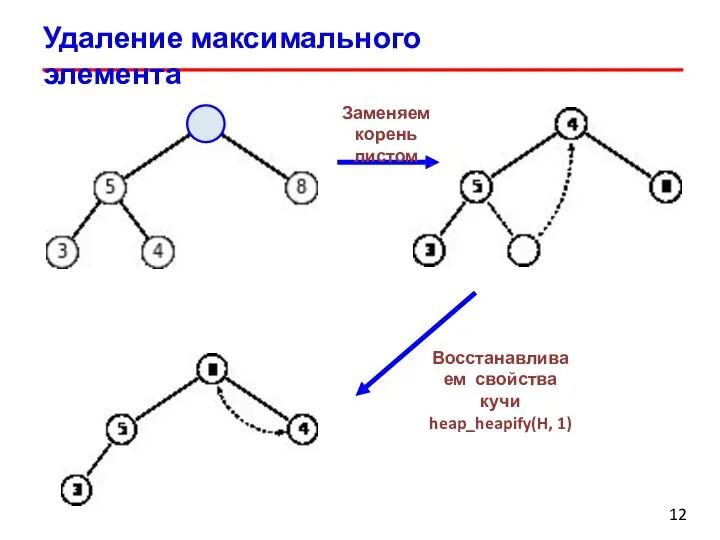
- 12. Удаление максимального элемента Заменяем корень листом Восстанавливаем свойства кучи heap_heapify(H, 1)
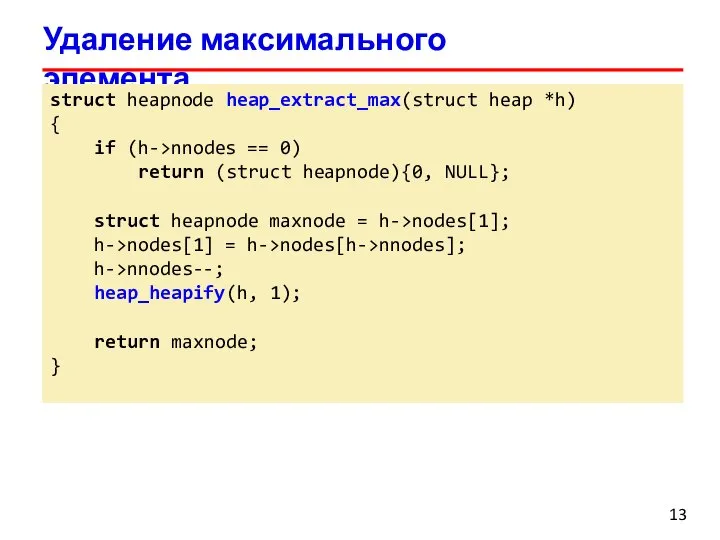
- 13. Удаление максимального элемента struct heapnode heap_extract_max(struct heap *h) { if (h->nnodes == 0) return (struct heapnode){0,
- 14. Удаление максимального элемента int getmax() { int x; x = h[0]; h[0] = h[HeapSize-1]; HeapSize--; heapify(0);
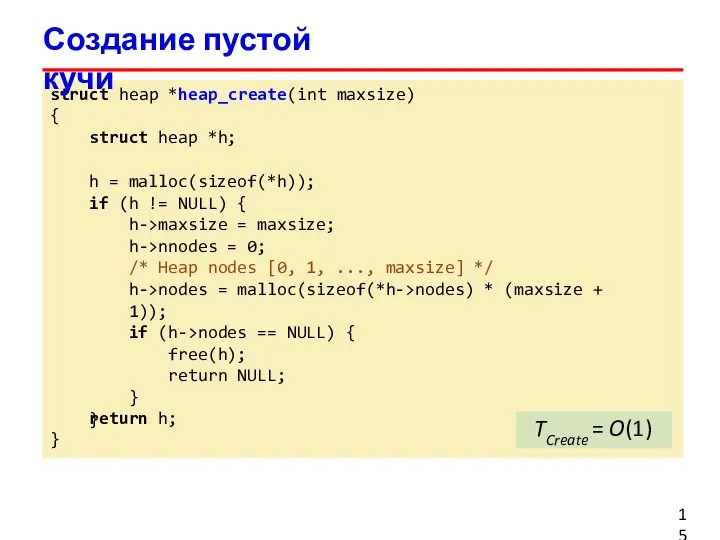
- 15. struct heap *heap_create(int maxsize) { struct heap *h; h = malloc(sizeof(*h)); if (h != NULL) {
- 16. void heap_free(struct heap *h) { free(h->nodes); free(h); } void heap_swap(struct heapnode *a, struct heapnode *b) {
- 17. Восстановление свойств кучи (max-heap) 5 1 void heap_heapify(struct heap *h, int index) { for (;;) {
- 18. int main() { struct heap *h; struct heapnode node; h = heap_create(100); node = heap_extract_max(h); printf("Item:
- 19. Изменение кучи
- 20. Увеличение ключа int heap_increase_key(struct heap *h, int index, int key) { if (h->nodes[index].key > key) return
- 21. Построение бинарной кучи Дан неупорядоченный массив A длины n Требуется построить из его элементов бинарную кучу
- 22. Построение бинарной кучи (v1) Дан неупорядоченный массив A длины n Требуется построить из его элементов бинарную
- 23. Построение бинарной кучи (v2) 23 Дан неупорядоченный массив A длины n Требуется построить из его элементов
- 24. Использование двоичной кучи
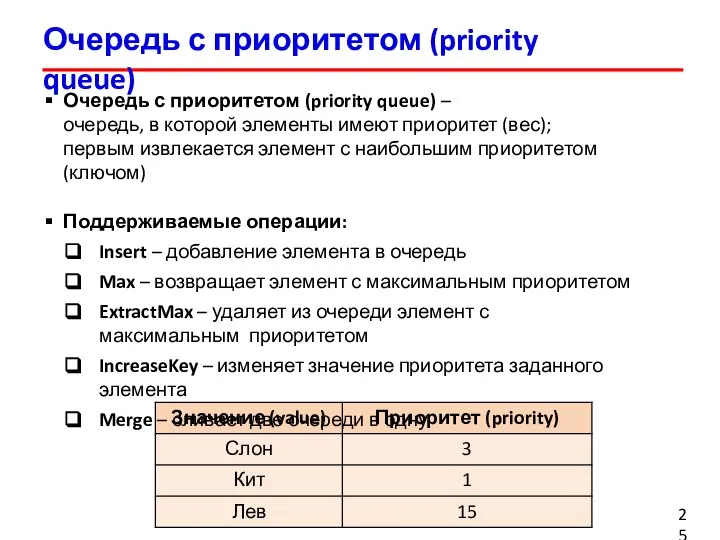
- 25. Очередь с приоритетом (priority queue) Очередь с приоритетом (priority queue) – очередь, в которой элементы имеют
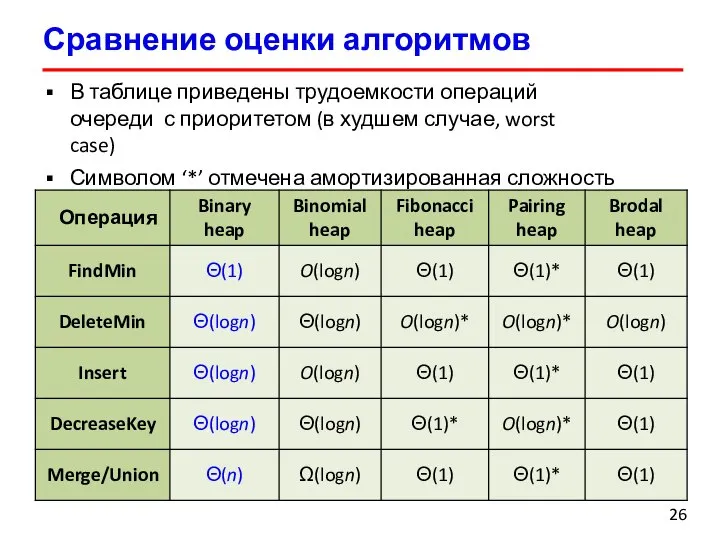
- 26. Сравнение оценки алгоритмов В таблице приведены трудоемкости операций очереди с приоритетом (в худшем случае, worst case)
- 27. Алгоритм Дейкстры Обозначим через n количество вершин, а через m — количество рёбер в графе G.
- 28. Сортировка на базе бинарной кучи На основе бинарной кучи можно реализовать алгоритм сортировки с вычислительной сложностью
- 29. Сортировка на базе бинарной кучи На основе бинарной кучи можно реализовать алгоритм сортировки с вычислительной сложностью
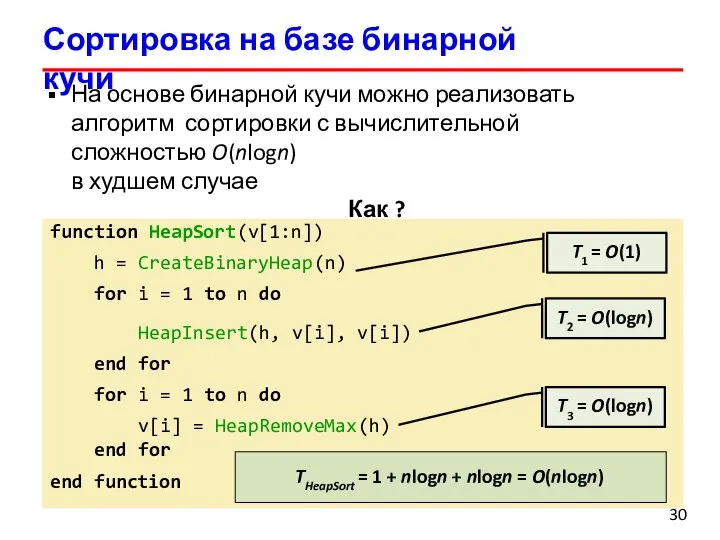
- 30. Сортировка на базе бинарной кучи На основе бинарной кучи можно реализовать алгоритм сортировки с вычислительной сложностью
- 31. Оценки работы алгоритма
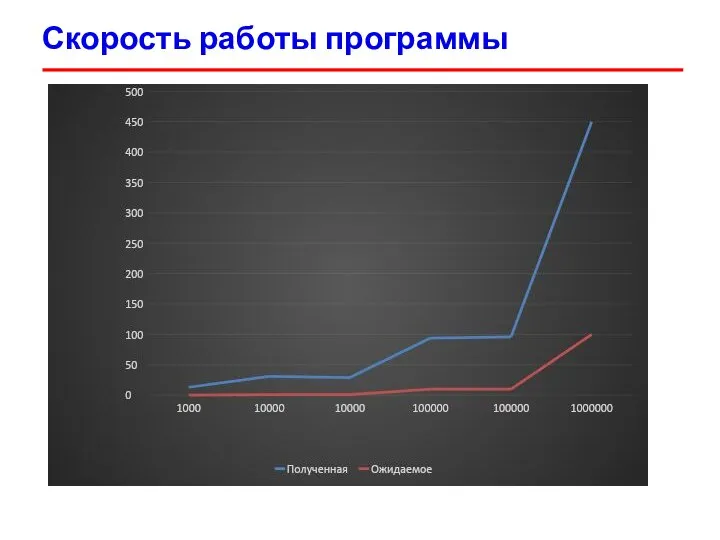
- 32. Скорость работы программы
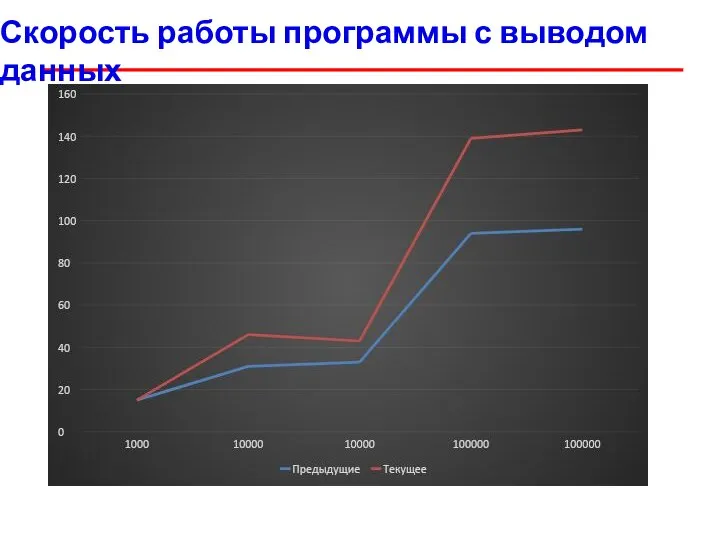
- 33. Скорость работы программы с выводом данных
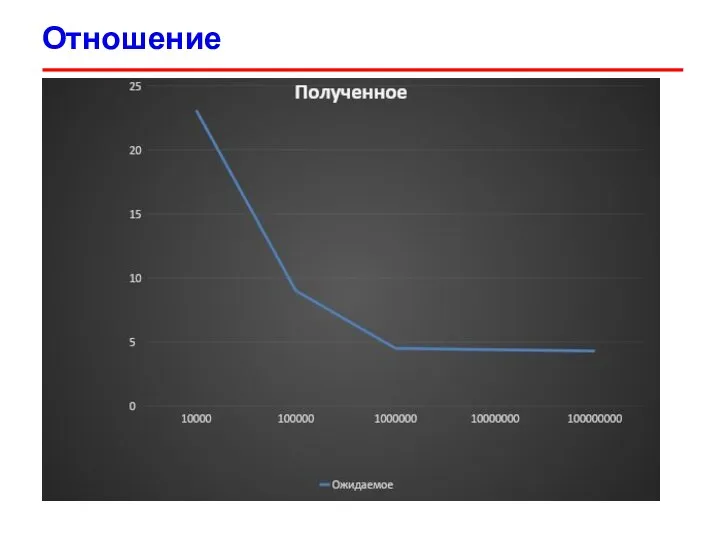
- 34. Отношение
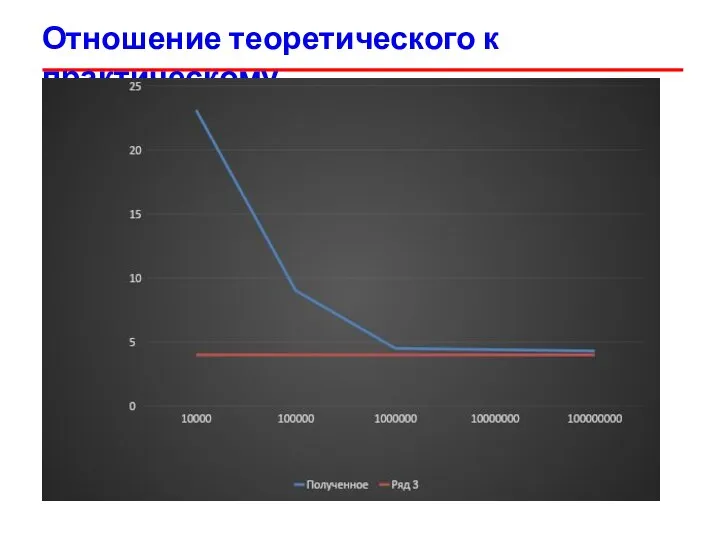
- 35. Отношение теоретического к практическому
- 37. Скачать презентацию


![Вставка элемента в бинарную кучу 11 15 15 15 nnodes++; nodes[nnodes] =](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/968046/slide-8.jpg)

![Удаление максимального элемента int getmax() { int x; x = h[0]; h[0]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/968046/slide-13.jpg)













 Тестовая программа по информатике
Тестовая программа по информатике Использование презентаций на уроках литературного чтения
Использование презентаций на уроках литературного чтения Blu-ray. Преимущества Blu-ray
Blu-ray. Преимущества Blu-ray Bilgisayar ağları ve iletişim. Ip adres tanimlamalari ve siniflari, alt ağlar, ipv6. (4.hafta)
Bilgisayar ağları ve iletişim. Ip adres tanimlamalari ve siniflari, alt ağlar, ipv6. (4.hafta) Лекция6
Лекция6 Турнир кибермании
Турнир кибермании Аппаратура информатизации образования
Аппаратура информатизации образования Концепция ERP-системы 1С:Управление предприятием
Концепция ERP-системы 1С:Управление предприятием Організація пам'яті комп'ютера. Прості схеми управління пам'яттю. Тема 3.1
Організація пам'яті комп'ютера. Прості схеми управління пам'яттю. Тема 3.1 Использование систем мгновенного обмена сообщениями в процессе иноязычной подготовки студентов на примере сервиса Discord
Использование систем мгновенного обмена сообщениями в процессе иноязычной подготовки студентов на примере сервиса Discord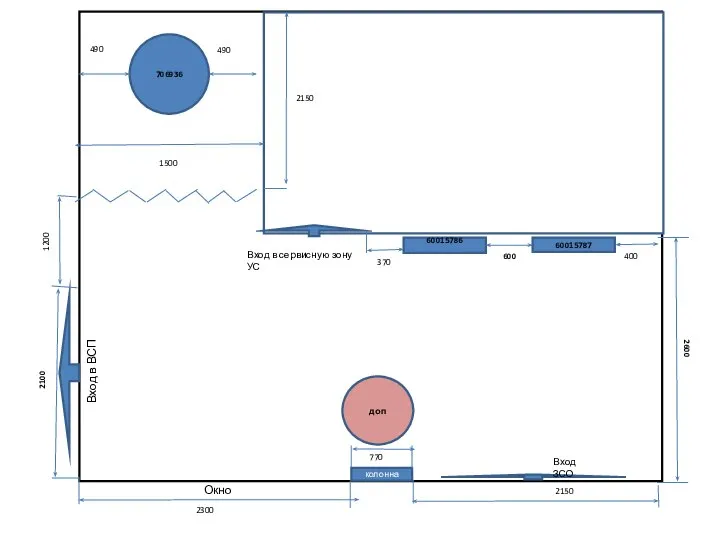 План зсо
План зсо лаб работа 1 базы данных
лаб работа 1 базы данных Web-программирование. Основы Node.js
Web-программирование. Основы Node.js Особенности текстов разных типов
Особенности текстов разных типов Разработка игры по технике безопасности на предприятии (организации)
Разработка игры по технике безопасности на предприятии (организации) Регистрация в Moodle: пошаговая инструкция
Регистрация в Moodle: пошаговая инструкция Способы взаимодействия с онлайн-аудиторией
Способы взаимодействия с онлайн-аудиторией Создание запросов в СУБД Access 2007
Создание запросов в СУБД Access 2007 Разумный подход к ресурсам
Разумный подход к ресурсам Tutoriel pour charger EV avec l’application E-Mobility Développé par SAP
Tutoriel pour charger EV avec l’application E-Mobility Développé par SAP Вычислительные системы, сети и телекоммуникации
Вычислительные системы, сети и телекоммуникации Электронная паспортизация музеев образовательных организаций. Портал Школьные музеи
Электронная паспортизация музеев образовательных организаций. Портал Школьные музеи Классификации ПО. Общие сведения
Классификации ПО. Общие сведения Альбом. Дипломное проектирование
Альбом. Дипломное проектирование Разработка тематического проекта Web-сайта различными инструментами
Разработка тематического проекта Web-сайта различными инструментами Индикаторы качества медицинской помощи. Новая модель премирования работников
Индикаторы качества медицинской помощи. Новая модель премирования работников Темы для самостоятельной работы. Развитие интернет технологий
Темы для самостоятельной работы. Развитие интернет технологий Программы для выполнения (поиск, максимальный и минимальный элементы)
Программы для выполнения (поиск, максимальный и минимальный элементы)