Функционалы Минковского цифровых пространств

Введение
Изучение функционалов Минковского на сегодняшний день актуально и востребовано, так как они являются достаточно точным инструментом моделирования и изучения пористых сред. Их можно использовать при срезах томографа любого черно-белого изображения объекта реального мира [1, 2, 3].
Для наиболее точного описания и дальнейшей характеристики пористой структуры используется двумерное цифровое пространство.
В данной работе изучается алгоритм вычисления некоторых функционалов Минковского для цифровых пространств. Таким образом, можно наиболее точно дать характеристику пористой структуре, имея только начальное бинарное изображение.

Понятие двумерного цифрового пространства

Двумерным цифровым пространством называют сетку, ячейки которой принимают значения: “0” - в ячейке нет элемента (белый цвет ячейки), “1” - в ячейке есть элемент (черный цвет ячейки). Тогда совокупность черных и белых ячеек образует изображение в двумерном цифровом пространстве.
Двумерное цифровое пространство задается как совокупность 0 и 1 (матричное представление двумерного цифрового пространства).
Элементы данного пространства называются пикселями в размерности 2 и вокселями в размерности 3.

Понятие 4-связности и 8-связности

Разница между типами связности
8 - связность: 4 - связность:
Каждый пиксель может иметь не Каждый пиксель имеет не
более 8 соседей. При таком способе более 4 соседей. Соседом
соседом считается тот пиксель, между считается тот пиксель, между
которым есть общая вершина или ребро которым есть общее ребро.
с рассматриваемым пикселем.

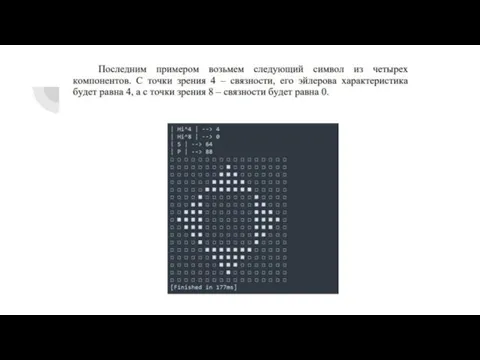
Вычисление эйлеровой характеристики цифровых пространств

Заключение
Мы проверили работу алгоритма на наглядных примерах бинарных изображений и убедились в точности вычислений. Алгоритм был разработан с использованием результатов работ [4, 5].
Дальнейшее развитие работы предполагает написание алгоритма для большей размерности пространства.