ГРАФИКА_анимация_LAZARUS_Мартынюк

ПРЕОБРАЗОВАНИЕ ИЗОБРАЖЕНИЙ
Все основные изменения рисунков можно выполнить с помощью трех базовых операций:
переноса изображения с одного места на другое (перемещения);
увеличения или уменьшения размеров отображаемого рисунка (масштабирования);
изменения ориентации рисунка (вращения).

ПЕРЕМЕЩЕНИЕ
x,y
x1,y1
dx
dy
x1=x+dx
y1=y+dy
dx и dy задают скорости перемещения точки
dx>0 - перемещение точки по горизонтали вправо
dx<0 - по горизонтали влево
dy>0 - перемещение по вертикали вниз
dy<0 - по вертикали вверх
При написании программы не надо вводить дополнительные переменные x1 и y1.
x=x+dx
y=y+dy

МАСШТАБИРОВАНИЕ
xm,ym
x,y
Необходимо задать:
1. коэффициенты масштабирования kx и ky.
2. координаты точки, относительно которой производится масштабирование xm и ym (центр масштабирования).
Масштабирование может быть:
однородным (коэффициенты масштабирования по горизонтали и вертикали одинаковы и пропорции объекта сохраняются)
неоднородным (коэффициенты масштабирования неодинаковы по горизонтали и вертикали и пропорции объекта не сохраняются)
Координаты точки (Х,Y) после масштабирования рисунка определяются по формулам:
x=xm*(1-kx)+kx*x
y=ym*(1-ky)+ky*y
При KX>1 и KY>1 рисунок увеличивается в размерах и удаляется от центра масштабирования;
при KX<1 и KY<1 рисунок уменьшается в размерах и приближается к центру масштабирования

ВРАЩЕНИЕ
x,y
x1,y1
xv,yv
Необходимо задать:
1. Угловую скорость вращения dfi (положительное направление поворота против часовой стрелки, отрицательное - по часовой стрелке. Задается в радианах.
2. координаты точки, относительно которой производится поворот xv и yv (центр вращения).
dfi
Координаты точки (x1,y1) после поворота рисунка определяются по формулам:
x1=xv+(x-xv)*cos(dfi)+(y-yv)*sin(dfi)
y1=yv+(y-yv)*cos(dfi)-(x-xv)*sin(dfi)
Убрать x1 и y1 просто так нельзя, так как в первой формуле X перевычисляется. А во второй формуле надо использовать старое значение x. Кроме этого, при многократном перевычислении координат при округлении ошибка будет накапливаться, и рисунок будет искажаться. Поэтому надо сохранить координаты начального положения рисунка, и вычислять угол, на который повернут рисунок от начального положения.
fi=fi+dfi
x=xv+(xn-xv)*cos(fi)+(yn-yv)*sin(fi)
y=yv+(yn-yv)*cos(fi)-(xn-xv)*sin(fi)

ФОРМИРОВАНИЕ ДВИЖУЩИХСЯ ИЗОБРАЖЕНИЙ
При создании движущихся изображений используются рассмотренные геометрические преобразования: перемещение, масштабирование и поворот. Принцип создания движущихся изображений состоит в том, что изображение высвечивается на экране, затем стирается, выполняются необходимые преобразования и опять высвечивается изображение, но уже преобразованное. При многократном повторении этой процедуры получается движущееся изображение.
Все программы, позволяющие воспроизводить движущееся изображение, имеют следующую особенность. Поскольку человеческий глаз обладает определенной инерционностью восприятия, то нельзя нарисовать изображение, затем сразу же стереть его и нарисовать новое изображение. Перед стиранием изображения необходимо предусмотреть задержку. Интервал времени, в течение которого высвечивается изображение, должен быть больше, чем интервал времени, в течение которого изображение отсутствует.
Элемент управления Timer
Движение моделируется с помощью невизуального компонента Timer.
Он применяется для повторения выполнения заданных алгоритмов через определенные интервалы времени.
Основные свойства:
Interval - определяет интервал времени, через который Timer должен «включаться» и выполнять заложенный алгоритм. Чем меньше Interval, тем быстрее будет двигаться фигура.
Enabled – включает Timer (если Enabled = False, Timer выключен).

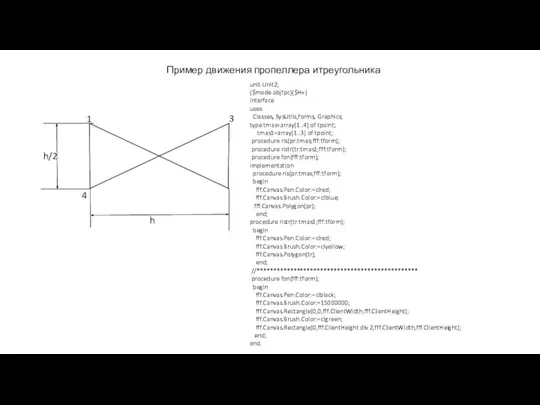
Пример движения пропеллера итреугольника
h
h/2
4
1
3
unit Unit2;
{$mode objfpc}{$H+}
interface
uses
Classes, SysUtils,forms, Graphics;
type tmas=array[1..4] of tpoint; tmas1=array[1..3] of tpoint;
procedure ris(pr:tmas;fff:tform);
procedure ristr(tr:tmas1;fff:tform);
procedure fon(fff:tform);
implementation
procedure ris(pr:tmas;fff:tform);
begin
fff.Canvas.Pen.Color:=clred;
fff.Canvas.Brush.Color:=clblue;
fff.Canvas.Polygon(pr);
end;
procedure ristr(tr:tmas1;fff:tform);
begin
fff.Canvas.Pen.Color:=clred;
fff.Canvas.Brush.Color:=clyellow;
fff.Canvas.Polygon(tr);
end;
//************************************************
procedure fon(fff:tform);
begin
fff.Canvas.Pen.Color:=clblack;
fff.Canvas.Brush.Color:=15000000;
fff.Canvas.Rectangle(0,0,fff.ClientWidth,fff.ClientHeight);
fff.Canvas.Brush.Color:=clgreen;
fff.Canvas.Rectangle(0,fff.ClientHeight div 2,fff.ClientWidth,fff.ClientHeight);
end;
end.

Перемещение пропеллера
var
dfi,fi, k :real;
pr,prn:tmas;
xv, yv,xm,ym, xc,yc,h, kol : Integer;
dx, dy: Integer;
tr,trn:tmas1;
procedure TForm1.Button1Click(Sender: TObject); //Перемещение
begin
xc:=form1.ClientWidth div 4;
yc:=form1.ClientHeight div 4;
h:=yc div 2;
pr[1].X:= xc - h div 2; pr[1].Y:= yc - h div 4;
pr[2].X:= xc + h div 2 ; pr[2].y:= yc + h div 4;
pr[3].X:= xc + h div 2 ; pr[3].Y:= yc - h div 4;
pr[4].X:= xc - h div 2; pr[4].Y:= yc + h div 4;
ris(pr,form1);
dx:= 2;
dy:= 2;
Timer1.Enabled:= True;
end;
procedure TForm1.Timer1Timer(Sender: TObject); //Перемещение
var i:integer;
begin
form1.Refresh;
for i:=1 to 4 do
begin
pr[i].x:=pr[i].x+dx;
pr[i].y:=pr[i].y+dy;
end;
ris(pr,form1);
if (pr[4].y>form1.ClientHeight)or(pr[1].y<0) then dy:=-dy;
if (pr[2].x>form1.ClientWidth)or(pr[1].x<0) then dx:=-dx;
end;

Масштабирование пропеллера
procedure TForm1.Button2Click(Sender: TObject); //Масштабирование
begin
xc:=form1.ClientWidth div 4;
yc:=form1.ClientHeight div 4;
h:=yc; // xc:=(form1.ClientWidth div 4)*3;
//yc:=(form1.ClientHeight div 4)*3;
pr[1].X:= xc - h div 2; pr[1].Y:= yc - h div 4;
pr[2].X:= xc + h div 2 ; pr[2].y:= yc + h div 4;
pr[3].X:= xc + h div 2 ; pr[3].Y:= yc - h div 4;
pr[4].X:= xc - h div 2; pr[4].Y:= yc + h div 4;
ris(pr,form1);
xm:=form1.ClientWidth;
ym:=form1.ClientHeight;
k:=0.98;
//k:=1.02;
Timer2.Enabled:= True;
end;
procedure TForm1.Timer2Timer(Sender: TObject); //Масштабирование
var i:integer;
begin
form1.Refresh;
for i:=1 to 4 do
begin
pr[i].x:=round(k*pr[i].x+(1-k)*xm);
pr[i].y:=round(k*pr[i].y+(1-k)*ym);
end;
ris(pr,form1);
end;

Вращение пропеллера
procedure TForm1.Button3Click(Sender: TObject); //Вращение
begin
xc:=form1.ClientWidth div 4;
yc:=form1.ClientHeight div 2-20;
h:=yc div 2;
pr[1].X:= xc - h div 2; pr[1].Y:= yc - h div 4;
pr[2].X:= xc + h div 2 ; pr[2].y:= yc + h div 4;
pr[3].X:= xc + h div 2 ; pr[3].Y:= yc - h div 4;
pr[4].X:= xc - h div 2; pr[4].Y:= yc + h div 4;
prn:=pr;
ris(pr,form1);
dfi:= -PI / 18;
fi:=0;
kol:= 0;
xv:= 200;
yv:= 200;
Timer3.Enabled:= True;
end;
procedure TForm1.Timer3Timer(Sender: TObject); // Вращение
var i:integer;
begin
fon(form1);
fi:=fi+dfi;
for i:=1 to 4 do
begin
pr[i].x:=round(xv+(prn[i].x-xv)*cos(fi)+(prn[i].y-yv)*sin(fi));
pr[i].y:=round(yv+(prn[i].y-yv)*cos(fi)-(prn[i].x-xv)*sin(fi));
end;
ris(pr,form1);
kol:=kol+1;
if (kol mod 18)=0 then dfi:=-dfi;
end;

Сложное движение пропеллера
procedure TForm1.Button4Click(Sender: TObject); // Сложное
begin
xc:=form1.ClientWidth div 4;
yc:=form1.ClientHeight div 4;
h:=yc div 2;
pr[1].X:= xc - h div 2; pr[1].Y:= yc - h div 4;
pr[2].X:= xc + h div 2 ; pr[2].y:= yc + h div 4;
pr[3].X:= xc + h div 2 ; pr[3].Y:= yc - h div 4;
pr[4].X:= xc - h div 2; pr[4].Y:= yc + h div 4;
prn:=pr;
ris(pr,form1);
dx:= 2;
dy:= 2;
dfi:= -PI / 18;
fi:=0;
xv:=xc;
yv:=yc;
//xv:= pr[2].X;
//yv:= pr[2].Y;
// xv:= 200;
// yv:= 200;
Timer4.Enabled:= True;
end;
procedure TForm1.Timer4Timer(Sender: TObject); // Сложное
var i:integer;
begin
fon(form1);
for i:=1 to 4 do
begin
prn[i].x:=prn[i].x+dx;
prn[i].y:=prn[i].y+dy;
end;
xv:=xv+dx;
yv:=yv+dy;
fi:=fi+dfi;
for i:=1 to 4 do
begin
pr[i].x:=round(xv+(prn[i].x-xv)*cos(fi)+(prn[i].y-yv)*sin(fi));
pr[i].y:=round(yv+(prn[i].y-yv)*cos(fi)-(prn[i].x-xv)*sin(fi));
end;
ris(pr,form1);
end;