Графы атак. Достижимость в графах

План
1. Понятие графа атак.
2. Достижимость в графах.
3. Алгоритмы построения матриц достижимости

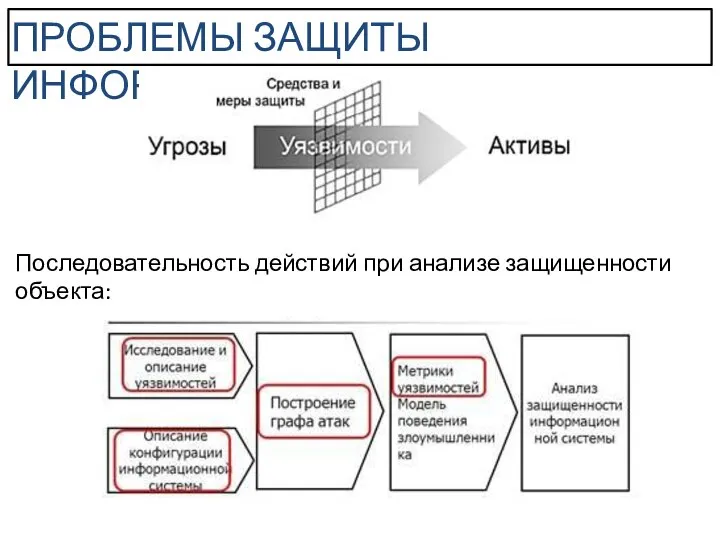
ПРОБЛЕМЫ ЗАЩИТЫ ИНФОРМАЦИИ
Последовательность действий при анализе защищенности объекта:

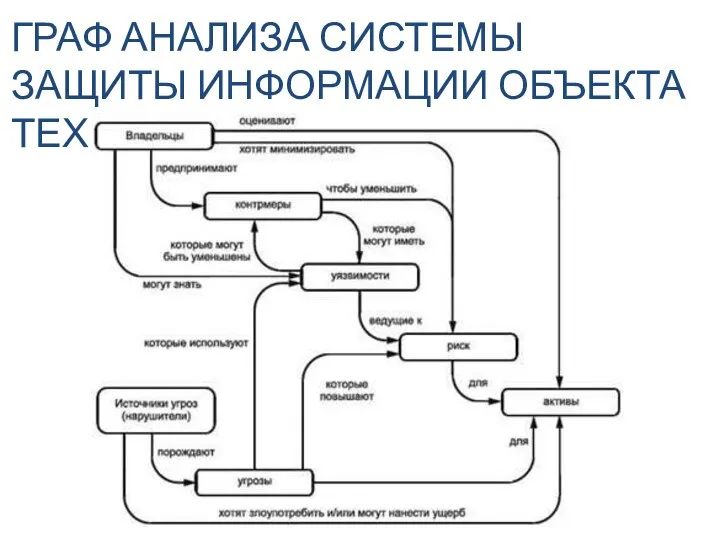
ГРАФ АНАЛИЗА СИСТЕМЫ ЗАЩИТЫ ИНФОРМАЦИИ ОБЪЕКТА ТЕХНИКИ

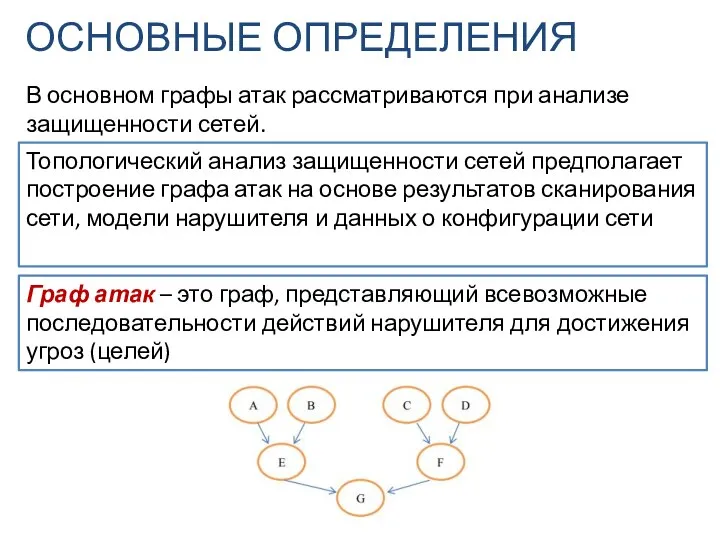
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
Граф атак – это граф, представляющий всевозможные последовательности действий нарушителя для достижения угроз (целей)
Топологический анализ защищенности сетей предполагает построение графа атак на основе результатов сканирования сети, модели нарушителя и данных о конфигурации сети
В основном графы атак рассматриваются при анализе защищенности сетей.

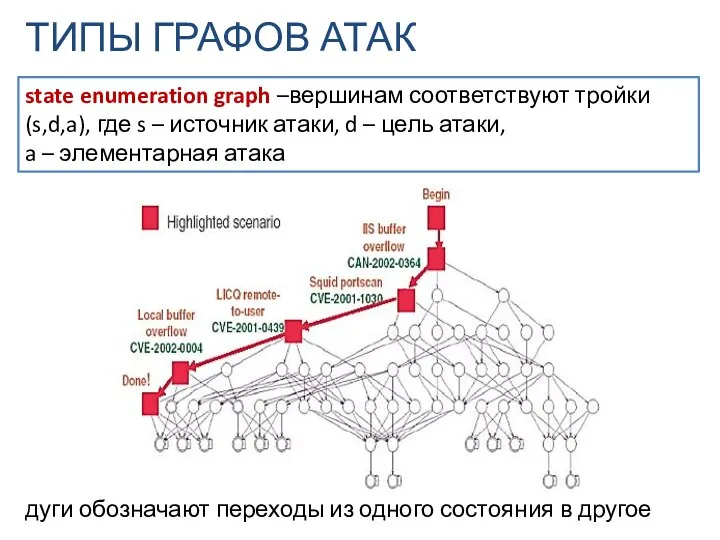
ТИПЫ ГРАФОВ АТАК
дуги обозначают переходы из одного состояния в другое
state enumeration graph –вершинам соответствуют тройки (s,d,a), где s – источник атаки, d – цель атаки,
a – элементарная атака

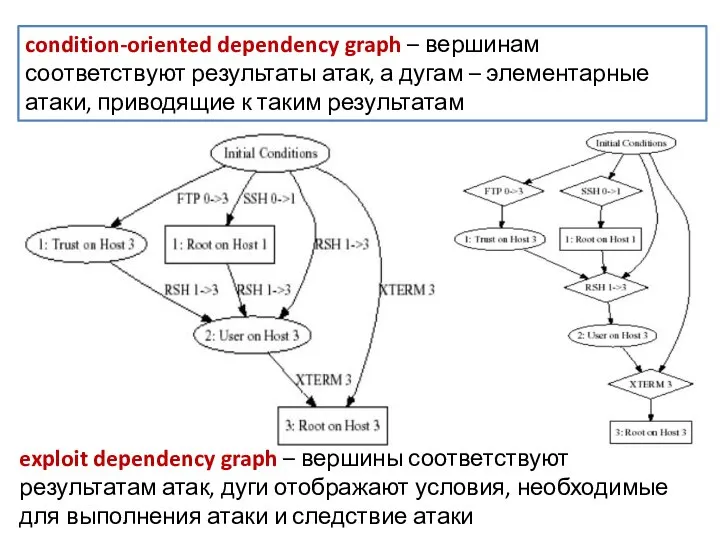
condition-oriented dependency graph – вершинам соответствуют результаты атак, а дугам – элементарные атаки, приводящие к таким результатам
exploit dependency graph – вершины соответствуют результатам атак, дуги отображают условия, необходимые для выполнения атаки и следствие атаки

Под элементарной атакой (atomic attack) понимают использование нарушителем уязвимости.
Граф может быть моделью организации, в которой люди представлены вершинами, а дуги интерпретируют каналы связи. При рассмотрении такой модели можно поставить вопрос, может ли информация от одного лица хi быть передана другому лицу хj
т. е. существует ли путь, идущий от вершины хi к вершине хj. Если такой путь существует, то говорят, что вершина хj достижима из вершины хi. Можно интересоваться достижимостью вершины хj из вершины хi только на таких путях, длины которых не превосходят заданной величины или длина которых меньше наибольшего числа вершин в графе и т. д.

Перед построением графа атак необходимо построить матрицу достижимости
Матрица достижимости может рассчитываться между объектами сети, или между объектами сети и источниками угроз. При расчете матрицы достижимости учитываются следующие особенности:
- динамическая маршрутизация : объект считается достижимым, если он достижим хотя бы по одному маршруту;
- возможность наличия нескольких оконечных точек для объекта (источника угроз) : угроза считается достижимой, если она достижима хотя бы на одной оконечной точке;
- при расчете матрицы учитываются возможности преобразования адресов источника и получателя (источника угроз и узла сети).
Граф атак может строиться в одном из следующих режимов:
- из одного объекта-источника атаки;
- конечного набора объектов-источников атаки

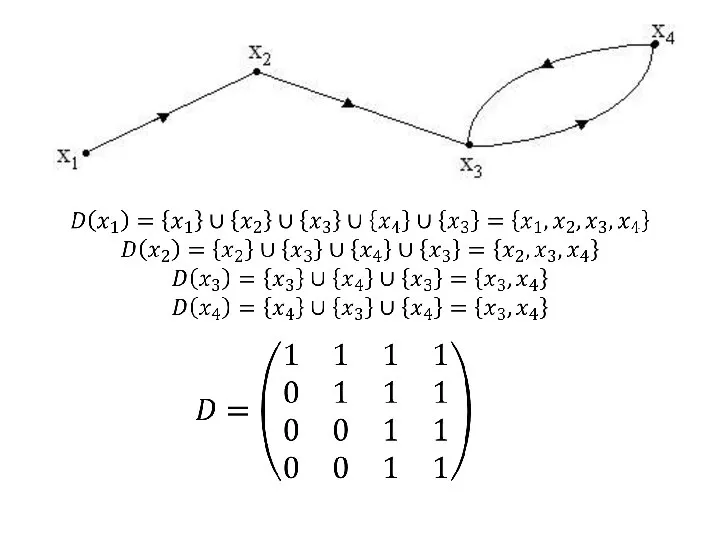
ПОНЯТИЕ ДОСТИЖИМОСТИ

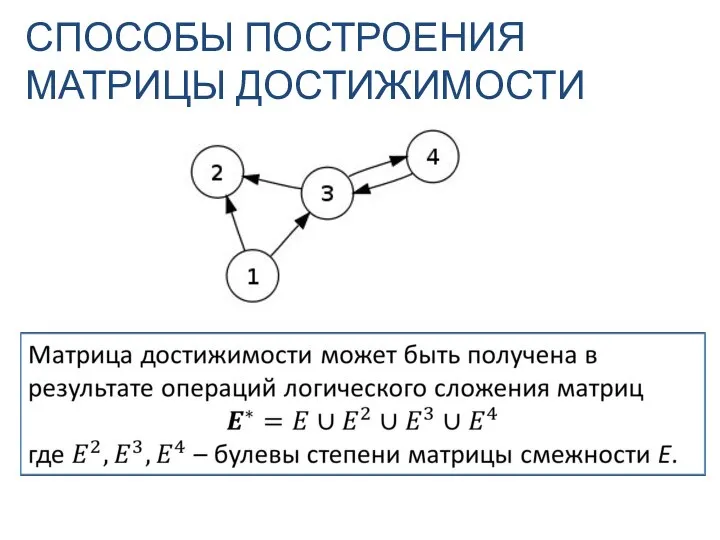
СПОСОБЫ ПОСТРОЕНИЯ МАТРИЦЫ ДОСТИЖИМОСТИ

const m=5; p=5; n=5;
var
e: array [1..m,1..p] of real;
b: array [1..p,1..n] of real;
c: array [1..m,1..n] of real;
s: Real;
i, j, k: Integer;
begin
...
for i:=1 to m do
for j:=1 to n do begin
s:=0; for k:=1 to p do
s:=s+e[i,k]*b[k,j];
c[i,j]:=s;
end;
...
end.

const m=5; p=5; n=5;
var
e: array [1..m,1..m] of integer;
// b: array [1..p,1..n] of integer;
c: array [1..m,1..m] of integer;
s: integer;
i, j, k: Integer;
begin
...
for i:=1 to m do
for j:=1 to n do begin
s:=0; for k:=1 to p do
s:=s+e[i,k]*e[k,j];
c[i,j]:=s;
end;
...
end.

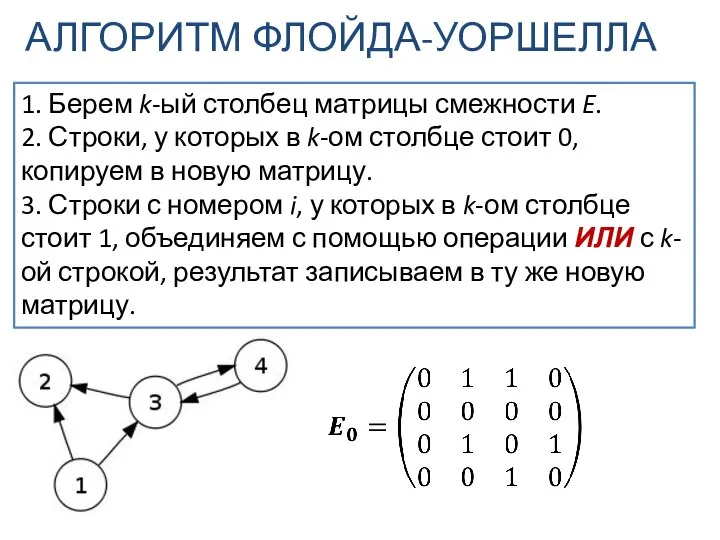
АЛГОРИТМ ФЛОЙДА-УОРШЕЛЛА
1. Берем k-ый столбец матрицы смежности E.
2. Строки, у которых в k-ом столбце стоит 0, копируем в новую матрицу.
3. Строки с номером i, у которых в k-ом столбце стоит 1, объединяем с помощью операции ИЛИ с k-ой строкой, результат записываем в ту же новую матрицу.

Вычисляем матрицу E1. Учитывая первый шаг, рассматриваем 1-ый столбец матрицы E0. Следуя указаниям шага 2, скопируем строки матрицы Е0, в первом столбце которой стоят 0:
В первом столбце единиц нет. Переходим к рассмотрению второго столбца и вычислению матрицы E2. Рассчитываем значения в строке 1-ой и 3-ей, выполняя дизъюнкцию k-ой строки (второй) со строками, у которых на k-ом месте стоит 1

Вычисляем матрицу E3. Рассматриваем 3-ий столбец матрицы E2. Копируем строки, у которых в 3-ем столбце 0: вторую и третью Рассчитываем значения в строке 1-ой и 4-ой, выполняя дизъюнкцию k-ой строки (третьей) со строками, у которых на k-ом месте стоит 1. Получаем матрицу E3:
Вычисляем матрицу E4. Рассматриваем 4-ый столбец матрицы E3. Копируем строки, у которых в 4-ом столбце 0: вторую. Рассчитываем значения в строке 1-ой, 3-ей и 4-ой, выполняя дизъюнкцию k-ой строки (четвертой) со строками, у которых на k-ом месте стоит 1. Полученная матрица является матрицей достижимости – E*

АЛГОРИТМ ФЛОЙДА-УОРШЕЛЛА: программная реализация
расчет кратчайших путей в графе
for k = 1 to n
for i = 1 to n
for j = 1 to n
W[i,j] = min(W[i,j], W[i,k] + W[k,j])
Для нахождения матрицы достижимости оператор min заменяется дизъюнкцией, сложение заменяется конъюнкцией
for k = 1 to n
for i = 1 to n
for j = 1 to n
W[i,j] = W[i,j] or (W[i,k] and W[k,j])

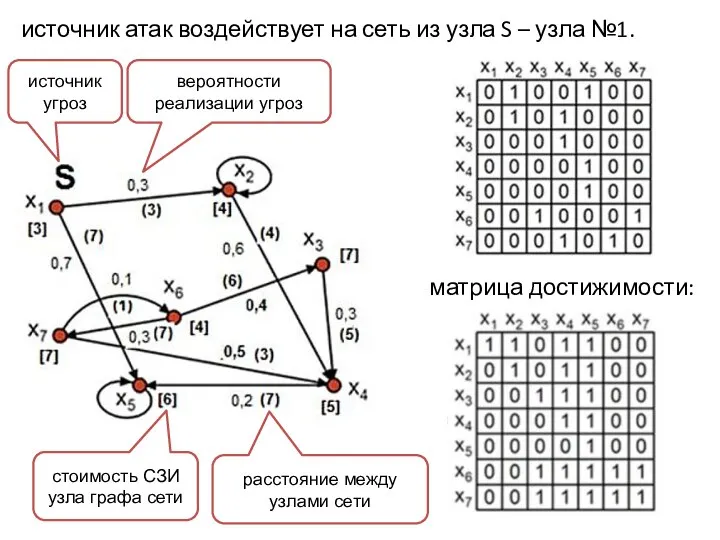
источник атак воздействует на сеть из узла S – узла №1.
источник угроз
вероятности реализации угроз
расстояние между узлами сети
стоимость СЗИ узла графа сети
матрица достижимости:

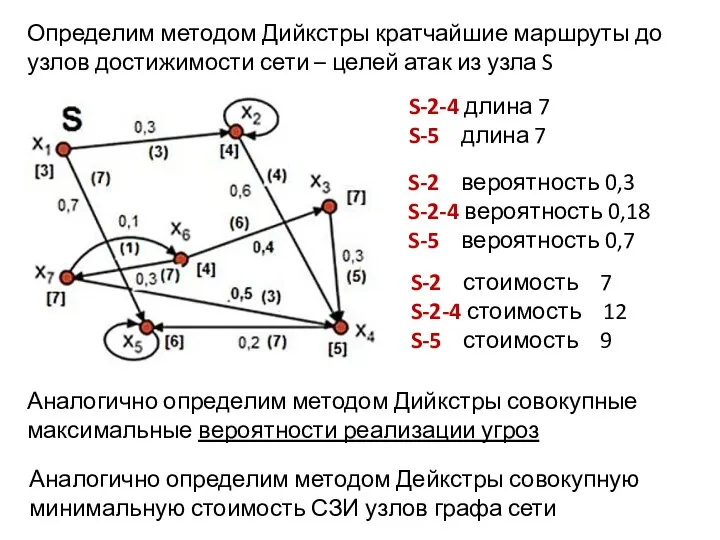
Определим методом Дийкстры кратчайшие маршруты до узлов достижимости сети – целей атак из узла S
S-2-4 длина 7
S-5 длина 7
Аналогично определим методом Дийкстры совокупные максимальные вероятности реализации угроз
S-2 вероятность 0,3
S-2-4 вероятность 0,18
S-5 вероятность 0,7
S-2 стоимость 7
S-2-4 стоимость 12
S-5 стоимость 9
Аналогично определим методом Дейкстры совокупную минимальную стоимость СЗИ узлов графа сети

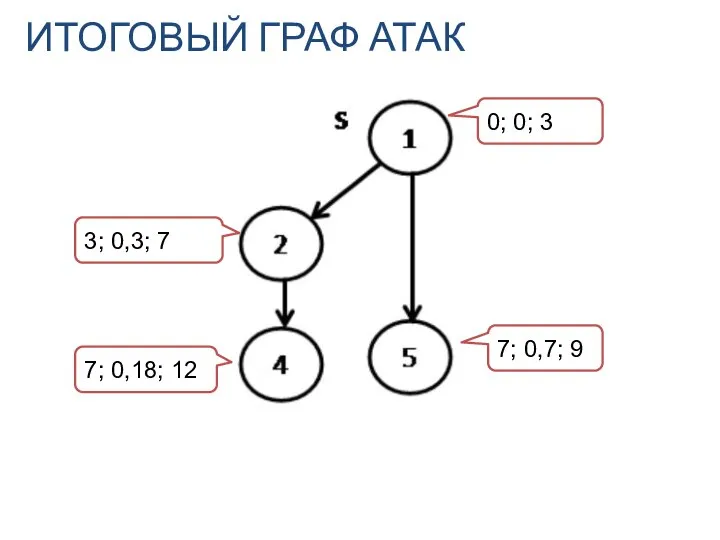
0; 0; 3
7; 0,18; 12
3; 0,3; 7
7; 0,7; 9
ИТОГОВЫЙ ГРАФ АТАК

Вопросы
1. Опишите последовательность действий при анализе защищенности объекта.
2. Дайте определение графа атак.
3. Какие виды графов атак вы знаете?
4. Определение матрицы достижимости.
5. Определение матрицы контрдостижимости.
6. Опишите матричный способ нахождения матрицы достижимости.
7. Опишите алгоритм Флойда-Уоршелла.

Источники информации
Программирование, компьютеры и сети https://progr-system.ru/