Характеристика алгоритмической сложности. Понятие и свойства алгоритмической сложности

АЛГОРИТМИЧЕСКАЯ СЛОЖНОСТЬ
связана с тем, насколько быстро или медленно работает конкретный алгоритм. Мы определяем сложность как числовую функцию T(n) - время против входного размера n. Мы хотим определить время, затраченное алгоритмом, не завися от деталей реализации. Но T(n) зависит от реализации. Данный алгоритм будет занимать различное количество времени на одних и тех же входах в зависимости от таких факторов, как: скорость процессора, набор команд, скорость диска, версия и тип компилятора и т. д. Обходной путь - асимптотически оценивать эффективность каждого алгоритма. Мы будем измерять время T(n) как количество элементарных "шагов" (определенных любым образом), при условии, что каждый такой шаг занимает постоянное время.

АСИМПТОТИЧЕСКИЕ ОБОЗНАЧЕНИЯ
Целью вычислительной сложности является классификация алгоритмов в соответствии с их производительностью. Мы представим функцию времени T(n), используя нотацию "big-O" для выражения сложности времени выполнения алгоритма. Например, следующее утверждение
говорит, что алгоритм имеет квадратичную сложность по времени.

ОПРЕДЕЛЕНИЕ "BIG O"
Для любых монотонных функций f(n) и g(n) от целых положительных чисел до целых положительных чисел говорят, что f(n) = O(g(n)), когда существуют такие константы c > 0 и n0 > 0, так что
Интуитивно это означает, что функция f(n) не растет быстрее, чем g(n), или что функция g(n) является верхней границей для f(n) для всех достаточно больших n → ∞

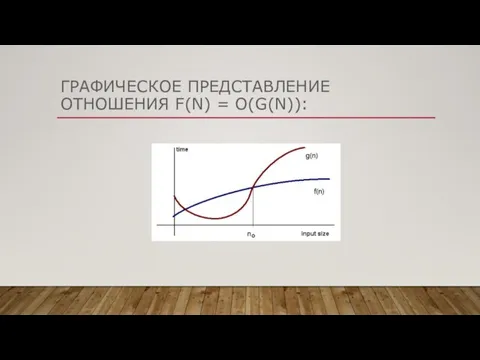
ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ОТНОШЕНИЯ F(N) = O(G(N)):

ПРИМЕРЫ:
"big-O" нотация не симметрична: n = O(n2) но n2 ≠ O(n).

ПОСТОЯННОЕ ВРЕМЯ: O(1)
Говорят, что алгоритм работает за постоянное время, если ему требуется одинаковое количество времени независимо от размера ввода. Примеры:
массив: доступ к любому элементу
стек фиксированного размера: методы push и pop
очередь фиксированного размера: методы enqueue и dequeue

ЛИНЕЙНОЕ ВРЕМЯ: O(N)
Говорят, что алгоритм работает за линейное время, если его выполнение по времени прямо пропорционально размеру ввода, то есть время увеличивается линейно с увеличением размера ввода. Примеры:
массив: линейный поиск, обход, нахождение минимума
ArrayList: метод contains
очередь: метод contains

ЛОГАРИФМИЧЕСКОЕ ВРЕМЯ: O(LOG N)
Говорят, что алгоритм работает за логарифмическое время, если его время выполнения пропорционально логарифму размера ввода. Пример:
бинарный поиск

КВАДРАТИЧНОЕ ВРЕМЯ: O(N*N)
Говорят, что алгоритм работает за квадратичное время, если его время выполнения пропорционально квадрату размера ввода. Примеры:
сортировка по пузырькам, сортировка по выделению, сортировка по вставке

ОПРЕДЕЛЕНИЕ ПОНЯТИЯ "BIG OMEGA"
Нам нужны обозначения для нижней границы. В этом случае используется заглавная omega Ω нотация. Мы говорим, что f(n) = Ω(g(n)), когда существует постоянная c, для которой f(n) ≥ c * g(n) для всех достаточно больших n. Примеры:

ОПРЕДЕЛЕНИЕ ПОНЯТИЯ "BIG THETA"
Чтобы измерить сложность конкретного алгоритма, нужно найти верхнюю и нижнюю границы. В этом случае используется новая запись. Мы говорим, что f(n) = Θ(g(n)) тогда и только тогда, когда f(n) = O(g(n)) и f(n) = Ω(g(n)). Примеры:

АНАЛИЗ АЛГОРИТМОВ
Наихудшая сложность алгоритма во время выполнения - это функция, определяемая максимальным количеством шагов, сделанных для любого экземпляра размера a.
наилучшая сложность алгоритма во время выполнения - это функция, определяемая минимальным числом шагов, предпринимаемых для любого экземпляра размера a.
средняя сложность времени выполнения алгоритма - это функция, определяемая средним числом шагов, предпринятых для любого экземпляра размера a.
Амортизированная сложность алгоритма во время выполнения - это функция, определяемая последовательностью операций, применяемых к вводу размера a и усредняемой по времени.