логика

Алгебра логики (булева алгебра) - это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними.

Джордж Буль

Логическое высказывание — это любое повествовательное предложение, в отношении которого можно однозначно сказать, истинно оно или ложно.

Пример:
«Трава зеленая» -истинное высказывание.
«Лев – птица» - ложное высказывание.

Не всякое предложение является логическим высказыванием.
Пример:
«ученик десятого класса»
«информатика — интересный предмет».

Употребляемые в обычной речи слова и словосочетания "не", "и", "или", "если... , то", "тогда и только тогда" и другие позволяют из уже заданных высказываний строить новые высказывания.
Такие слова и словосочетания называются логическими связками.

Высказывания, образованные из других высказываний с помощью логических связок, называются составными.
Высказывания, не являющиеся составными, называются элементарными.

Пример:
Элементарные высказывания:
«Петров — врач»,
«Петров — шахматист»
Составные высказывания:
"Петров — врач и шахматист", понимаемое как "Петров — врач, хорошо играющий в шахматы".
"Петров — врач или шахматист", понимаемое в алгебре логики как "Петров или врач, или шахматист, или и врач и шахматист одновременно".

Чтобы обращаться к логическим высказываниям, их обозначают буквами.
Пример:
А = «Луна – спутник Земли», А = 1
В = « 3* 2 = 5», В = 0

Пример:
А ="Тимур поедет летом на море",
В = "Тимур летом отправится в горы".
А и В = "Тимур летом побывает и на море, и в горах»

Операции над логическими
высказываниями

Таблица истинности это табличное представление логической схемы (операции), в котором перечислены все возможные сочетания значений истинности входных сигналов (операндов) вместе со значением истинности выходного сигнала (результата операции) для каждого из этих сочетаний.

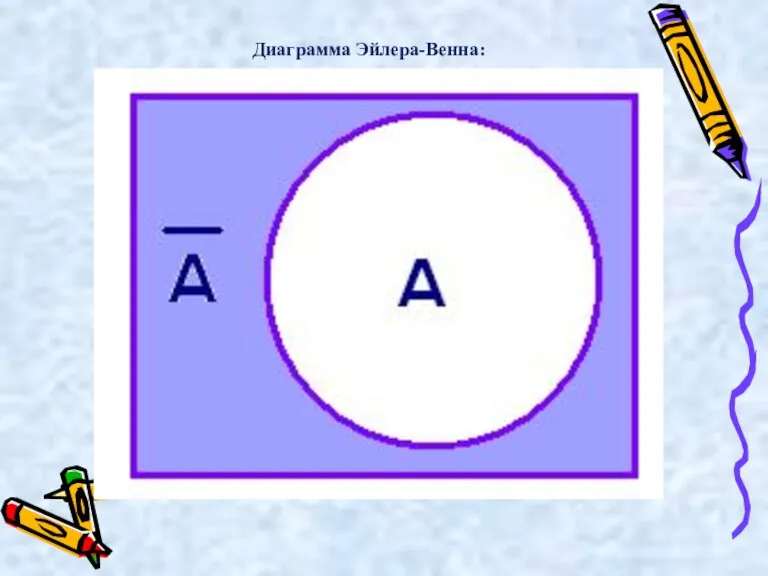
Логическое «отрицание»
(инверсия или НЕ) обозначается чертой над высказыванием Ā .

Диаграмма Эйлера-Венна:

Пример:
А = «Луна — спутник Земли»
А = "Луна — не спутник Земли"

Высказывание А истинно, когда A ложно, и ложно, когда A истинно.
Таблица истинности

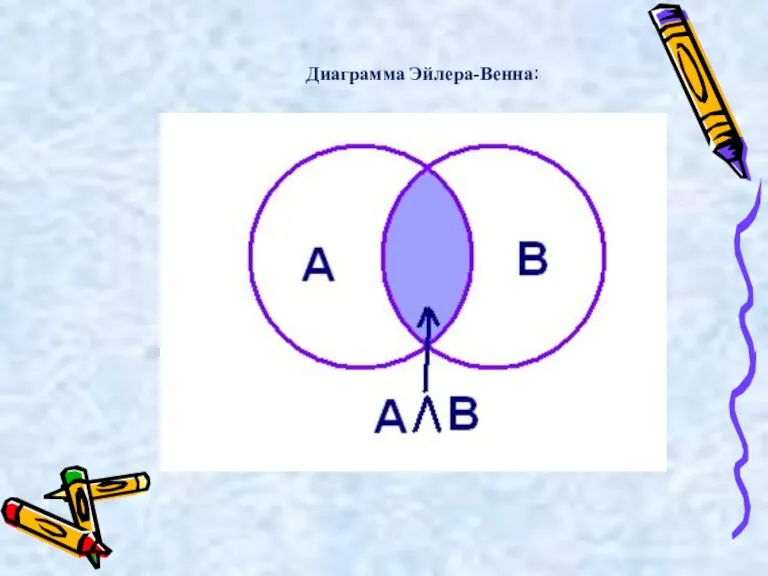
Логическое умножение
( «и», конъюнкция (лат. conjunctio — соединение)) обозначается точкой " . " (может также обозначаться знаками /\ или &).
А . В, А /\ В, А & В

Диаграмма Эйлера-Венна:

Пример:
А = «10 делится на 2», А= 1
В = «5 больше 3», В = 1
С = « 4 – нечётное число», С = 0
А & В = «10 делится на 2 и 5 больше 3», А & В = 1
А & С = «10 делится на 2 и 4 – нечётное число», А & С = 0

Высказывание А · В истинно тогда и только тогда, когда оба высказывания А и В истинны.
Таблица истинности

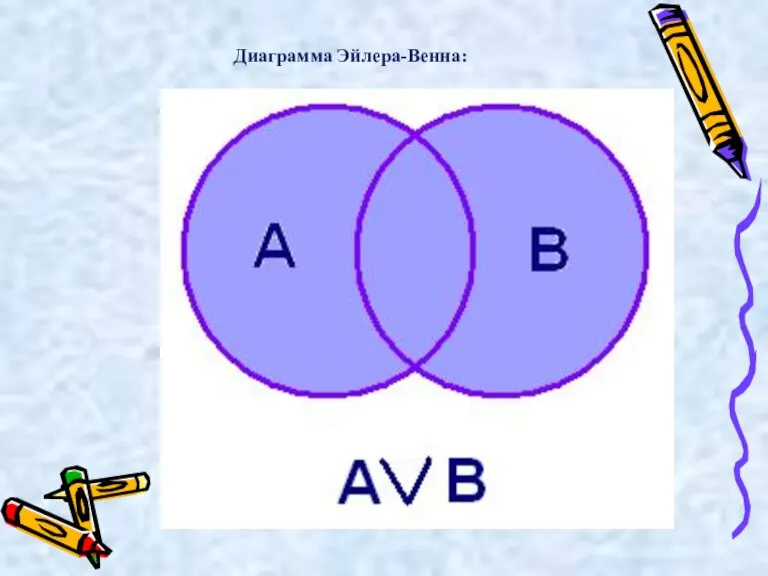
Логическое сложение
( «или», дизъюнкция (лат. disjunctio — разделение) обозначается знаком v или +.
А V В, А + В

Диаграмма Эйлера-Венна:

Высказывание А v В ложно тогда и только тогда, когда оба высказывания А и В ложны.
Таблица истинности

Импликация (лат. implico — тесно связаны)
-операция, выражаемая связками «если ..., то…», «из ... следует…», «... влечет ...».
Обозначается знаком .
А В
.

Высказывание А В ложно тогда и только тогда, когда А истинно, а В – ложно.
Таблица истинности

Эквиваленция (двойная импликация)
- операция, выражаемая связками «тогда и только тогда», «необходимо и достаточно», «... равносильно ...» Обозначается знаком или ~.
А В, А ~ В.

Высказывание А В истинно тогда и только тогда, когда значения А и В совпадают.
Таблица истинности

А = «10 делится на 2», А= 1
В = «5 больше 3», В = 1
С = « 4 – нечётное число», С = 0
К = « 3 – чётное число», К = 0
А + В = «10 делится на 2 или 5 больше 3», А + В = 1
А + С = «10 делится на 2 или 4 – нечётное число», А + С = 1
С + К = « 4 – нечётное число или 3 – чётное число», С+К = 0
Пример:

Порядок выполнения логических операций
1.Сначала выполняется операция отрицания (“не”),
2. Затем конъюнкция (“и”),
3. После конъюнкции — дизъюнкция (“или”),
4. В последнюю очередь — импликация и эквиваленция.

A → B = ¬ A ∨ B
Законы де Моргана ¬ (A ∧ B) = ¬ A ∨ ¬ B
¬ (A ∨ B) = ¬ A ∧ ¬ B
3. Законы коммутативности А&B ⬄ B&A
AVB ⬄ BVA
4. Законы ассоциативности (А&B)&C ⬄ A&(B&C)
(АVB)VC ⬄ AV(BVC)
5. Законы дистрибутивности А&(BVC) ⬄ (A&B)V(A&C)
АV(B&C) ⬄ (AVB)&(AVC)
6. Законы поглощения A&(AVB)⬄A
AV(A&B)⬄A
7. Законы противоречия A&¬A=0
8. Закон исключения третьего AV¬A=1
9. Закон двойного отрицания ¬¬A=A
10. Закон контрапозиции A-›B⬄ ¬A->¬B
Законы логики.