Слайд 2Понятие кортежа
Понятие кортежа, как и понятие множества, является одним из основных математических

понятий, поэтому для него также не существует определения через другие понятия. Интуитивно кортеж можно определить как упорядоченный набор компонентов. Кортежи одинаковы (равны), если они состоят из одних и тех же компонентов, причем порядок этих компонентов также одинаков.
Слайд 3Компоненты кортежей обычно перечисляются в круглых скобках.
Например, a = (3, 8, 2)

– кортеж. Числа 3, 8, 2 – его компоненты.
Другой пример кортежа – c = (8, 2, 3). Кортежи a и c – разные.
В кортеже могут быть одинаковые элементы. Например, x = (8, 3, 2, 3) и y = (3, 8, 2, 3) – кортежи, причем разные.
Слайд 4Количество компонентов в кортеже называется его длиной. Например, длина кортежей a и

c равна трем, а кортежей x и y – четырем. Кортежи из двух компонентов называют парами, из трех – тройками, и т.д.
Простейший пример кортежа – вектор, задающий координаты точки на плоскости или в пространстве. Очевидно, что, например, точки на плоскости с координатами (5, 7) и (7, 5) – разные.
Как и для множеств, компоненты кортежей могут быть любыми (не только числами). Например, перечень студентов учебной группы, упорядоченный по их среднему баллу за время учебы, можно считать кортежем.
Слайд 5История возникновения теории графов
Родоначальником теории графов считается Леонард Эйлер. В 1736 году

в одном из своих писем он формулирует и предлагает решение задачи о семи кёнигсбергских мостах, ставшей впоследствии одной из классических задач теории графов. Термин «граф» впервые ввел Сильвестр, Джеймс Джозеф в 1878 году в своей статье в Nature.
Слайд 6Понятие графа
В математике, Граф — это абстрактное представление множества объектов и связей

между ними. Графом называют пару (V, E) где V это множество вершин, а E множество пар, каждая из которых представляет собой связь (эти пары называют рёбрами).
Слайд 7Граф может быть ориентированным или неориентированным. В ориентированном графе, связи являются направленными

(то есть пары в E являются упорядоченными, например, пары (a, b) и (b, a) это две разные связи). В свою очередь в неориентированном графе, связи ненаправленные, и поэтому если существует связь (a, b) то значит, что существует связь (b, a).
Слайд 8Степень
Степень вершины может быть входящая и исходящая (для неориентированных графов входящая степень

равна исходящей).
Входящая степень вершины v это количество ребер вида (i, v), то есть количество ребер которые «входят» в v.
Исходящая степень вершины v это количество ребер вида (v , i), то есть количество ребер которые «выходят» из v.
Это не совсем формальное определение (более формально определение через инцидентность), но оно вполне отражает суть
Слайд 9Путь
Путь в графе это конечная последовательность вершин, в которой каждые две вершины идущие подряд соединены ребром. Путь

может быть ориентированным или неориентированным в зависимости от графа.
У графов есть ещё много разных свойств (например они могут быть связными, двудольными, полными), но я не буду описывать все эти свойства сейчас, а в следующих частях когда эти понятия понадобятся нам.
Слайд 10Пусть даны множества X1,X2,...,Xn. Кортежем длины n, составленным из элементов этих множеств,

называется конечная последовательность α=(x1,x2,..,xk), где для всех k, 1≤k≤n, xk∈Xk.
Элемент xk называется k-й координатой или k-й компонентой кортежа α.
Два кортежа равны в том и только том случае, когда они имеют одинаковую длину и их соответствующие координаты равны, т.е. кортежи α=(x1,...,xm) и β=(y1,...,yn) равны только в том случае, когда m=n и xk=yk для всех 1≤k≤n.
Слайд 11Кортежи длины
Кортежи длины два называются упорядоченными парами, длины три — упорядоченными тройками,

длины n — упорядоченными n-ками. Для краткости слово “упорядоченные” обычно опускают.
Кортеж, не содержащий ни одной координаты, имеет длину 0 и называется пустым.
Слайд 12Пусть даны множества A,B. Прямым (декартовым) произведением множеств A и B называется

множество, состоящее из пар (a,b), где a∈A и b∈B, обозначается A×B.
n-й декартовой степенью множества A называется его прямое n-кратное произведение на самого себя, обозначается: An.
An=A×An−1
Слайд 13Многие математические объекты формально определяются как кортежи.
Например, ориентированный граф определяется как

пара (V,E) где V — это множество вершин, а E — подмножество пар в V×V, соответствующих дугам графа. Точка в n-мерном пространстве действительных чисел определяется как кортеж длины n, составленный из элементов множества действительных чисел.
Во многих задачах, особенно, решаемых на ЭВМ, графы удобно описывать матрицами.
Слайд 141.Задание графов матрицей смежности:
Матрица смежности – это квадратная матрица порядка p (количество

вершин), элемент которой, стоящий в i строке и j столбце определяется по правилу:
Слайд 152. Задание графов матрицей инцидентций
Матрицей инцидентции называется прямоугольная матрица размерности (p –

количество вершин, q – количество ребер), элемент которой стоящий в i строке и j столбце определяется по правилу:
- для неориентированного графа.















 Библиотека Кировских островов
Библиотека Кировских островов Итераторы и функциональные объекты
Итераторы и функциональные объекты Основы программирования (на языке Си). Массивы
Основы программирования (на языке Си). Массивы Проект Витрина
Проект Витрина Шаблоны писем
Шаблоны писем Профессия гейм-дизайнер
Профессия гейм-дизайнер Урок - игра Основы информатики
Урок - игра Основы информатики Мировой класс лидирующих компаний в цифровой струйной печати
Мировой класс лидирующих компаний в цифровой струйной печати Архитектура современной ЭВМ. Состав и характеристики комплектующих современного персонального компьютера
Архитектура современной ЭВМ. Состав и характеристики комплектующих современного персонального компьютера Skype-конференция
Skype-конференция 3. Выбор жизненного цикла ИТ-проекта.Использование гибких подходов в управлении ИТ-проектами
3. Выбор жизненного цикла ИТ-проекта.Использование гибких подходов в управлении ИТ-проектами Примеры использования внешних устройств. Программное обеспечение внешних устройств
Примеры использования внешних устройств. Программное обеспечение внешних устройств Создание комплексной системы обеспечения информационной безопасности инфраструктуры Росреестра
Создание комплексной системы обеспечения информационной безопасности инфраструктуры Росреестра Хранители Равновесия
Хранители Равновесия База данных
База данных Технические новинки первой мировой войны
Технические новинки первой мировой войны Структуры данных: стеки, деки, очереди
Структуры данных: стеки, деки, очереди Интерактивная доска (ИД)
Интерактивная доска (ИД) Презентация на тему Примеры моделирования
Презентация на тему Примеры моделирования  Информационные технологии. Тема № 3. Основы защиты информации
Информационные технологии. Тема № 3. Основы защиты информации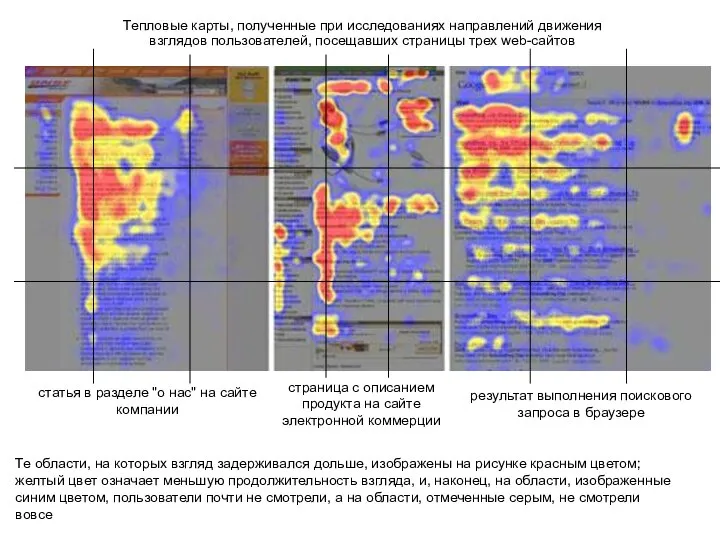 Тепловые карты, полученные при исследованиях направлений движения взглядов пользователей, посещавших страницы трех web-сайтов
Тепловые карты, полученные при исследованиях направлений движения взглядов пользователей, посещавших страницы трех web-сайтов Функциональное программное обеспечение решения управленческих задач
Функциональное программное обеспечение решения управленческих задач Дизайн и графика. Web-страницы
Дизайн и графика. Web-страницы Источники пространственных данных. Их типы. Способы получения данных
Источники пространственных данных. Их типы. Способы получения данных Организация сетевого администрирования
Организация сетевого администрирования 3
3 One Drive
One Drive Создание групп (сообществ) в образовательной сети
Создание групп (сообществ) в образовательной сети