Содержание
- 2. Джордж Буль 1815 -1864 «Имеется глубокая аналогия между символическим методом алгебры и символическим методом представления логических
- 3. Алгебра высказываний (Алгебра логики, Булева алгебра) Высказывания представляются логическими переменными, которые могут иметь всего два значения:
- 4. Простые высказывания Волга впадает в Каспийское море a=1 Амур впадает в Каспийское море a=0 Возможно осложнение
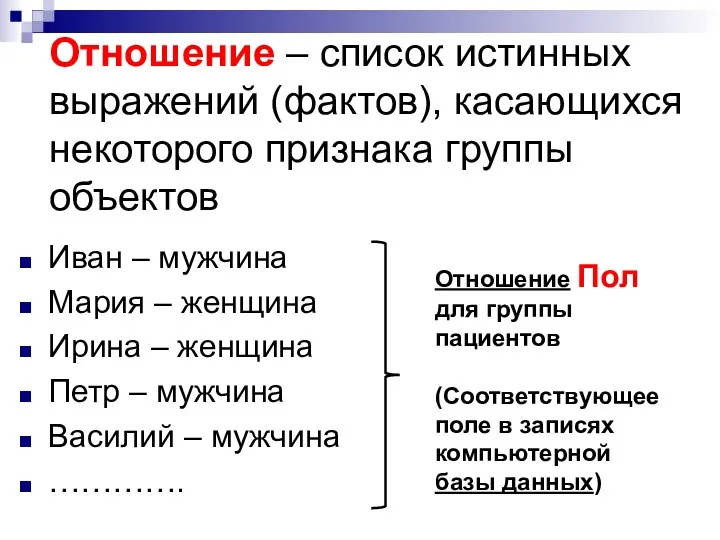
- 5. Отношение – список истинных выражений (фактов), касающихся некоторого признака группы объектов Иван – мужчина Мария –
- 6. Предикат – логическая функция, определенная над отношением Предикат имеет значение Истина, если его аргумент принадлежит отношению,
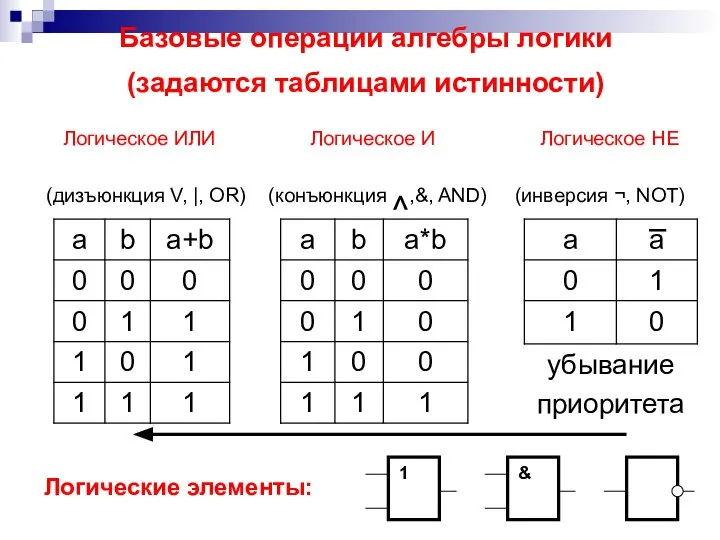
- 7. Базовые операции алгебры логики (задаются таблицами истинности) Логическое ИЛИ Логическое И Логическое НЕ (дизъюнкция V, |,
- 8. Операции с константами: a + 0 = a a + 1 = 1 a * 0
- 9. Сын: можно мне пойти в кино или купить мороженое? Мама: нет Нельзя пойти в кино и
- 10. Порядок выполнения операций можно изменять с помощью скобок: Переместительный закон: a + b = b +
- 11. Любая сколь угодно сложная логическая функция, заданная своей таблицей истинности, может быть представлена логическим выражением в
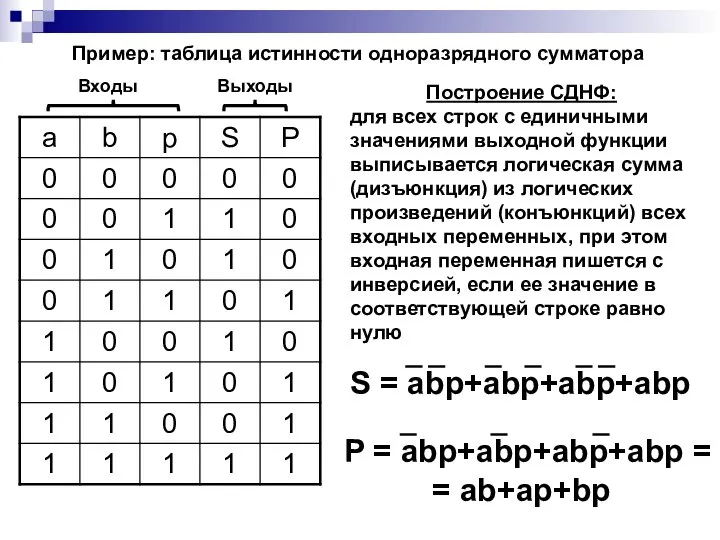
- 12. S = abp+abp+abp+abp P = abp+abp+abp+abp = = ab+ap+bp Пример: таблица истинности одноразрядного сумматора Построение СДНФ:
- 13. Логическая операция «Импликация»: а -> b a – Посылка b – Следствие Если a, то b
- 14. Импликация над предикатами называется продукционным правилом Пример: Если ( x – мужчина ) И ( x
- 15. Тестовые задания по теме лекции
- 16. Результат логической операции ДИЗЪЮНКЦИЯ (логическое ИЛИ) от двух переменных равен ИСТИНА, если |1. Значение хотя бы
- 17. Результат логической операции КОНЪЮНКЦИЯ (логическое И) от двух переменных равен ИСТИНА, если |1. Значение хотя бы
- 18. Результат логической операции ДИЗЪЮНКЦИЯ с ИНВЕРСИЕЙ (логическое ИЛИ-НЕ) от двух переменных равен ИСТИНА, если |1. Значение
- 19. Результат логической операции КОНЪЮНКЦИЯ с ИНВЕРСИЕЙ (логическое И-НЕ) от двух переменных равен ИСТИНА, если |1. Значение
- 20. В результате поиска в базе данных пациентов по условию ВОЗРАСТ больше 30 лет И ВОЗРАСТ меньше
- 21. В результате поиска в базе данных пациентов по условию ВОЗРАСТ больше 30 лет ИЛИ ВОЗРАСТ меньше
- 22. В приведенных ниже логических равенствах (знак дизъюнкции +, знак конъюнкции *) неверным является |1. a +
- 23. Тестовые задания с единого портала интернет-тестирования в сфере образования
- 24. Правильный ответ 3
- 25. Правильный ответ 1
- 26. По формуле де Моргана для выражения в скобках правильный ответ 4
- 27. Правильный ответ 3
- 29. Скачать презентацию























 Гиперссылки на Web-страницах
Гиперссылки на Web-страницах Кибер-безопасность
Кибер-безопасность Представление количественных результатов в журнальных публикациях
Представление количественных результатов в журнальных публикациях Программное обеспечение учетных и статистических операций
Программное обеспечение учетных и статистических операций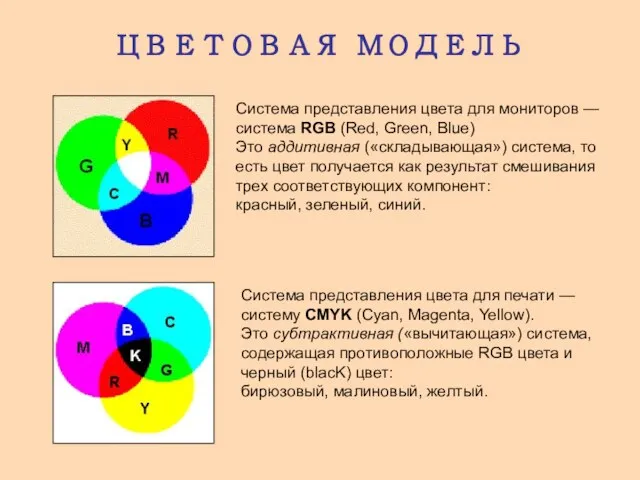 Цветовая модель
Цветовая модель Триггеры. Применение
Триггеры. Применение I часть бланка, выданного экспериментатором
I часть бланка, выданного экспериментатором СУБД ACCESS. Создание таблиц, запросов. (Лекция 4-2)
СУБД ACCESS. Создание таблиц, запросов. (Лекция 4-2) Кабели и контакты
Кабели и контакты Мировой опыт: indoor-медианосители, которые можно адаптировать в РФ
Мировой опыт: indoor-медианосители, которые можно адаптировать в РФ Система электронных ценников на базе Е-INK технологии
Система электронных ценников на базе Е-INK технологии Отдел программирования и автоматизации
Отдел программирования и автоматизации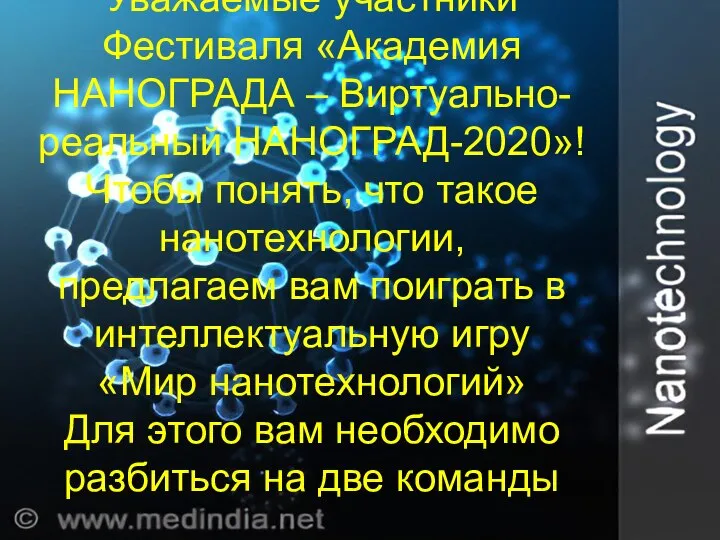 Мир нанотехнологий. Игра
Мир нанотехнологий. Игра 1с: бухгалтерия
1с: бухгалтерия Техника безопасности в компьютерном классе. Игра
Техника безопасности в компьютерном классе. Игра IoC Inversion of Control инверсия управления. Dependency Injection (внедрение зависимостей)
IoC Inversion of Control инверсия управления. Dependency Injection (внедрение зависимостей) Планета алгоритмика. Клад
Планета алгоритмика. Клад Friend Systems. Заработок в интернете
Friend Systems. Заработок в интернете Краткая характеристика изученных программ
Краткая характеристика изученных программ Элементы алгебры логики математические основы информатики
Элементы алгебры логики математические основы информатики Медиапотрбеление
Медиапотрбеление Измерительные шкалы. Расплывчатое и вероятностное описание ситуаций
Измерительные шкалы. Расплывчатое и вероятностное описание ситуаций Конструкторы бизнес-приложений баз данных
Конструкторы бизнес-приложений баз данных Понятие CMS, возможности 1С-Битрикс
Понятие CMS, возможности 1С-Битрикс Типология средств массовой информации
Типология средств массовой информации HTML - второй урок
HTML - второй урок Типы данных
Типы данных Меdиа школа
Меdиа школа