1. Париж - столица Англии.
2. Санкт-Петербург – город на Неве. 2. Карась не рыба.
3. Июнь – шестой месяц года. 3. Корова - плотоядное животное.
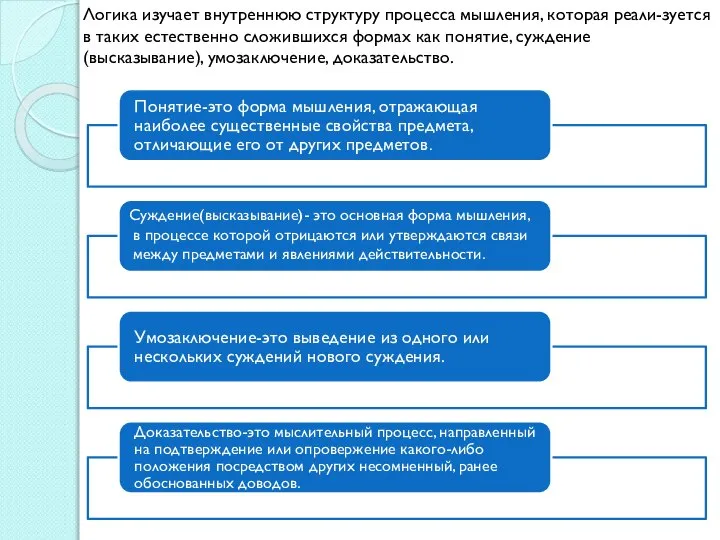
Также высказывания бывают простыми и сложными.
Простым (элементарным) называется высказывание, никакая часть которого сама не является высказывание.
Соединяя простые высказывания связками «и», «или», «если..., то...», «не», «тогда», «следует», «но», «а», «равносильно», «эквивалентно» и др. можно строить новые высказывания, которые называются составными.
Составное логическое высказывание —это высказывание,
образованное из других высказываний с помощью логических связок.
Высказывания бывают истинными и ложными(истина – 1, ложь - 0).
ВЫСКАЗЫВАНИЯ









 Квалификационные требования к подготовке презентаций
Квалификационные требования к подготовке презентаций Машинки. Прямо
Машинки. Прямо Модуль Мероприятия
Модуль Мероприятия Устройство компьютера. Тема 1. Основные устройства компьютера. Системный блок: Процессор. Память
Устройство компьютера. Тема 1. Основные устройства компьютера. Системный блок: Процессор. Память Состав вычислительной системы (лекция 1)
Состав вычислительной системы (лекция 1) Презентация на тему Компьютер – универсальное устройство обработки информации
Презентация на тему Компьютер – универсальное устройство обработки информации  Компонент FORM (3)
Компонент FORM (3) Защита операционной системы при работе в интернете с помощью модема-маршрутизатора
Защита операционной системы при работе в интернете с помощью модема-маршрутизатора Ein kurzer Diskurs zu OM5 und ihre Vor- und Nachteile für Rechenzentrumbetreiber!
Ein kurzer Diskurs zu OM5 und ihre Vor- und Nachteile für Rechenzentrumbetreiber! Изменение размера и шрифта текста в документе Microsoft Word. Урок 4
Изменение размера и шрифта текста в документе Microsoft Word. Урок 4 Информатика для 4 класса. Компьютерные программы
Информатика для 4 класса. Компьютерные программы Общие сведения о персональном компьютере
Общие сведения о персональном компьютере Перевод при помощи NeoDic
Перевод при помощи NeoDic Открытый урок информатики с применением сингапурских методов (структур)
Открытый урок информатики с применением сингапурских методов (структур)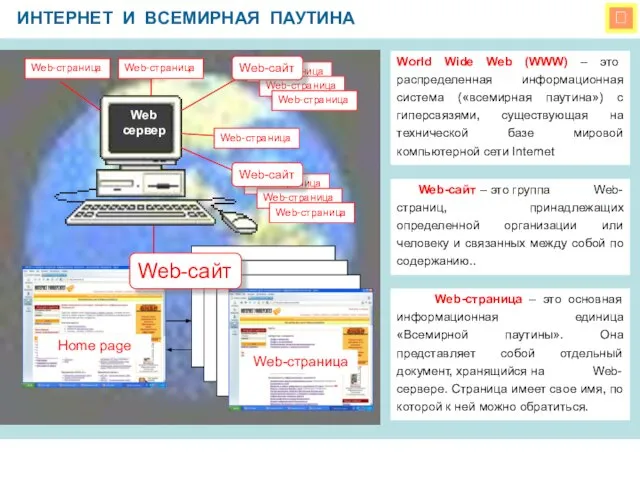 Интернет и всемирная паутина
Интернет и всемирная паутина Оформление заявления на получение водительского удостоверения
Оформление заявления на получение водительского удостоверения Презентация
Презентация Исполнитель Робот
Исполнитель Робот Программные комплексы поддержки принятия управленческих решений (на примере ООО Центр-Сервис)
Программные комплексы поддержки принятия управленческих решений (на примере ООО Центр-Сервис) Microsoft Office. Основные компоненты
Microsoft Office. Основные компоненты Особенности проведения ГИА-11, ГИА-9
Особенности проведения ГИА-11, ГИА-9 Машинное обучение на языке программирования Python
Машинное обучение на языке программирования Python Программирование на языке Паскаль. Циклы с условием
Программирование на языке Паскаль. Циклы с условием Как найти научную информацию?
Как найти научную информацию? Темы выступлений группы учеников: Атмосфера Земли. Понятие мультимедиа
Темы выступлений группы учеников: Атмосфера Земли. Понятие мультимедиа Циклический алгоритм
Циклический алгоритм Объектно-ориентированное программирование. Часть 2
Объектно-ориентированное программирование. Часть 2 Основные проблемы в написании С2.1 и пути их решения
Основные проблемы в написании С2.1 и пути их решения