Содержание
- 2. Математическая логика § 5. Логика и компьютер
- 3. Логика, высказывания Логика (др.греч. λογικος) – это наука о том, как правильно рассуждать, делать выводы, доказывать
- 4. Высказывание или нет? Сейчас идет дождь. Жирафы летят на север. История – интересный предмет. У квадрата
- 5. Логика и компьютер Логика изучает операции между 0 и 1! Джордж Буль Алгебра логики — это
- 6. Простые и составные высказывания A – Сейчас идет дождь. B – Форточка открыта. простые высказывания (элементарные)
- 7. Операция НЕ (инверсия) Если высказывание A истинно, то «не А» ложно, и наоборот. 1 0 0
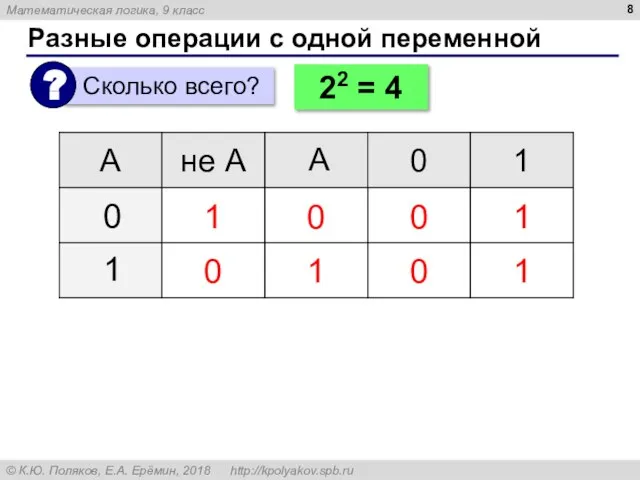
- 8. Разные операции с одной переменной 1 0 0 1 1 0 А 0 0 1 1
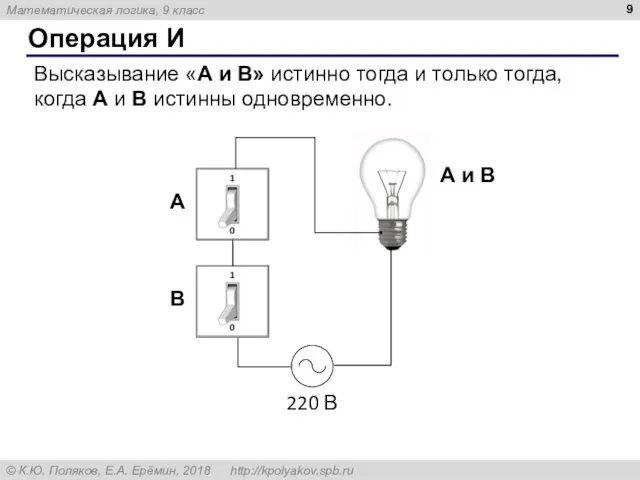
- 9. Операция И Высказывание «A и B» истинно тогда и только тогда, когда А и B истинны
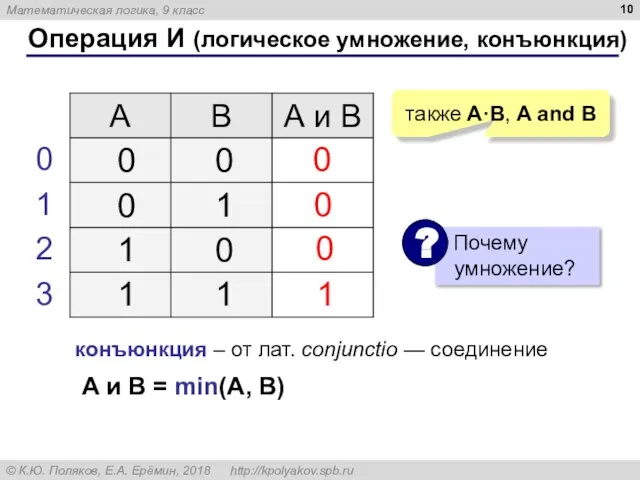
- 10. Операция И (логическое умножение, конъюнкция) 1 0 также A·B, A and B 0 0 конъюнкция –
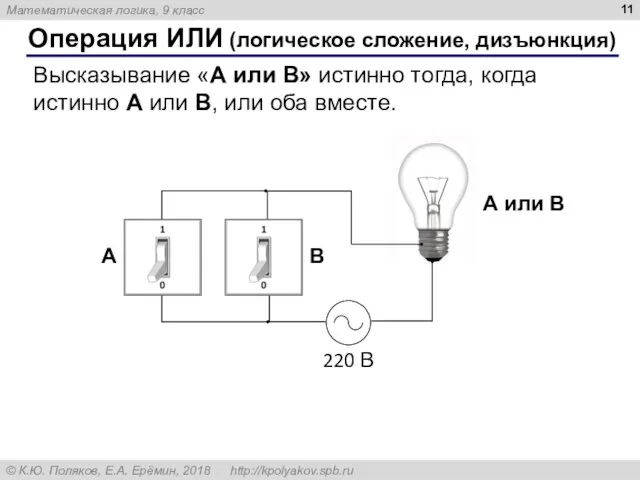
- 11. Операция ИЛИ (логическое сложение, дизъюнкция) Высказывание «A или B» истинно тогда, когда истинно А или B,
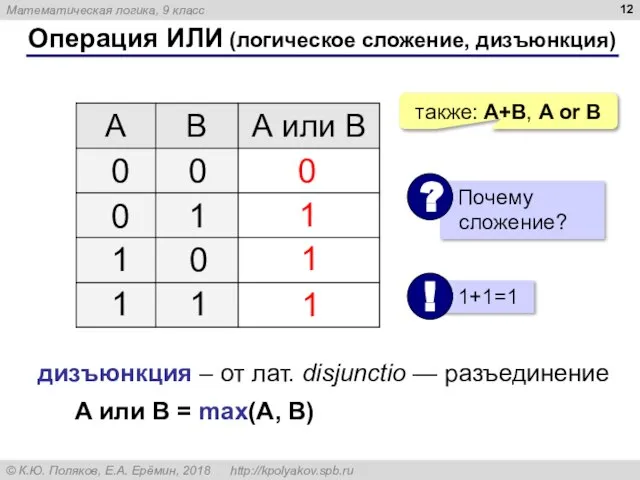
- 12. Операция ИЛИ (логическое сложение, дизъюнкция) 1 0 также: A+B, A or B 1 1 дизъюнкция –
- 13. Упрощение логических выражений A и 0 = A ∙ 0 = A и 1 = A
- 14. Математическая логика § 6. Логические элементы
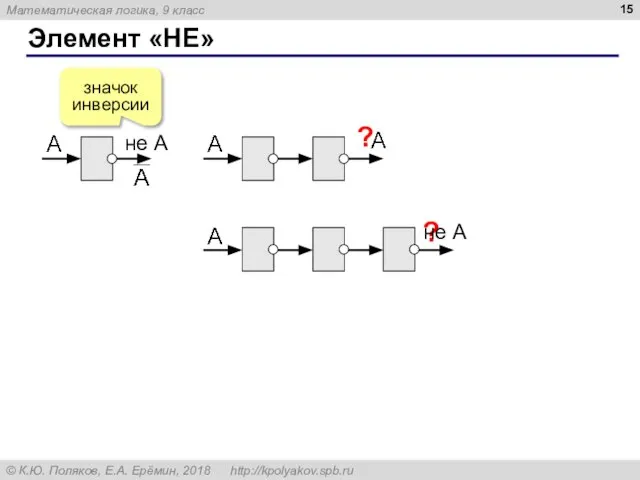
- 15. Элемент «НЕ» значок инверсии ? ? не A не A
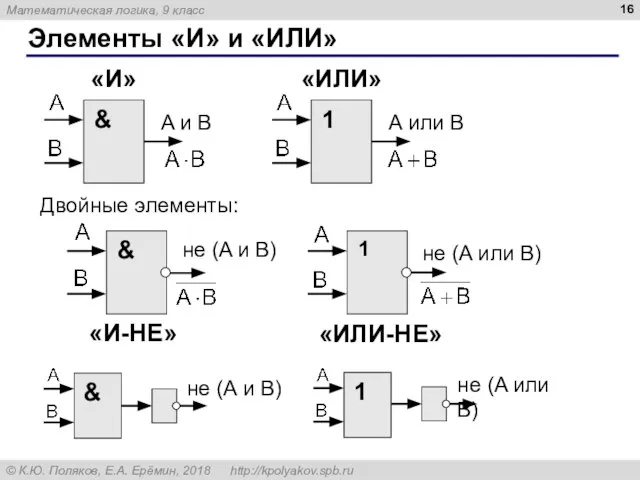
- 16. Элементы «И» и «ИЛИ» A и B A или B Двойные элементы: «ИЛИ-НЕ» «И-НЕ» не (A
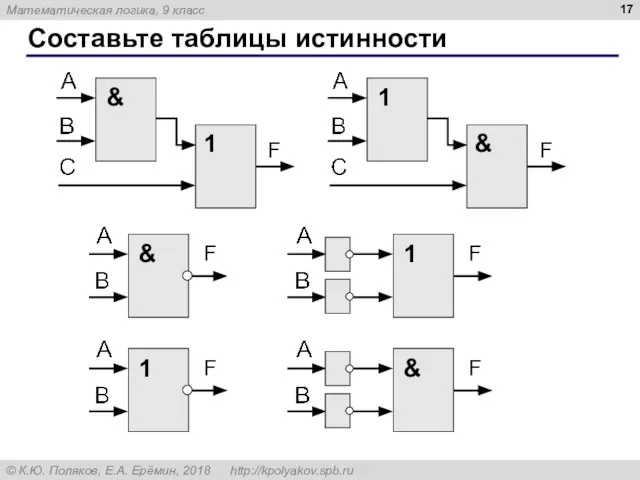
- 17. Составьте таблицы истинности
- 18. Математическая логика § 7. Другие логические операции
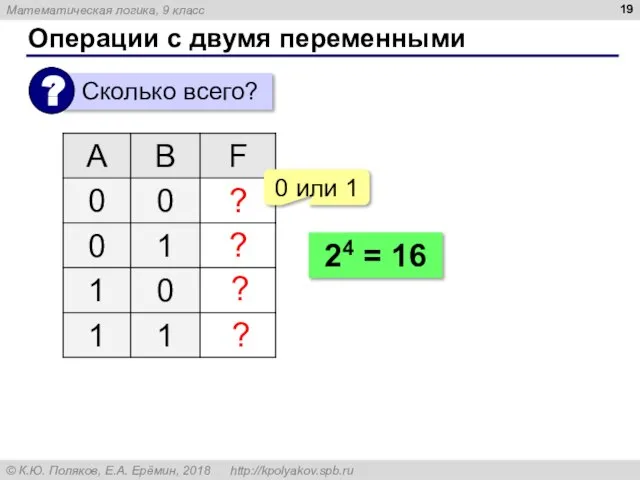
- 19. Операции с двумя переменными ? ? ? ? 0 или 1 24 = 16
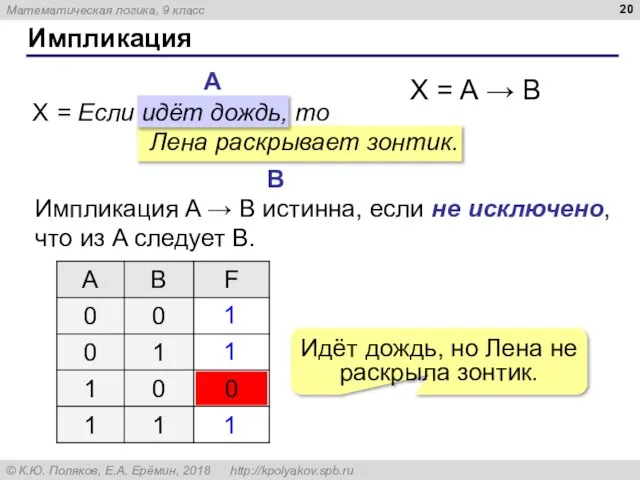
- 20. Импликация X = Если идёт дождь, то Лена раскрывает зонтик. X = A → B Импликация
- 21. Постройте таблицы истинности B → A ≠ A → B X = B → A
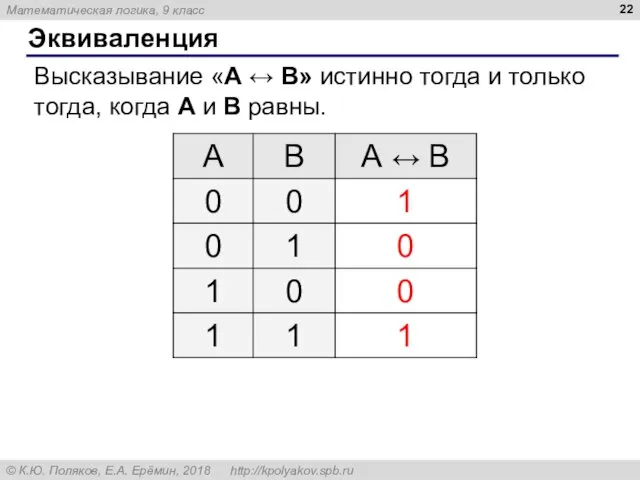
- 22. Эквиваленция Высказывание «A ↔ B» истинно тогда и только тогда, когда А и B равны.
- 23. Постройте таблицы истинности
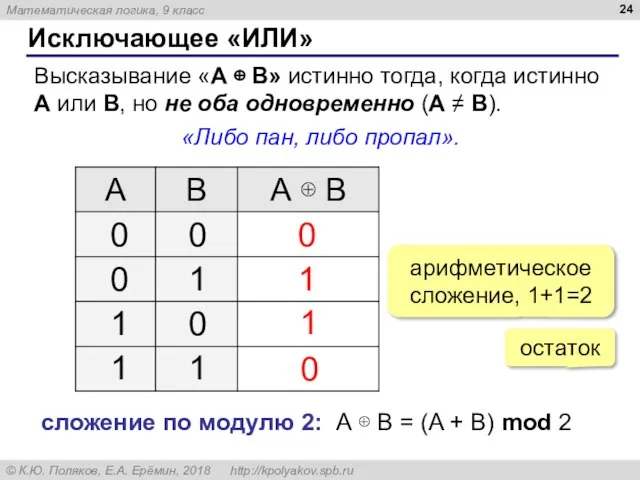
- 24. Исключающее «ИЛИ» Высказывание «A ⊕ B» истинно тогда, когда истинно А или B, но не оба
- 25. Постройте таблицы истинности
- 26. Упрощение логических выражений A ⊕ 0 = A ⊕ 1 = A ⊕ A = (A
- 27. Шифрование (A ⊕ B) ⊕ B = A данные шифровка дешифровка A = 1 0 0
- 28. Математическая логика § 8. Логические выражения
- 29. Логические выражения Логическое выражение — это выражение, результат вычисления которого — логическое значение (истина или ложь).
- 30. Порядок вычисления скобки НЕ И ИЛИ импликация эквиваленция 1 2 3 4 5 6 , исключающее
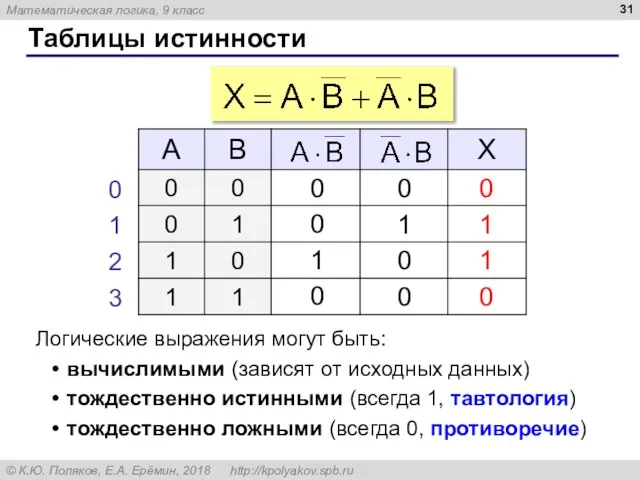
- 31. Таблицы истинности Логические выражения могут быть: вычислимыми (зависят от исходных данных) тождественно истинными (всегда 1, тавтология)
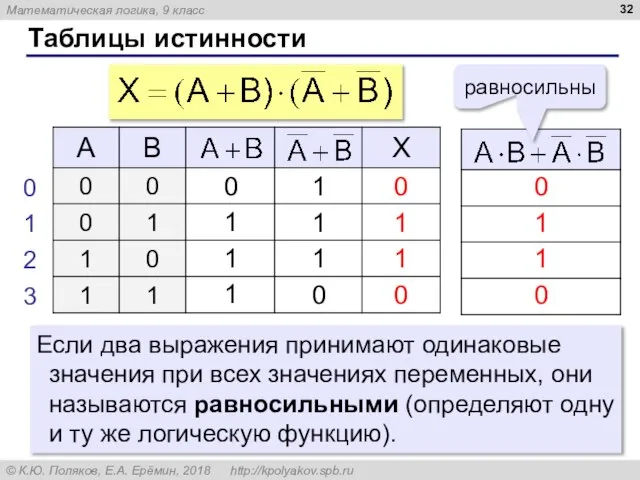
- 32. Таблицы истинности Если два выражения принимают одинаковые значения при всех значениях переменных, они называются равносильными (определяют
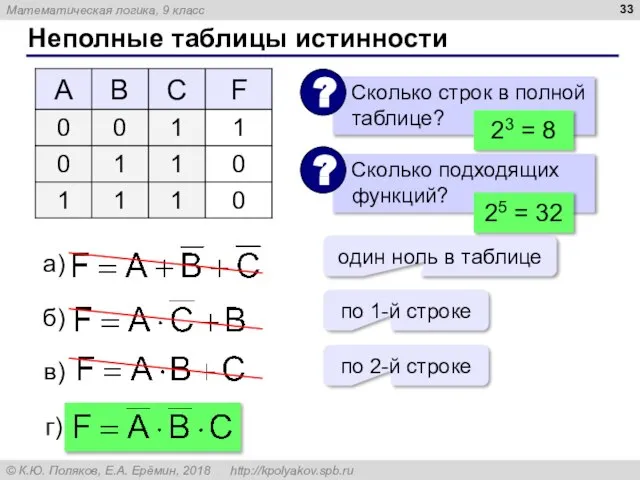
- 33. Неполные таблицы истинности 23 = 8 один ноль в таблице по 1-й строке по 2-й строке
- 34. Сколько нулей и единиц? в таблице истинности функции от 3-х переменных: 1 7 7 1 7
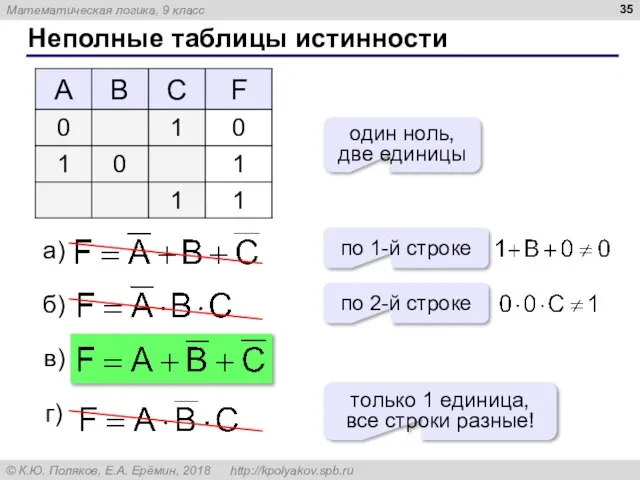
- 35. Неполные таблицы истинности один ноль, две единицы по 1-й строке по 2-й строке только 1 единица,
- 36. Составление условий (x ≥ 3) и (x ≤ 6) (3 ≤ x) и (x ≤ 6)
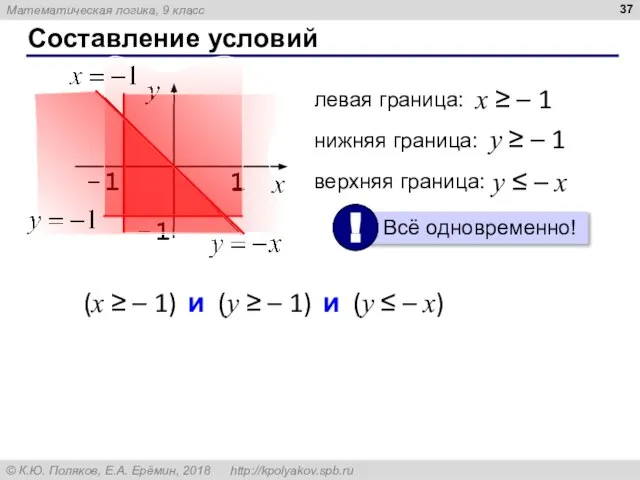
- 37. Составление условий левая граница: x ≥ – 1 нижняя граница: y ≥ – 1 верхняя граница:
- 38. Составление условий (x2+y2 ≤ 1) и (x ≤ 0) левая правая (x ≥ 0) и (x2+y2
- 39. Составление условий = + ((x2+y2 ≤ 1) и (x ≤ 0)) или ((x2+y2 ≤ 1) и
- 40. Определение истинности выражений Для каких из указанных значений числа X истинно высказывание: (X X = 2:
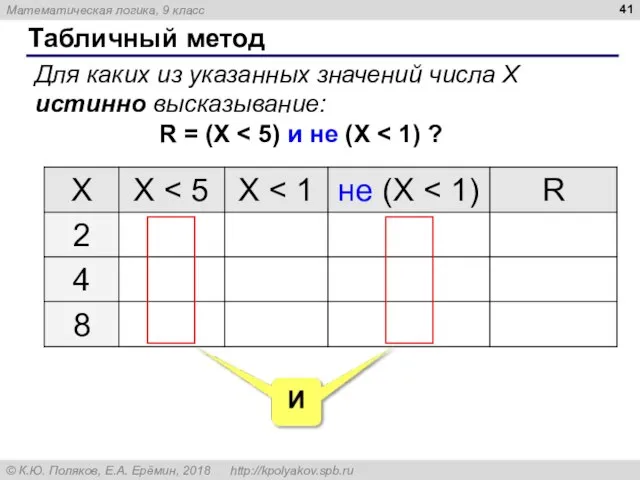
- 41. Табличный метод Для каких из указанных значений числа X истинно высказывание: R = (X
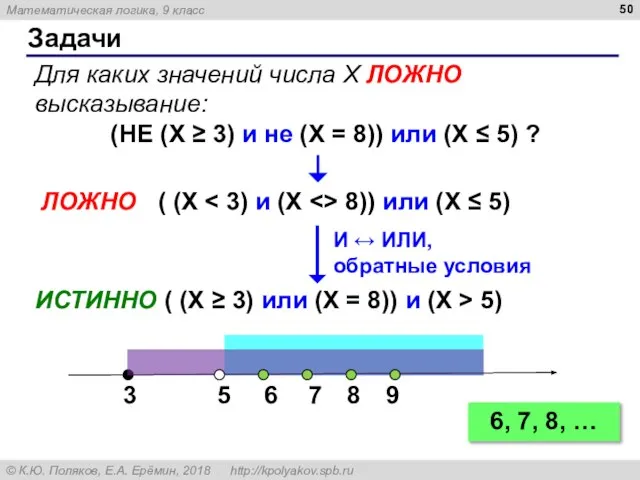
- 42. Задачи Для каких из указанных значений числа X ЛОЖНО высказывание: (не (X ≥ 3) и не
- 43. Задачи Для каких значений числа X истинно высказывание: (X (X = 1) 1, 2, 3, 4
- 44. Задачи Для каких из приведённых имён ЛОЖНО высказывание: НЕ(Первая буква гласная) или (Последняя буква гласная) ?
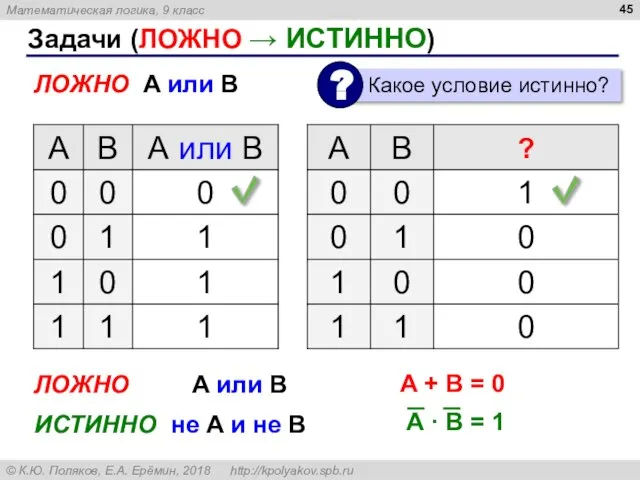
- 45. Задачи (ЛОЖНО → ИСТИННО) ЛОЖНО A или B ЛОЖНО A или B ИСТИННО не A и
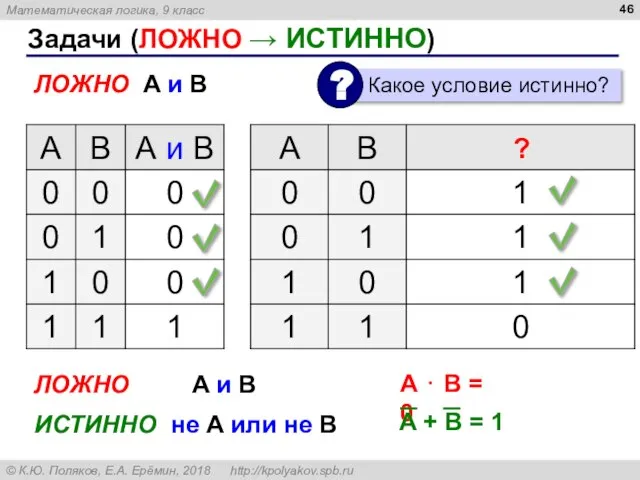
- 46. Задачи (ЛОЖНО → ИСТИННО) ЛОЖНО A и B ЛОЖНО A и B ИСТИННО не A или
- 47. Задачи (ЛОЖНО → ИСТИННО)
- 48. Задачи Для каких из приведённых имён ЛОЖНО высказывание: НЕ(Первая буква гласная) или (Последняя буква гласная) ?
- 49. Задачи Для каких из приведённых имён ЛОЖНО высказывание: НЕ(Первая буква гласная) и (Последняя буква гласная) ?
- 50. Задачи Для каких значений числа X ЛОЖНО высказывание: (НЕ (X ≥ 3) и не (X =
- 51. Задачи Напишите наибольшее число x, для которого истинно высказывание: (x (x 33
- 52. Задачи Напишите наименьшее число x, для которого ЛОЖНО высказывание: (x (x ≥ 42) и (x не
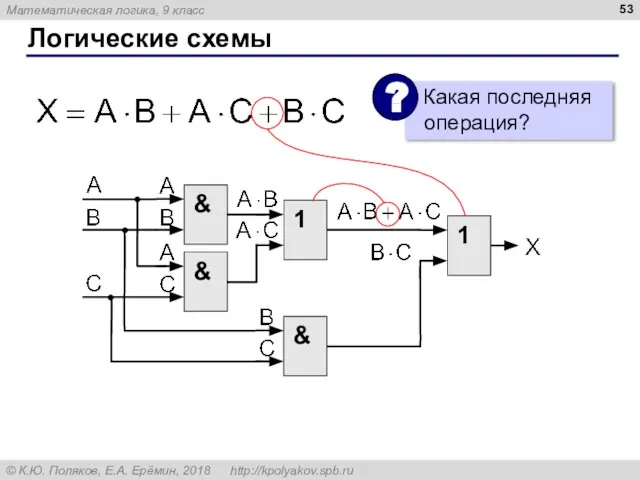
- 53. Логические схемы
- 54. Математическая логика § 12. Множества и логика
- 55. Что такое множество? Множество – некоторый набор элементов, каждый из которых отличается от остальных. пустое множество:
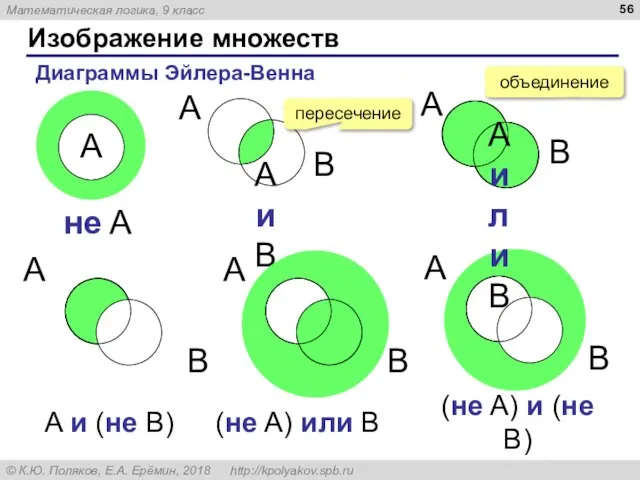
- 56. Изображение множеств Диаграммы Эйлера-Венна A и B A или B (не A) или B пересечение объединение
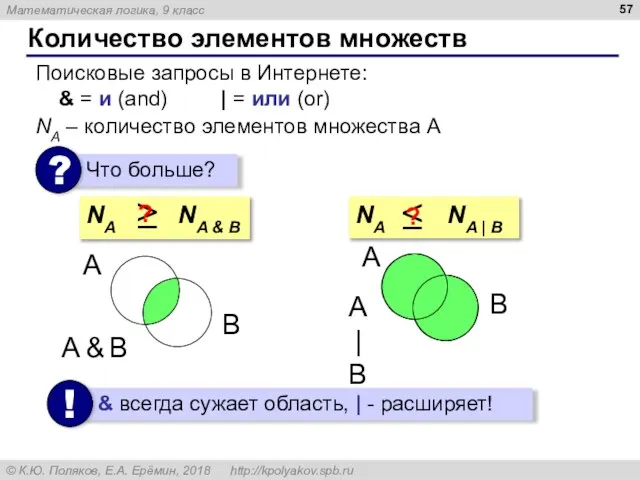
- 57. Количество элементов множеств Поисковые запросы в Интернете: & = и (and) | = или (or) NA
- 58. Задачи В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания количества страниц,
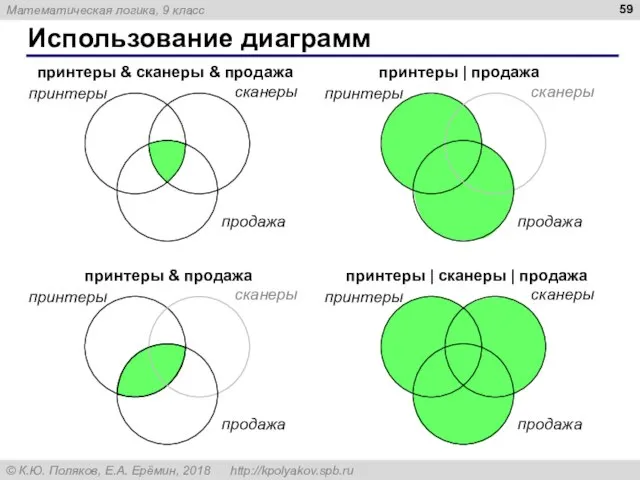
- 59. Использование диаграмм принтеры сканеры продажа принтеры & сканеры & продажа
- 60. Задачи В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке убывания количества страниц,
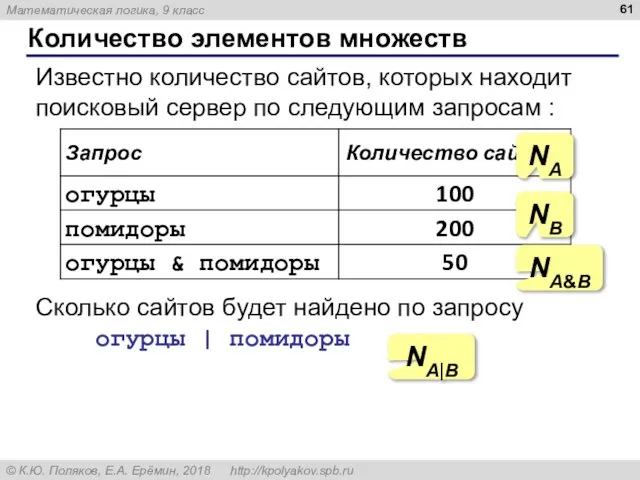
- 61. Количество элементов множеств Известно количество сайтов, которых находит поисковый сервер по следующим запросам : Сколько сайтов
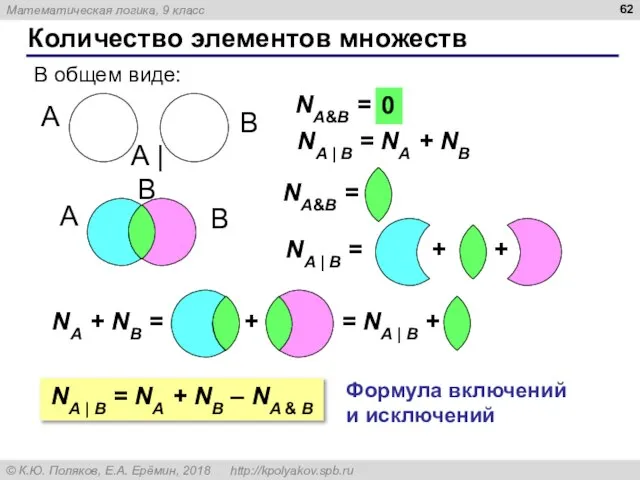
- 62. Количество элементов множеств A B В общем виде: NA&B = ? 0 NA | B =
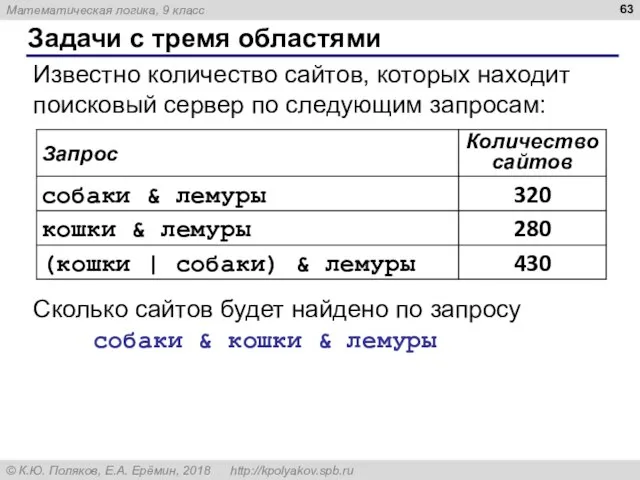
- 63. Задачи с тремя областями Известно количество сайтов, которых находит поисковый сервер по следующим запросам: Сколько сайтов
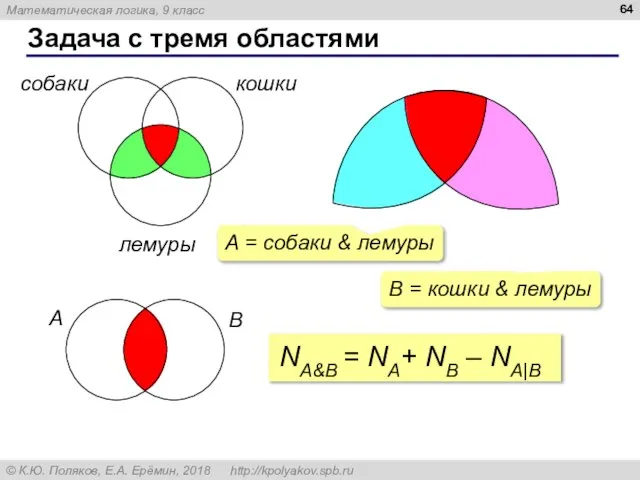
- 64. Задача с тремя областями собаки кошки лемуры B = кошки & лемуры A B NA&B =
- 65. Задачи с тремя областями Известно количество сайтов, которых находит поисковый сервер по следующим запросам: Сколько сайтов
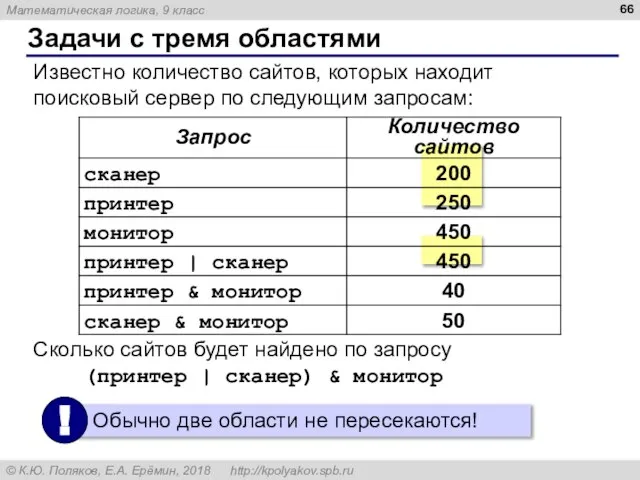
- 66. Известно количество сайтов, которых находит поисковый сервер по следующим запросам: Сколько сайтов будет найдено по запросу
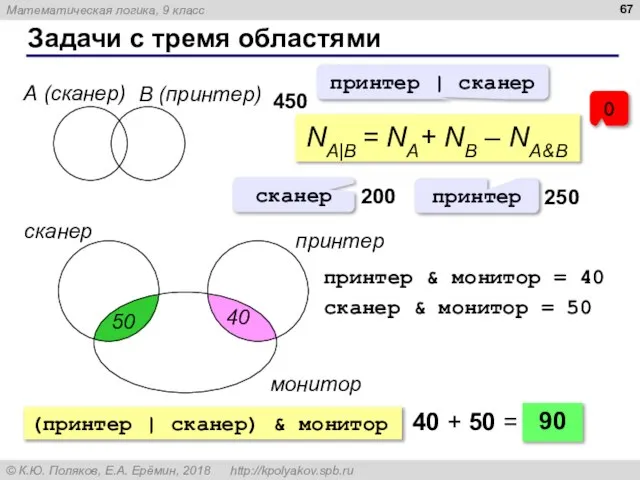
- 67. Задачи с тремя областями А (сканер) B (принтер) NA|B = NA+ NB – NA&B принтер |
- 68. Конец фильма ПОЛЯКОВ Константин Юрьевич д.т.н., учитель информатики ГБОУ СОШ № 163, г. Санкт-Петербург [email protected] ЕРЕМИН
- 70. Скачать презентацию




































 Применение формул для вычисления в таблицах, созданных в Microsoft Word 2007
Применение формул для вычисления в таблицах, созданных в Microsoft Word 2007 Библиотека Кировских островов
Библиотека Кировских островов Библиотека и молодёжь
Библиотека и молодёжь Превращаем фотографию в акварельный рисунок-силуэт
Превращаем фотографию в акварельный рисунок-силуэт Salonoboev.com Онлайн магазин обоев и интерьерных тканей
Salonoboev.com Онлайн магазин обоев и интерьерных тканей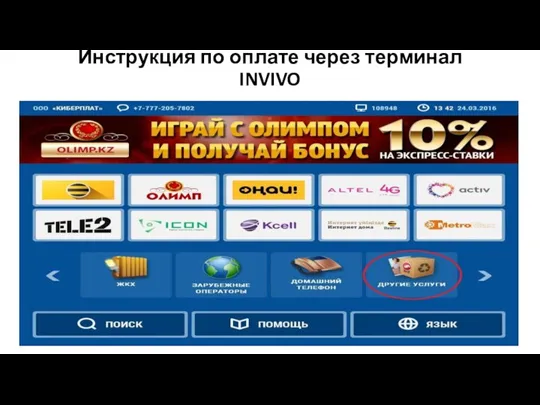 Инструкция по оплате через терминал INVIVO
Инструкция по оплате через терминал INVIVO IP-адресация
IP-адресация Разработка игры DogeClicker
Разработка игры DogeClicker Инструмент для поиска отзывов пользователей на заданный товар или компанию
Инструмент для поиска отзывов пользователей на заданный товар или компанию Текстовый терминал
Текстовый терминал Bug report
Bug report Электронный ЮУрГУ. Видеоконференция. Таджикский язык
Электронный ЮУрГУ. Видеоконференция. Таджикский язык Технология создания буклета средствами специальной программы Microsoft Publixher
Технология создания буклета средствами специальной программы Microsoft Publixher Что такое информация?
Что такое информация? Презентация на тему Экстремизм в Интернете
Презентация на тему Экстремизм в Интернете  Микропроцессорные устройства. Лекция 4
Микропроцессорные устройства. Лекция 4 Основы алгоритмизации
Основы алгоритмизации О повышении потребительской грамотности. Как выбирать продукты
О повышении потребительской грамотности. Как выбирать продукты Предшественница ЭВМ-аналитическая машина
Предшественница ЭВМ-аналитическая машина Original graphic for inspiration
Original graphic for inspiration Администрирование информационных систем и веб-порталов
Администрирование информационных систем и веб-порталов Тузик и его друзья. Киностудия Маяк
Тузик и его друзья. Киностудия Маяк Нужен всем, спору нет, безопасный Интернет
Нужен всем, спору нет, безопасный Интернет Графический редактор
Графический редактор Системы хранения информации. Генератор опорных образов Mind-Surfing (урок 13)
Системы хранения информации. Генератор опорных образов Mind-Surfing (урок 13) Xamarin_Lect2
Xamarin_Lect2 Таблицы. Верстка сайта. Урок 9 2
Таблицы. Верстка сайта. Урок 9 2 История развития Интернета и всемирной паутины. Как Интернет повлиял на нашу жизнь
История развития Интернета и всемирной паутины. Как Интернет повлиял на нашу жизнь