Методика решения

Пример задания:
Сколько различных решений имеет логическое уравнение
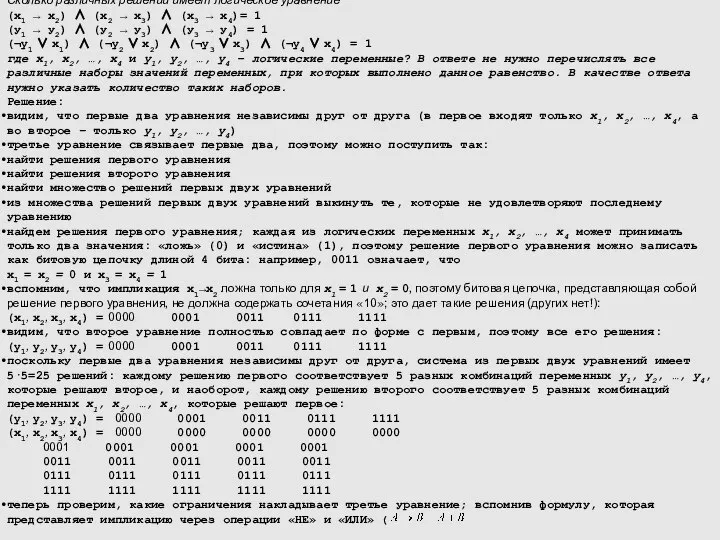
(x1 → x2) ∧ (x2 → x3) ∧ (x3 → x4)= 1
(у1 → у2) ∧ (у2 → у3) ∧ (у3 → у4) = 1
(¬y1 ∨ x1) ∧ (¬y2 ∨ x2) ∧ (¬y3 ∨ x3) ∧ (¬y4 ∨ x4) = 1
где x1, x2, …, x4 и y1, y2, …, y4 – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.
Решение:
видим, что первые два уравнения независимы друг от друга (в первое входят только x1, x2, …, x4, а во второе – только y1, y2, …, y4)
третье уравнение связывает первые два, поэтому можно поступить так:
найти решения первого уравнения
найти решения второго уравнения
найти множество решений первых двух уравнений
из множества решений первых двух уравнений выкинуть те, которые не удовлетворяют последнему уравнению
найдем решения первого уравнения; каждая из логических переменных x1, x2, …, x4 может принимать только два значения: «ложь» (0) и «истина» (1), поэтому решение первого уравнения можно записать как битовую цепочку длиной 4 бита: например, 0011 означает, что
x1 = x2 = 0 и x3 = x4 = 1
вспомним, что импликация x1→x2 ложна только для x1 = 1 и x2 = 0, поэтому битовая цепочка, представляющая собой решение первого уравнения, не должна содержать сочетания «10»; это дает такие решения (других нет!):
(x1, x2, x3, x4) = 0000 0001 0011 0111 1111
видим, что второе уравнение полностью совпадает по форме с первым, поэтому все его решения:
(y1, y2, y3, y4) = 0000 0001 0011 0111 1111
поскольку первые два уравнения независимы друг от друга, система из первых двух уравнений имеет 5·5=25 решений: каждому решению первого соответствует 5 разных комбинаций переменных y1, y2, …, y4, которые решают второе, и наоборот, каждому решению второго соответствует 5 разных комбинаций переменных x1, x2, …, x4, которые решают первое:
(y1, y2, y3, y4) = 0000 0001 0011 0111 1111
(x1, x2, x3, x4) = 0000 0000 0000 0000 0000
0001 0001 0001 0001 0001
0011 0011 0011 0011 0011
0111 0111 0111 0111 0111
1111 1111 1111 1111 1111
теперь проверим, какие ограничения накладывает третье уравнение; вспомнив формулу, которая представляет импликацию через операции «НЕ» и «ИЛИ» (

), можно переписать третье уравнение в виде
(y1 → x1) ∧ (y2 → x2) ∧ (y3 → x3) ∧ (y4 → x4) = 1
импликация y1→x1 ложна только для y1 = 1 и x1 = 0, следовательно, такая комбинация запрещена, потому что нарушает третье уравнение; таким образом, набору с y1 = 1:
(y1, y2, y3, y4) = 1111
соответствует, с учетом третьего уравнения, только одно решение первого, в котором x1 = 1
(y1, y2, y3, y4) = 1111
поэтому множество решений «редеет»:
(y1, y2, y3, y4) = 0000 0001 0011 0111 1111
(x1, x2, x3, x4) = 0000 0000 0000 0000
0001 0001 0001 0001
0011 0011 0011 0011
0111 0111 0111 0111
1111 1111 1111 1111 1111
аналогично двигаемся дальше по третьему уравнению; второй сомножитель равен 0, если импликация y2→x2 ложна, то есть только для y2 = 1 и x2 = 0, это «прореживает» предпоследний столбец:
(y1, y2, y3, y4) = 0000 0001 0011 0111 1111
(x1, x2, x3, x4) = 0000 0000 0000
0001 0001 0001
0011 0011 0011
0111 0111 0111 0111
1111 1111 1111 1111 1111
аналогично проверяем еще два ограничения, отбрасывая все решения, для которых y3 = 1 и x3 = 0, а также все решения, для которых y4 = 1 и x4 = 0:
(y1, y2, y3, y4) = 0000 0001 0011 0111 1111
(x1, x2, x3, x4) = 0000
0001 0001
0011 0011 0011
0111 0111 0111 0111
1111 1111 1111 1111 1111
итак, остается одно решение при (y1, y2, y3, y4)=1111, два решения при (y1, y2, y3, y4)=0111, три решения при(y1, y2, y3, y4)=0011, четыре решения при(y1, y2, y3, y4)=0001 и 5 решений при (y1, y2, y3, y4)=0000
всего решений 1+2+3+4+5=15.

88Сколько различных решений имеет система уравнений?
(x1 → x2) ∧ (x2 → x3) ∧ (x3 → x4) = 1
(у1 → у2) ∧ (у2 → у3) ∧ (у3 → у4) = 1
(¬y1 ∨ x1) ∧ (¬y2 ∨ x2) ∧ (¬y3 ∨ x3) ∧ (¬y4 ∨ x4) = 1
где x1,x2,…,x4, у1,у2,…,у4 – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.
89Сколько различных решений имеет система уравнений?
(x1 → x2) ∧ (x2 → x3) ∧ (x3 → x4) = 1
(у1 → у2) ∧ (у2 → у3) ∧ (у3 → у4) = 1
(¬y1 ∨ x1) ∧ (¬x2 ∨ y2) ∧ (¬y3 ∨ x3) ∧ (¬x4 ∨ y4) = 1
где x1,x2,…,x4, у1,у2,…,у4 – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.
90Сколько различных решений имеет система уравнений?
(x1 → x2) ∧ (x2 → x3) ∧ (x3 → x4) = 1
(у1 → у2) ∧ (у2 → у3) ∧ (у3 → у4) = 1
(¬y1 ∨ x1) ∧ (¬x2 ∨ y2) = 1
где x1,x2,…,x4, у1,у2,…,у4 – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.
91Сколько различных решений имеет система уравнений?
(x1 → x2) ∧ (x2 → x3) ∧ (x3 → x4) = 1
(у1 → у2) ∧ (у2 → у3) ∧ (у3 → у4) = 1
(¬y1 ∨ x1) ∧ (¬y2 ∨ x2) = 1
где x1,x2,…,x4, у1,у2,…,у4 – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.