Содержание
- 2. Моделирование § 13. Модели и моделирование
- 3. Что такое модель? модели чего? автомобиль Земля кристаллическая решётка корабль дом оригиналы объекты (самолет, дом, ядро
- 4. Что такое модель? оригинал не существует древний Египет последствия ядерной войны (Н.Н. Моисеев, 1966) исследование оригинала
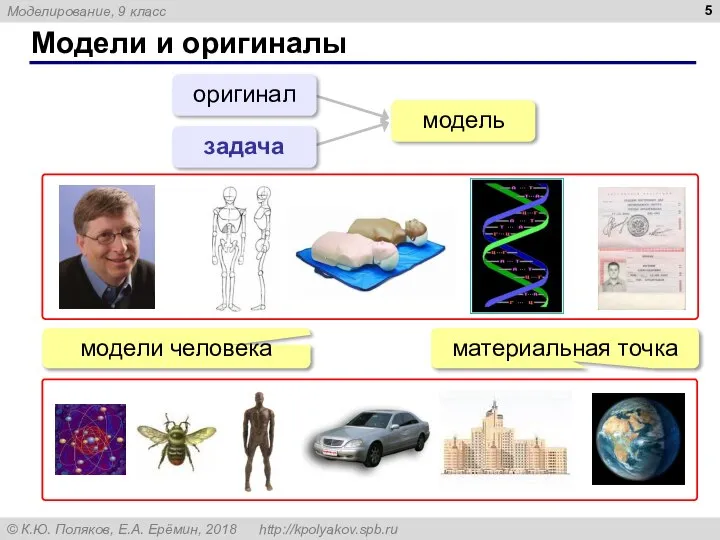
- 5. Модели и оригиналы оригинал задача модель материальная точка модели человека
- 6. Модели и моделирование Модель – это объект, который обладает существенными свойствами другого объекта, процесса или явления
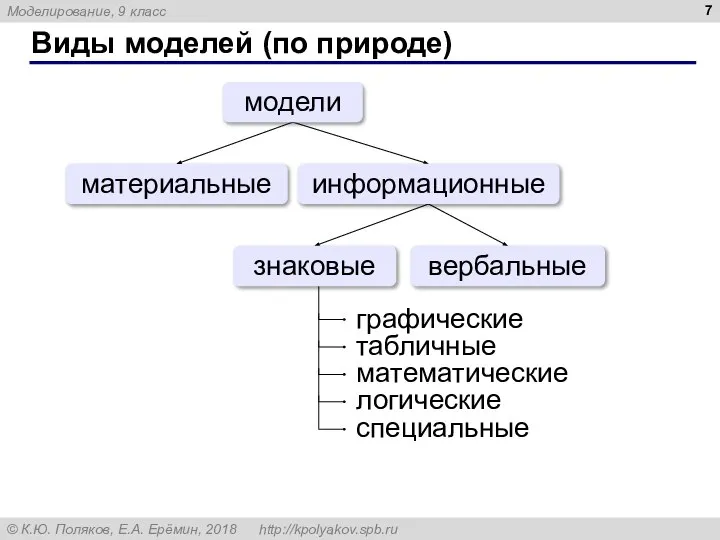
- 7. Виды моделей (по природе) материальные вербальные модели знаковые информационные
- 8. Виды моделей (по фактору времени) статические – описывают оригинал в заданный момент времени силы, действующие на
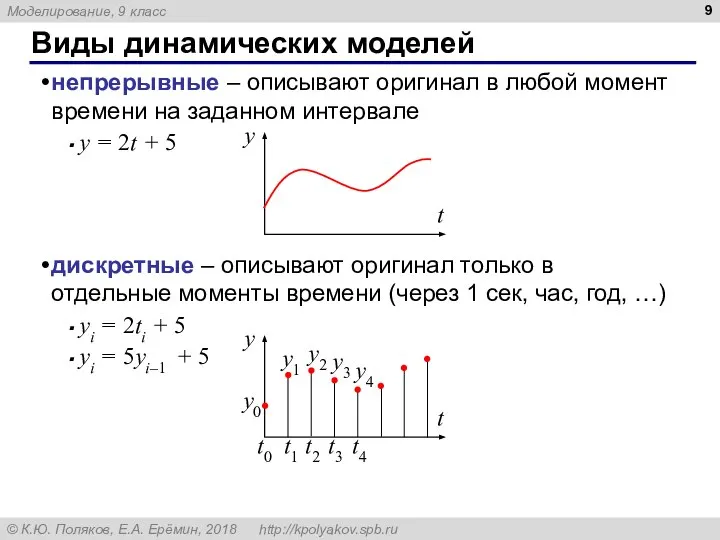
- 9. Виды динамических моделей непрерывные – описывают оригинал в любой момент времени на заданном интервале y =
- 10. Виды моделей (по характеру связей) детерминированные – при одинаковых исходных данных всегда получается тот же результат
- 11. Имитационные модели нельзя заранее вычислить или предсказать поведение системы, но можно имитировать её реакцию на внешние
- 12. Игровые модели экономические ситуации военные действия спортивные игры тренинги персонала Игровые модели учитывают действия противников.
- 13. Адекватность Адекватность – это совпадение существенных свойств модели и оригинала в данной задаче. Модель всегда отличается
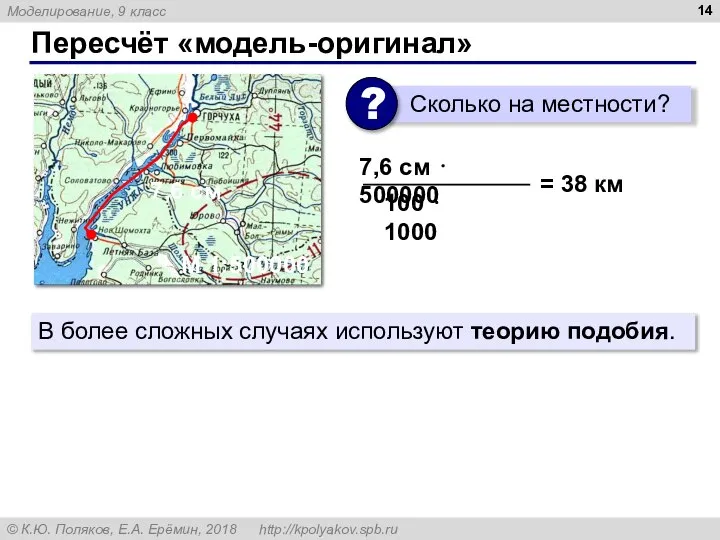
- 14. Пересчёт «модель-оригинал» 7,6 см М 1:500000 7,6 см ⋅ 500000 = 38 км В более сложных
- 15. Моделирование § 14. Математическое моделирование
- 16. I. Постановка задачи Хорошо поставленная задача: описаны все связи между исходными данными и результатом известны все
- 17. I. Постановка задачи Мальчик Вася в синей кепке бросает белый мяч со скоростью 12 м/с. Когда
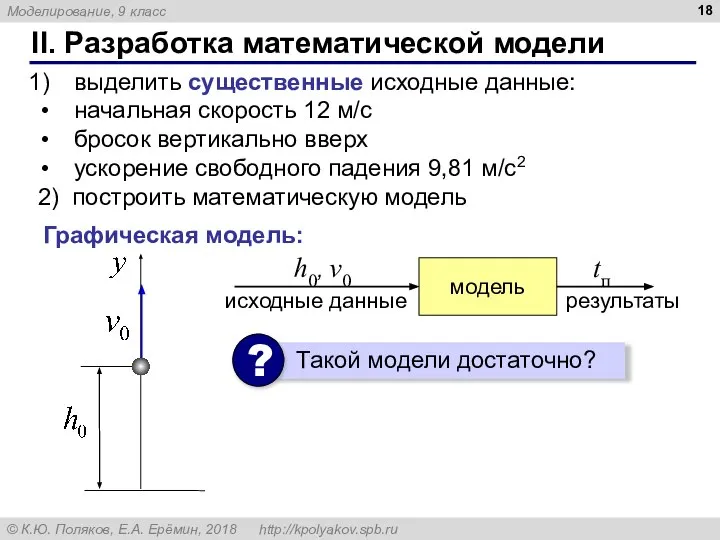
- 18. II. Разработка математической модели выделить существенные исходные данные: начальная скорость 12 м/с бросок вертикально вверх ускорение
- 19. II. Разработка математической модели Формализация: Мяч упал: Ещё допущения: мяч – материальная точка нет сопротивления воздуха
- 20. III. Тестирование модели Тестирование – это проверка модели на простых исходных данных с известным результатом. •
- 21. IV. Построение компьютерной модели алг Полёт нач вещ h0=1.5, v0=12, g=9.81 вещ a, b, c, D,
- 22. IV. Построение компьютерной модели program Polet; var h0, v0, g: real; a, b, c, D, t1,
- 23. IV. Построение компьютерной модели from math import sqrt h0 = 1.5 v0 = 12 g =
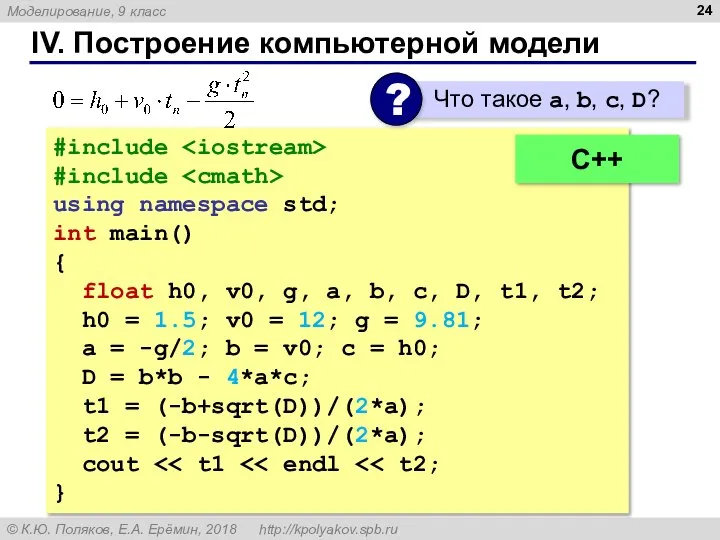
- 24. IV. Построение компьютерной модели #include #include using namespace std; int main() { float h0, v0, g,
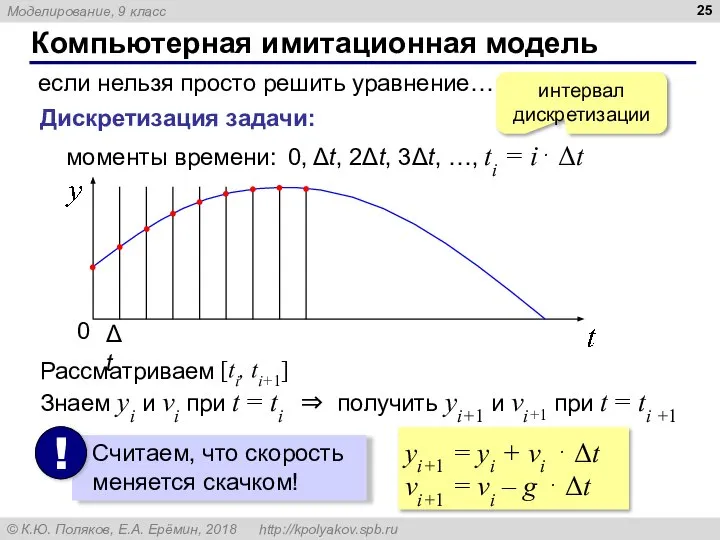
- 25. Компьютерная имитационная модель если нельзя просто решить уравнение… Дискретизация задачи: моменты времени: 0, Δt, 2Δt, 3Δt,
- 26. Компьютерная имитационная модель алг Полёт-2 нач вещ h0=1.5, v0=12, g=9.81 вещ y, v, t, dt=0.01 y:=
- 27. Компьютерная имитационная модель program Polet_2; var h0, v0, g: real; y, v, t, dt: real; begin
- 28. Компьютерная имитационная модель h0 = 1.5 v0 = 12 g = 9.81 dt = 0.01 y
- 29. Компьютерная имитационная модель #include using namespace std; int main() { float h0, y, v0, v, g,
- 30. V. Эксперимент с моделью Эксперимент – это исследование модели при тех исходных данных, которые нас интересуют
- 31. VI. Анализ результатов Возможные выводы: задача решена, модель адекватна необходимо изменить алгоритм или условия моделирования необходимо
- 32. Моделирование § 15. Табличные модели. Диаграммы
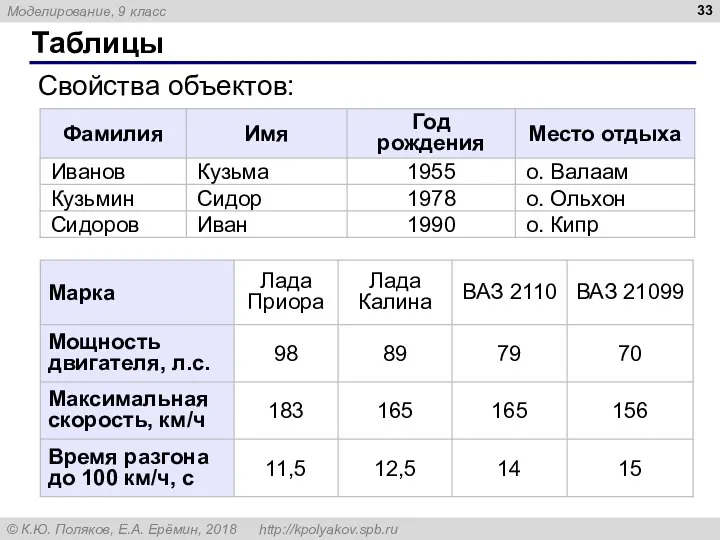
- 33. Таблицы Свойства объектов:
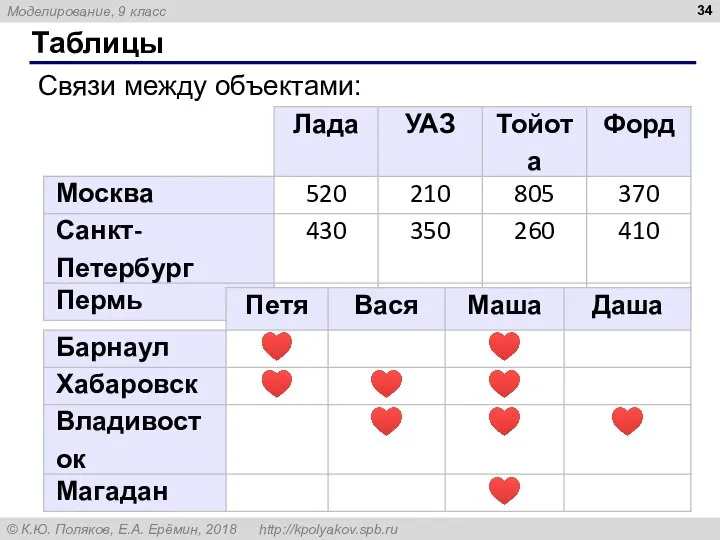
- 34. Таблицы Связи между объектами:
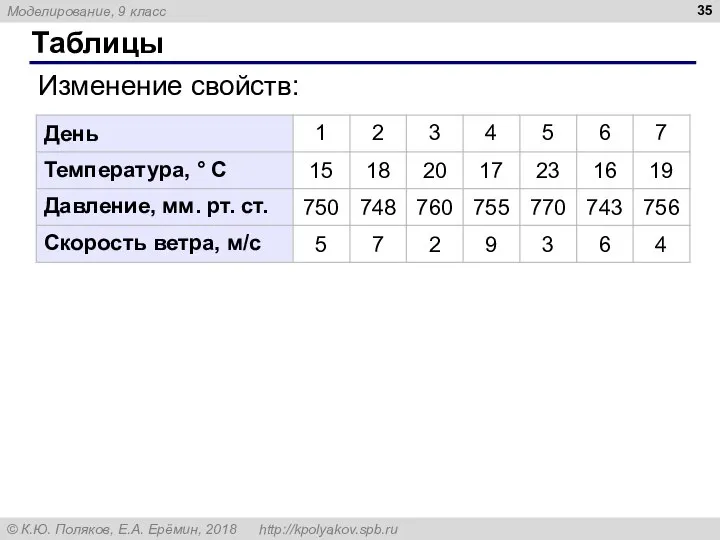
- 35. Таблицы Изменение свойств:
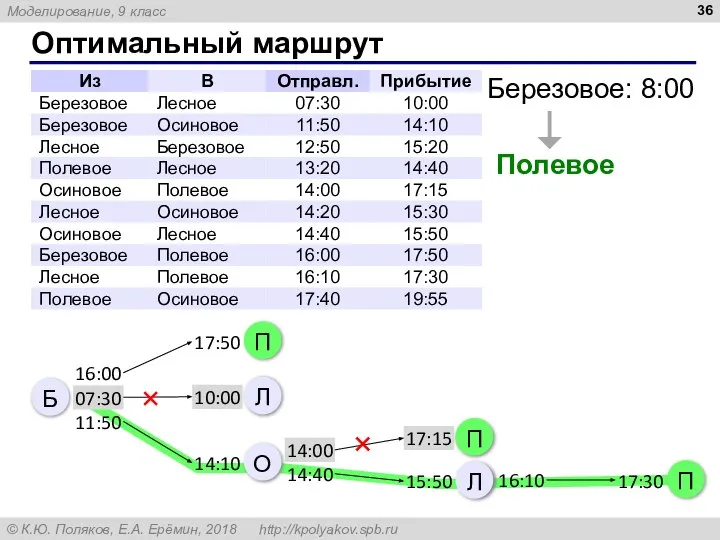
- 36. Оптимальный маршрут Березовое: 8:00 Полевое Б 16:00 07:30 11:50 14:00 14:40 16:10
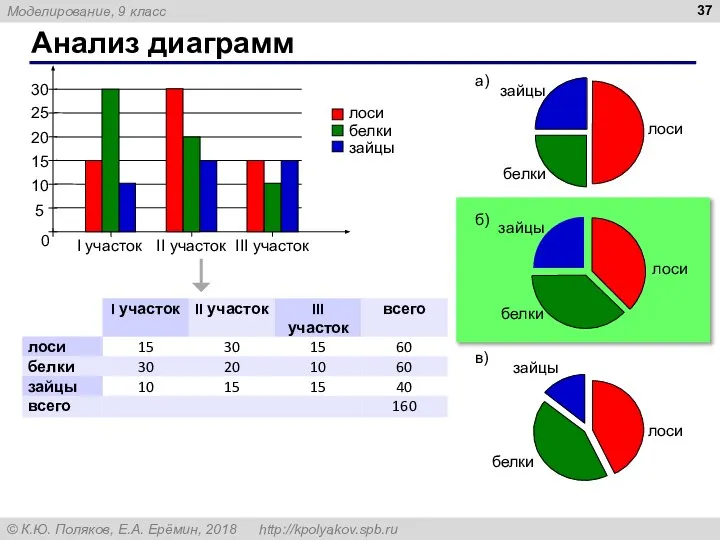
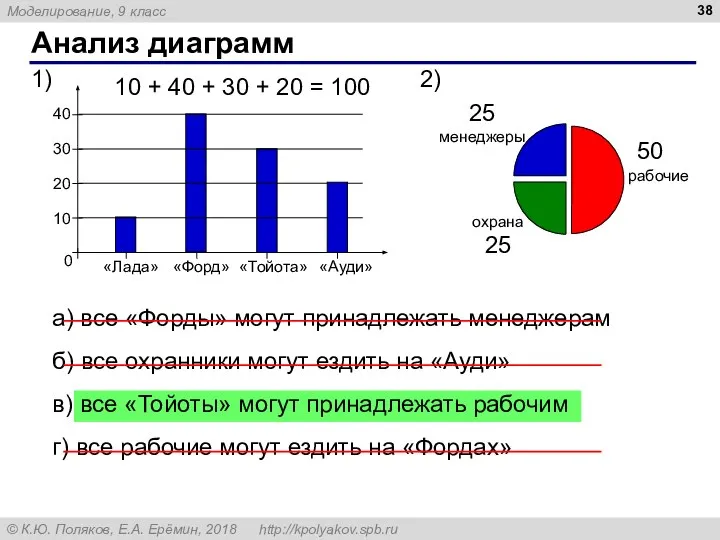
- 37. Анализ диаграмм
- 38. Анализ диаграмм а) все «Форды» могут принадлежать менеджерам б) все охранники могут ездить на «Ауди» в)
- 39. Моделирование § 16. Списки и деревья
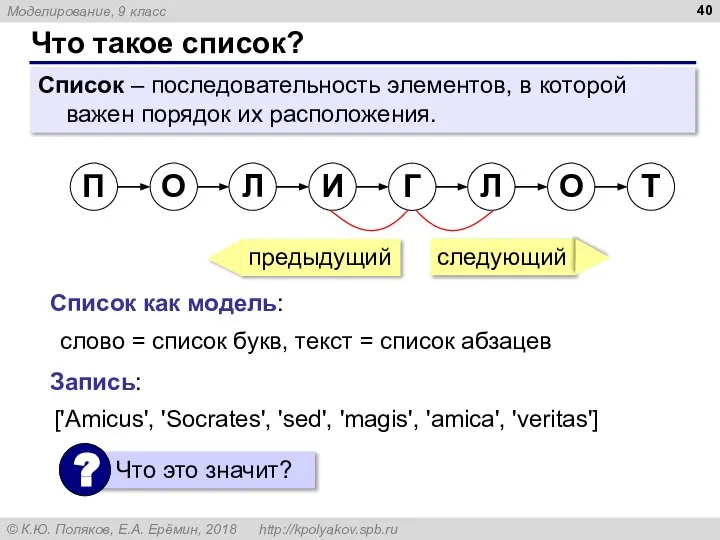
- 40. Что такое список? Список – последовательность элементов, в которой важен порядок их расположения. ['Amicus', 'Socrates', 'sed',
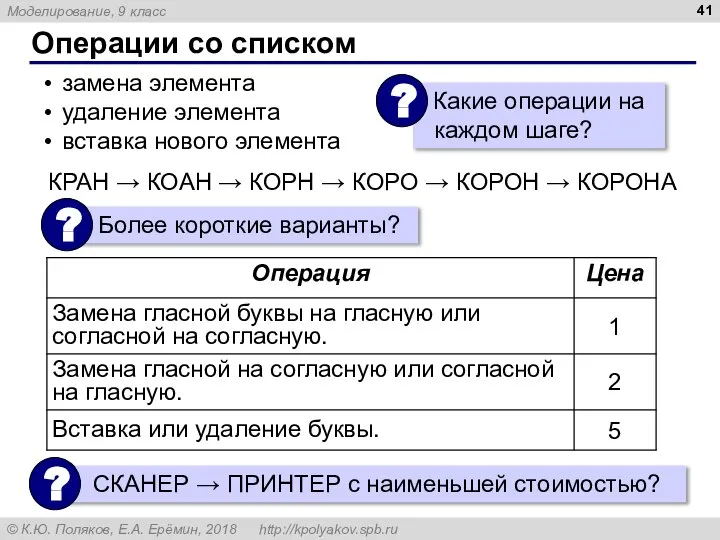
- 41. Операции со списком замена элемента удаление элемента вставка нового элемента КРАН → КОАН → КОРН →
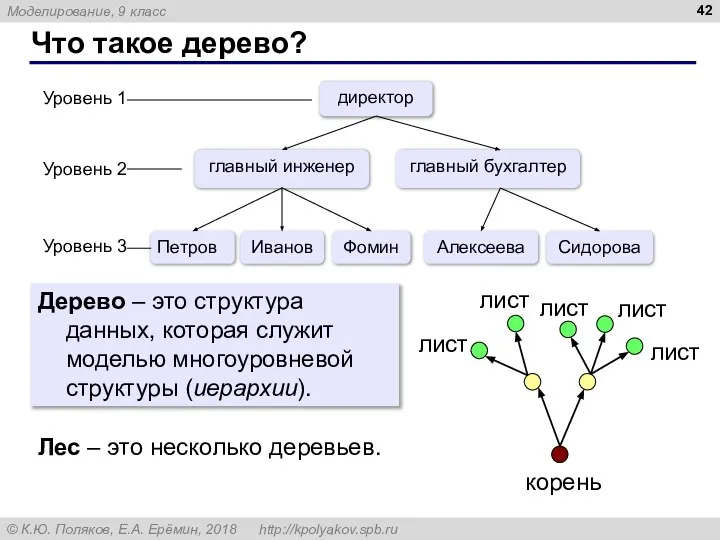
- 42. Что такое дерево? Дерево – это структура данных, которая служит моделью многоуровневой структуры (иерархии). Лес –
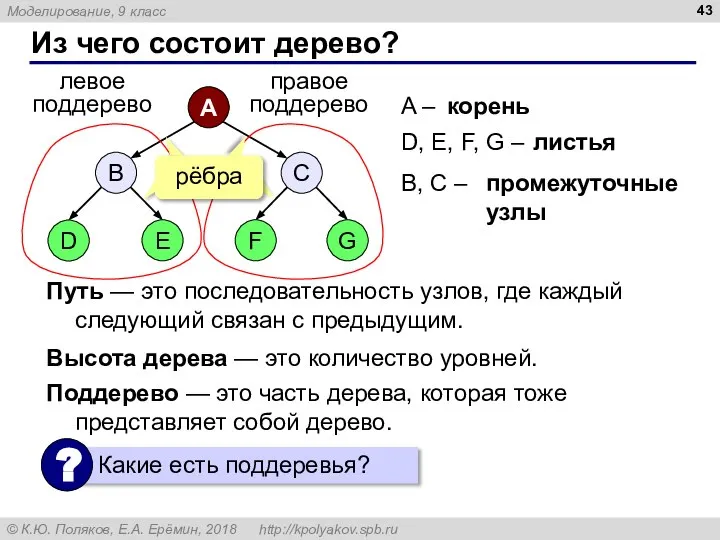
- 43. Из чего состоит дерево? A – D, E, F, G – корень листья B, C –
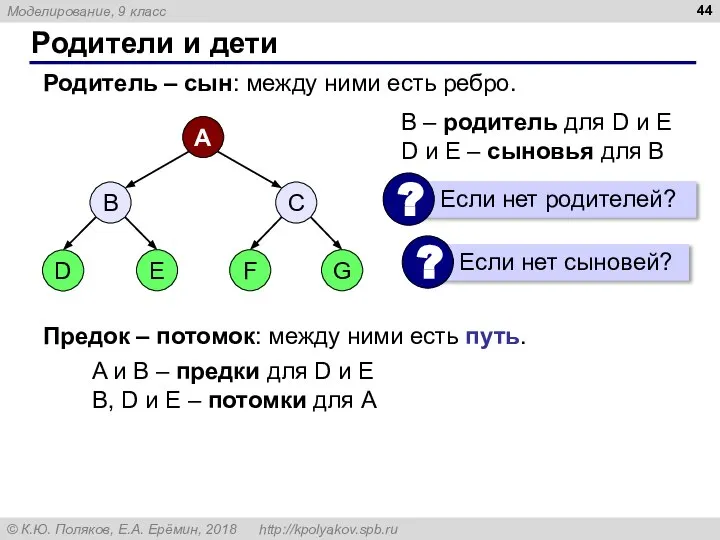
- 44. Родители и дети B – родитель для D и E D и E – сыновья для
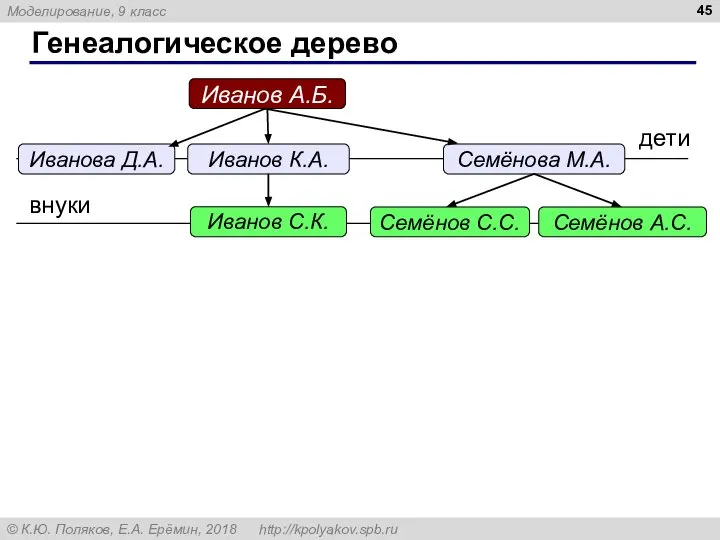
- 45. Генеалогическое дерево Иванов А.Б. Иванова Д.А. Семёнова М.А. Иванов К.А. Семёнов C.C. Семёнов А.C. Иванов C.К.
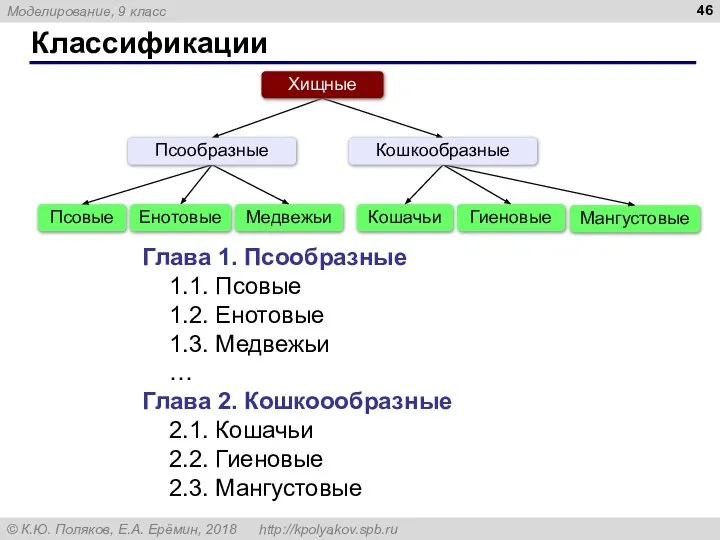
- 46. Классификации Глава 1. Псообразные 1.1. Псовые 1.2. Енотовые 1.3. Медвежьи … Глава 2. Кошкоообразные 2.1. Кошачьи
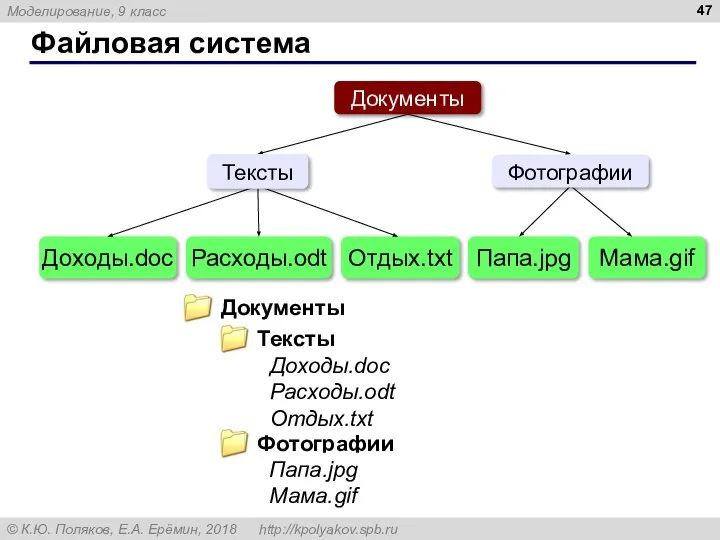
- 47. Файловая система
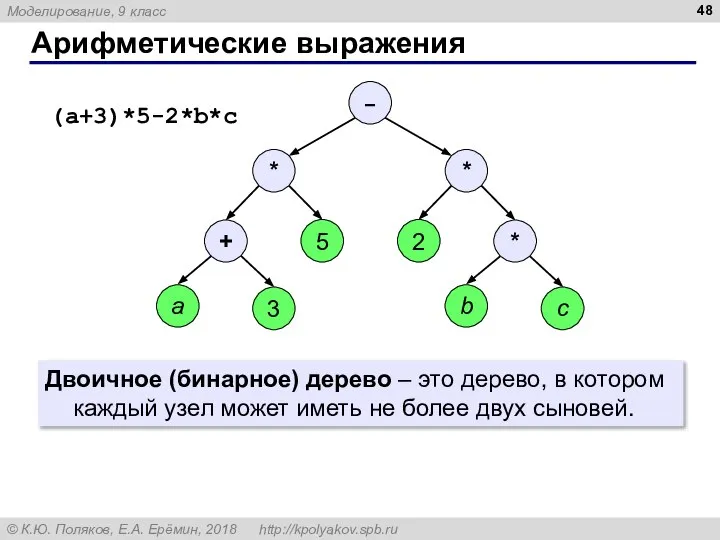
- 48. Арифметические выражения Двоичное (бинарное) дерево – это дерево, в котором каждый узел может иметь не более
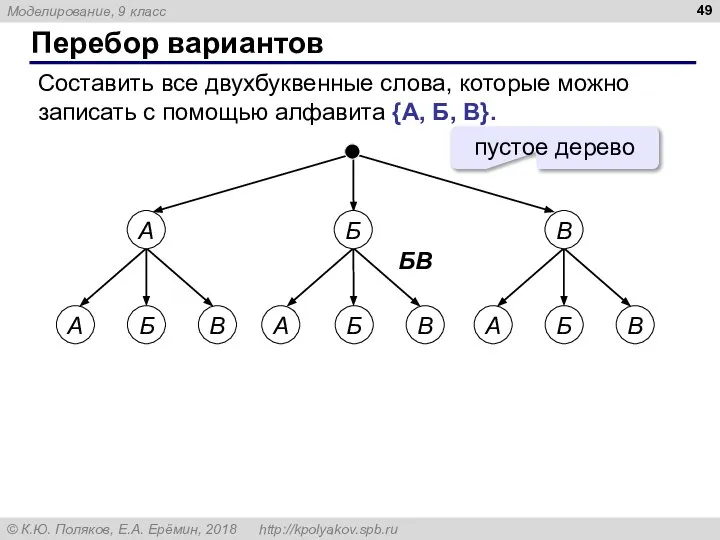
- 49. Перебор вариантов Составить все двухбуквенные слова, которые можно записать с помощью алфавита {A, Б, В}. Б
- 50. Перебор вариантов Разведчик выяснил, что ключ к замку от сейфа состоит из трёх символов, причём могут
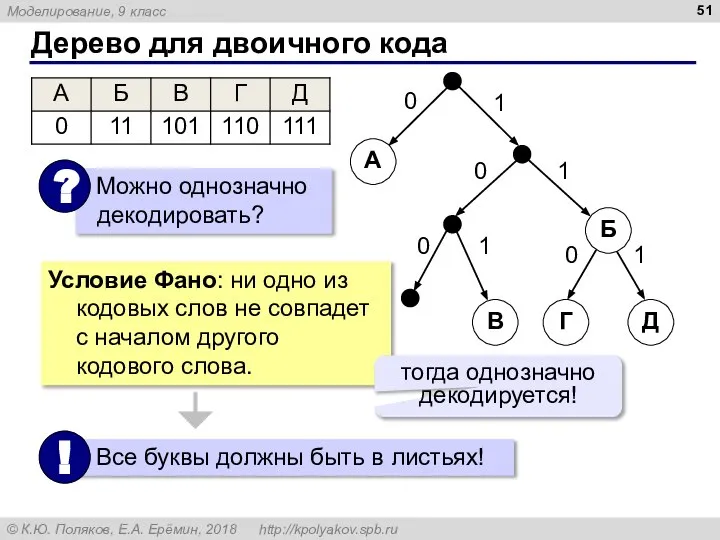
- 51. Дерево для двоичного кода Г Д Б В А 0 1 1 0 0 1 0
- 52. Моделирование § 17. Графы
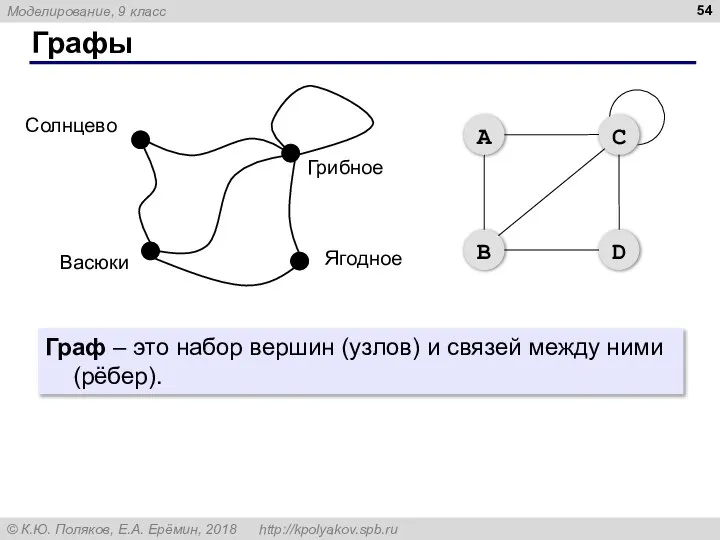
- 53. Графы «От посёлка Васюки три дороги идут в посёлки Солнцево, Грибное и Ягодное. Между Солнцевым и
- 54. Графы Граф – это набор вершин (узлов) и связей между ними (рёбер).
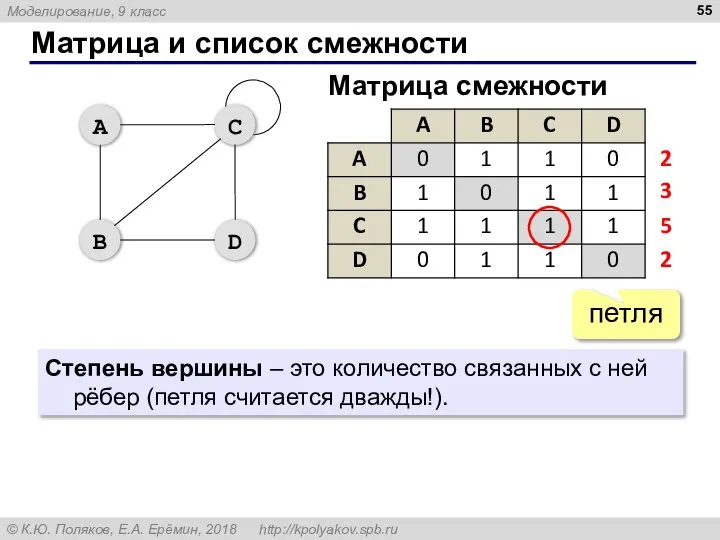
- 55. Матрица и список смежности петля Матрица смежности Степень вершины – это количество связанных с ней рёбер
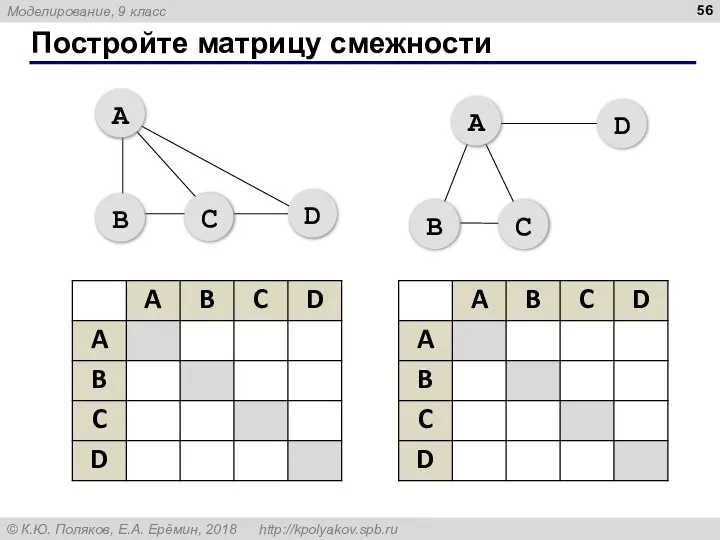
- 56. Постройте матрицу смежности
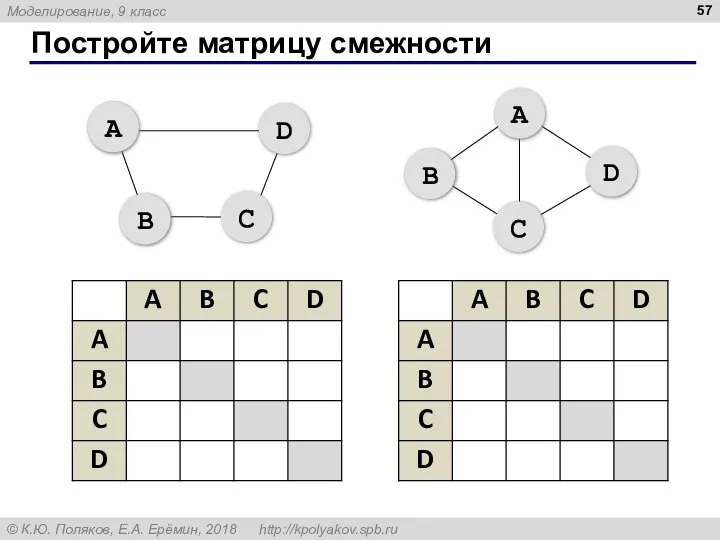
- 57. Постройте матрицу смежности
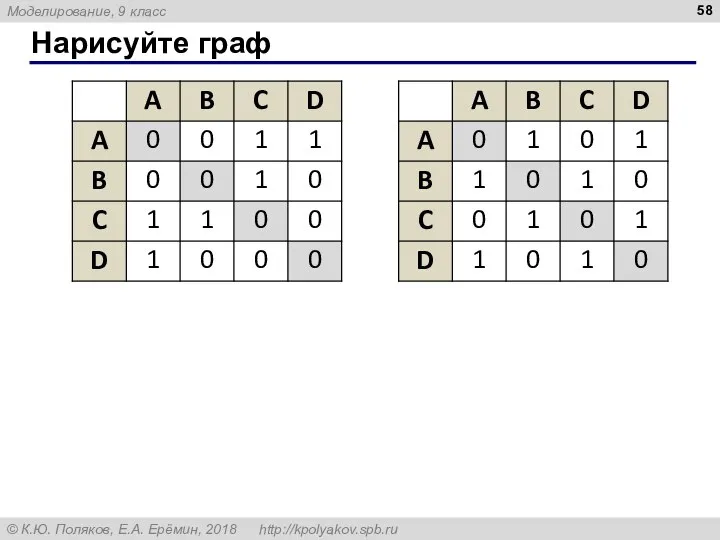
- 58. Нарисуйте граф
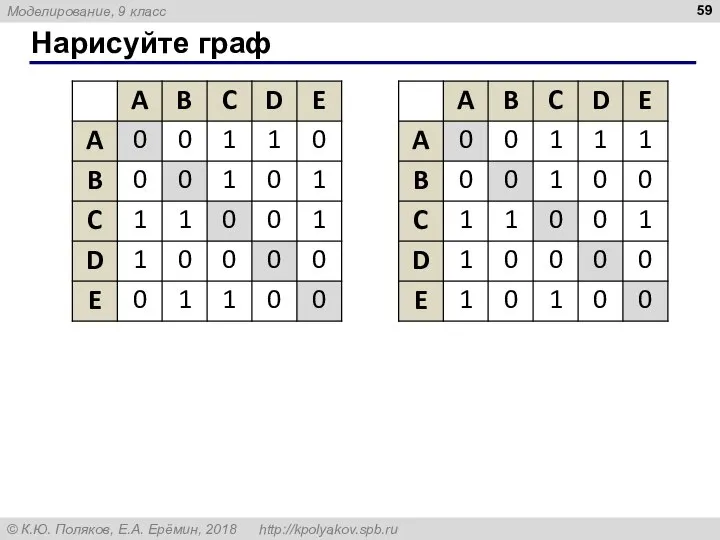
- 59. Нарисуйте граф
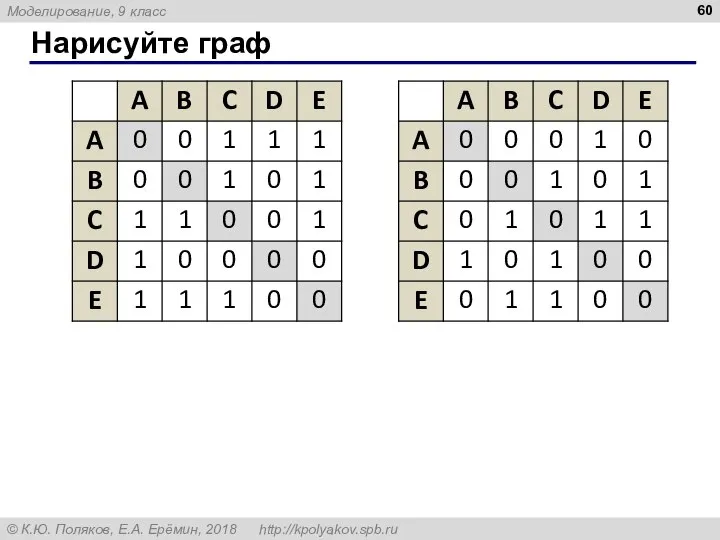
- 60. Нарисуйте граф
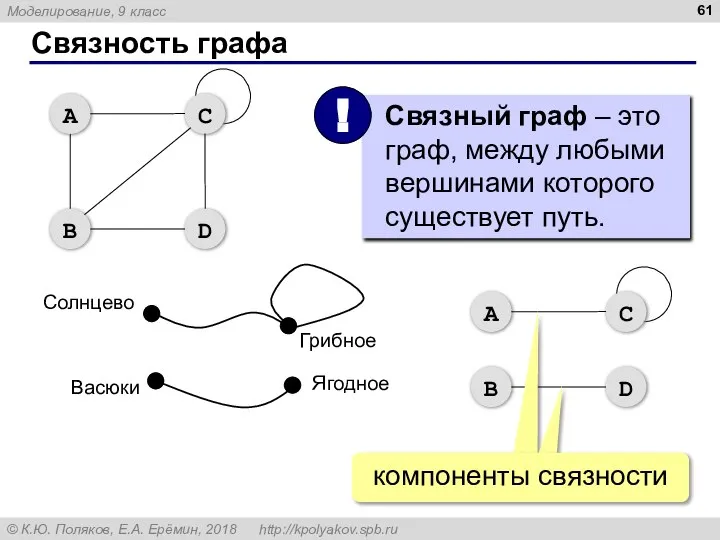
- 61. Связность графа
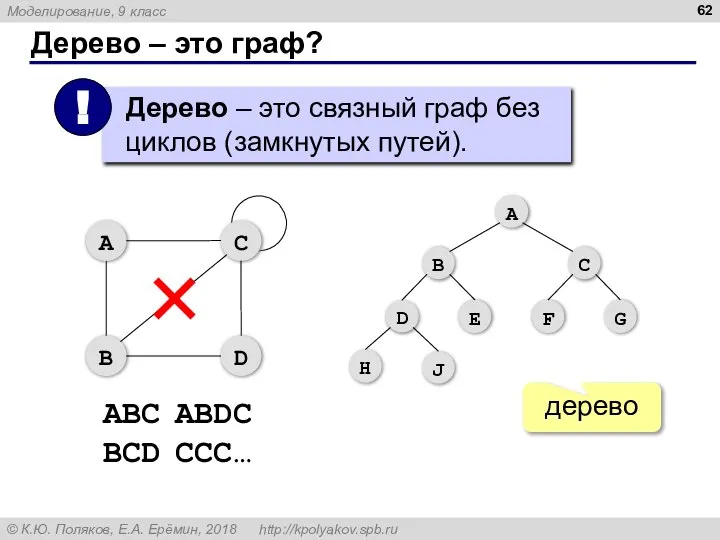
- 62. Дерево – это граф? дерево ABC ABDC BCD CCC…
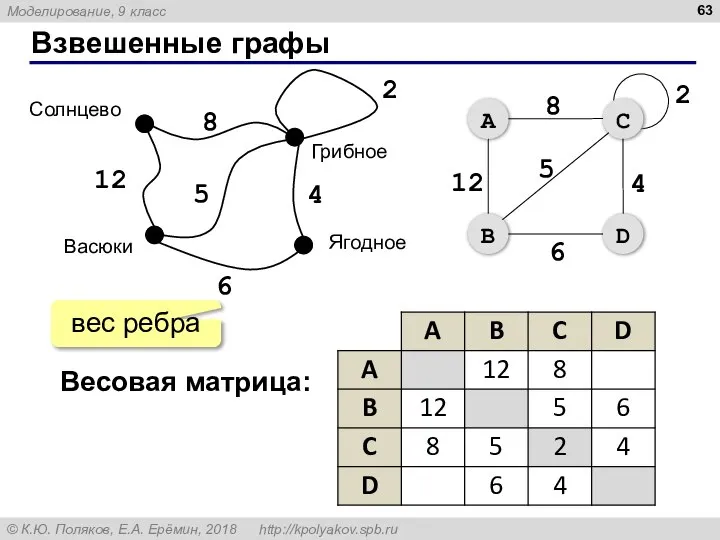
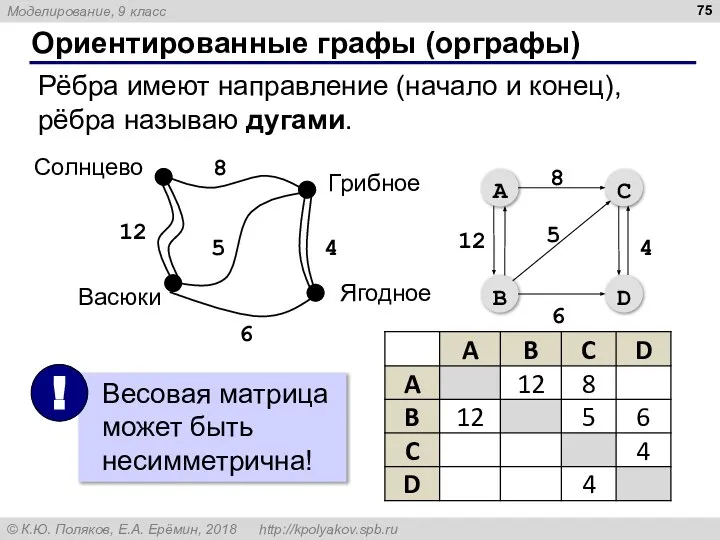
- 63. Взвешенные графы 12 8 2 5 4 6 Весовая матрица: вес ребра
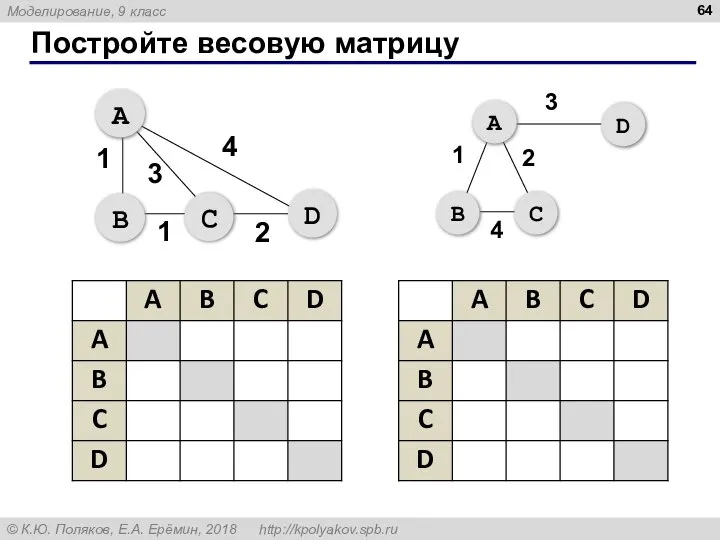
- 64. Постройте весовую матрицу
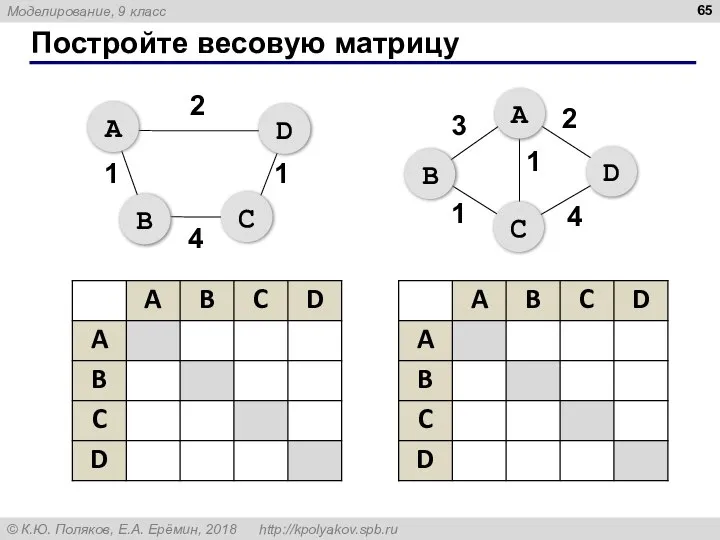
- 65. Постройте весовую матрицу
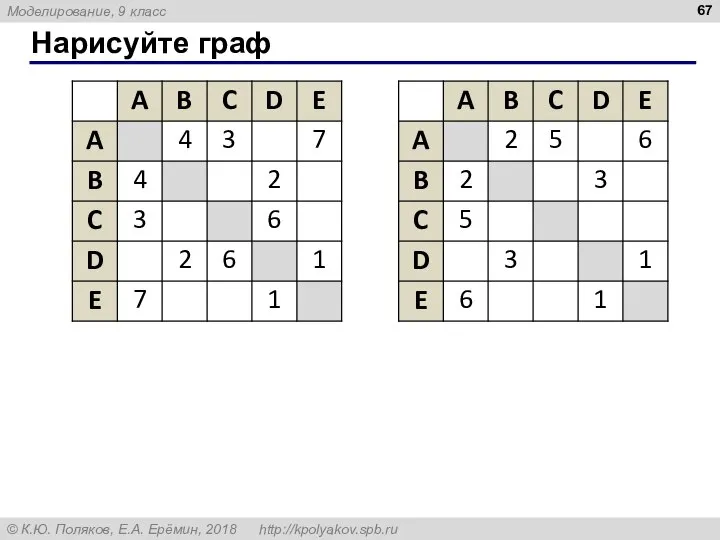
- 66. Нарисуйте граф
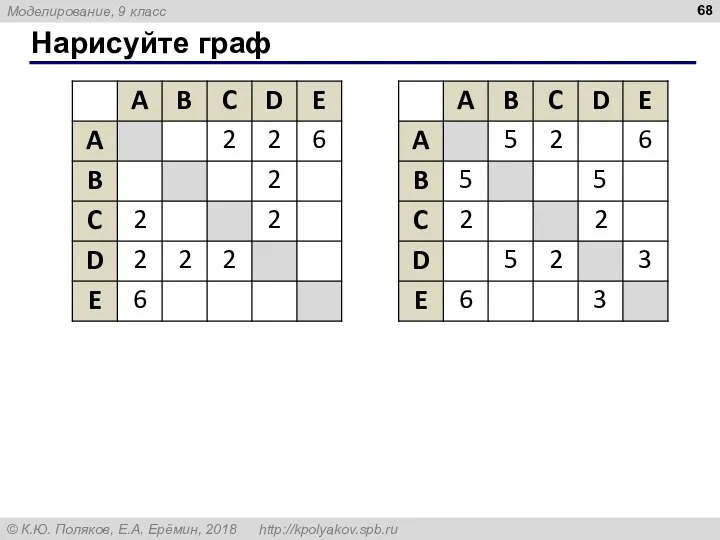
- 67. Нарисуйте граф
- 68. Нарисуйте граф
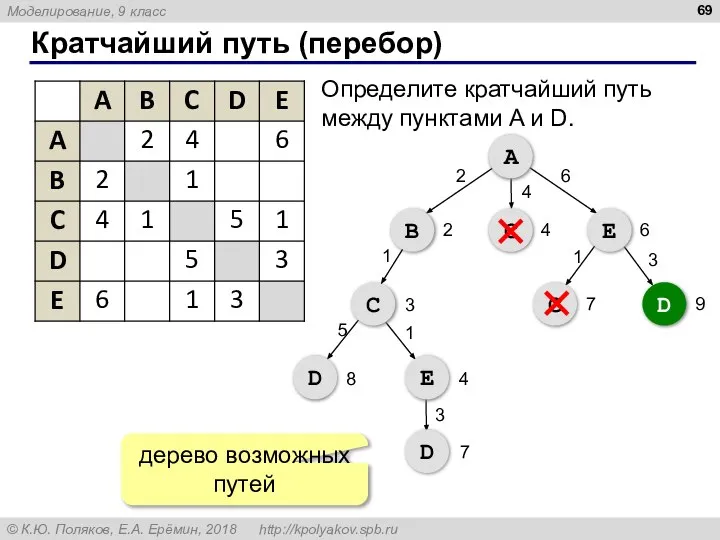
- 69. Кратчайший путь (перебор) A B С E С D С D E D 2 4 6
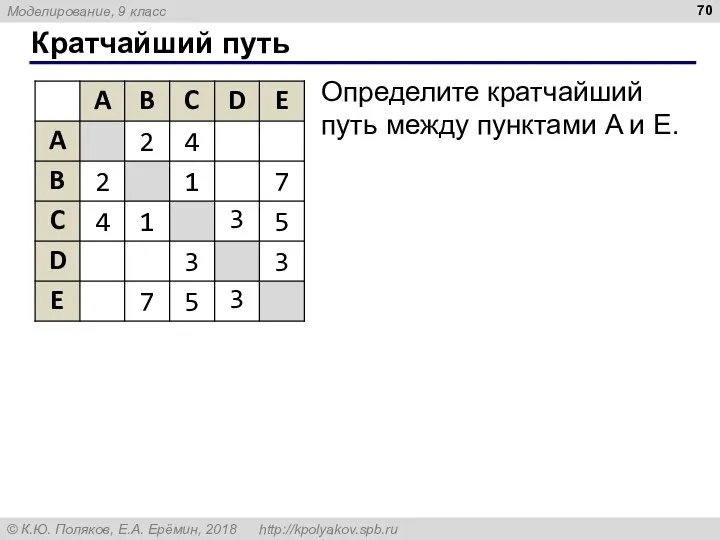
- 70. Кратчайший путь Определите кратчайший путь между пунктами A и E.
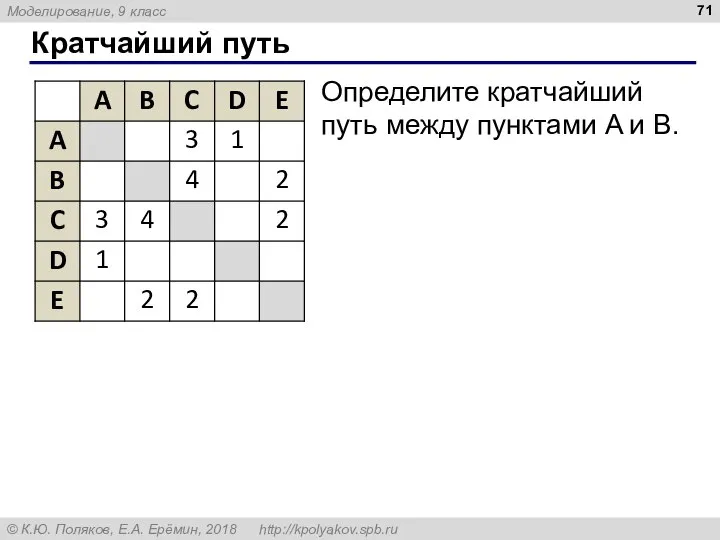
- 71. Кратчайший путь Определите кратчайший путь между пунктами A и B.
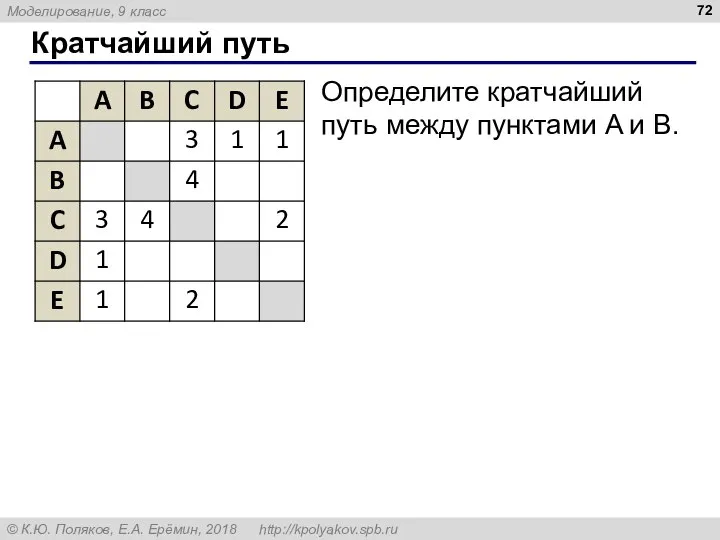
- 72. Кратчайший путь Определите кратчайший путь между пунктами A и B.
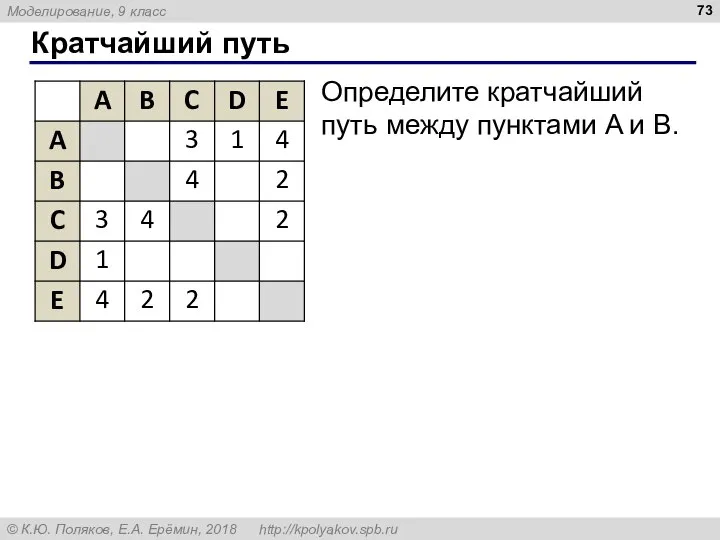
- 73. Кратчайший путь Определите кратчайший путь между пунктами A и B.
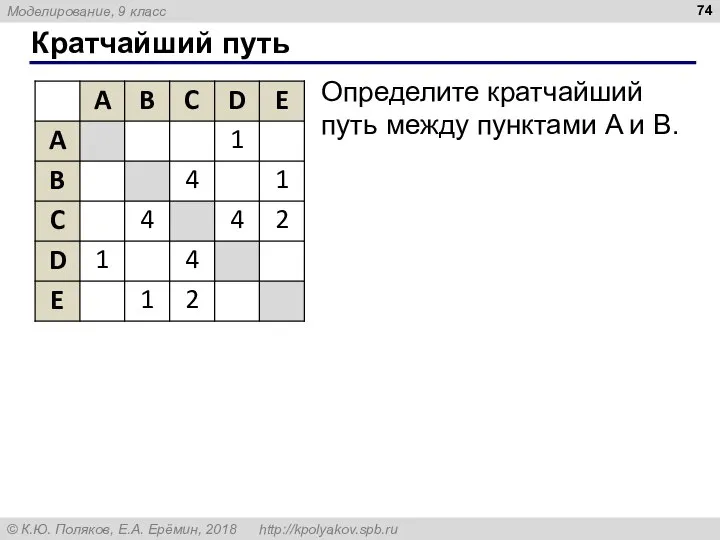
- 74. Кратчайший путь Определите кратчайший путь между пунктами A и B.
- 75. Ориентированные графы (орграфы) Рёбра имеют направление (начало и конец), рёбра называю дугами.
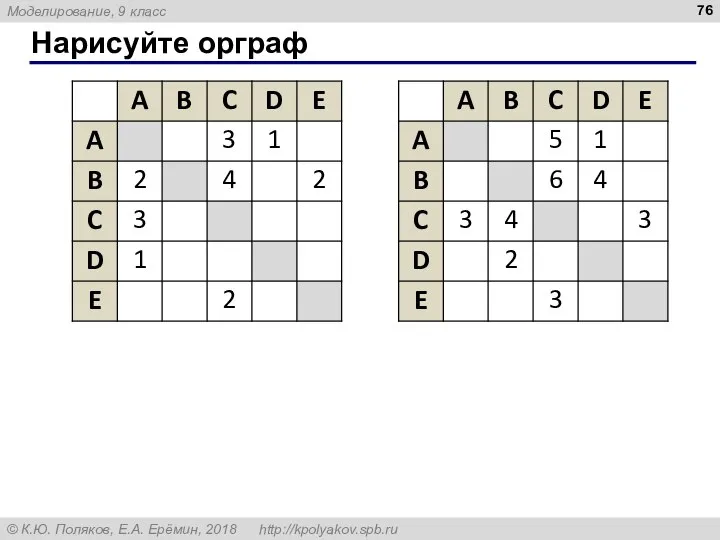
- 76. Нарисуйте орграф
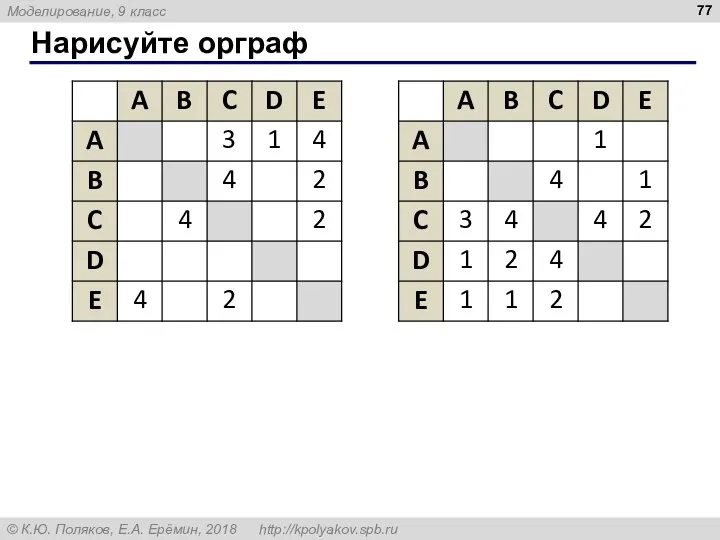
- 77. Нарисуйте орграф
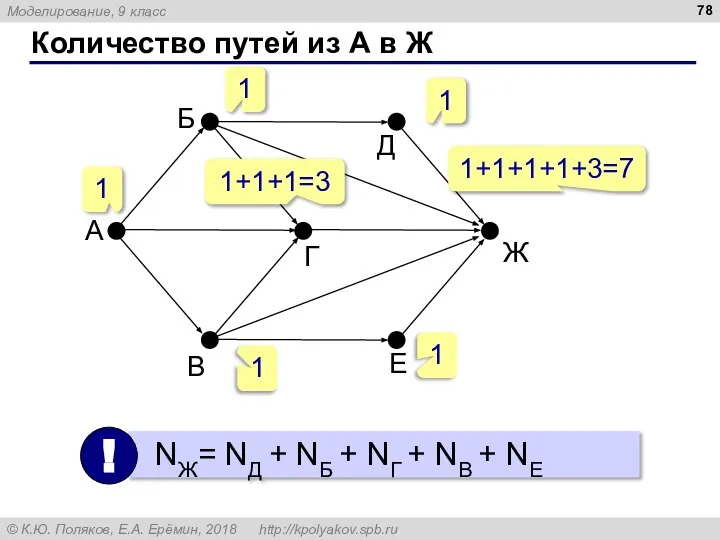
- 78. Количество путей из А в Ж 1 1 1 1+1+1=3 1 1+1+1+1+3=7 1
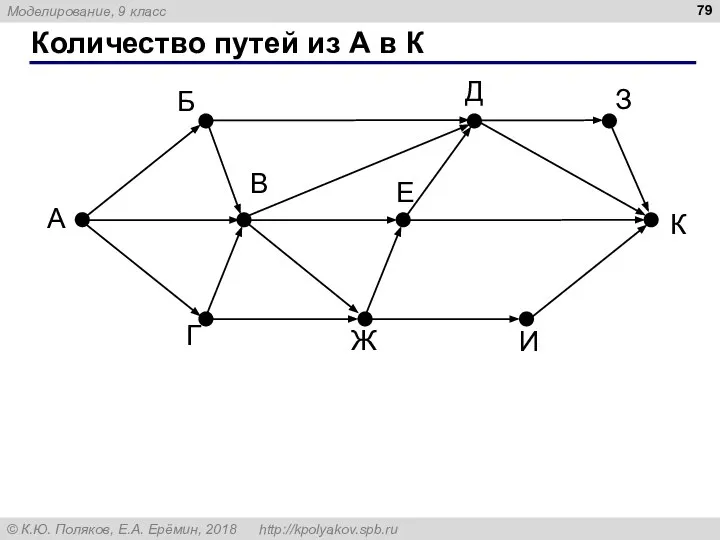
- 79. Количество путей из А в К
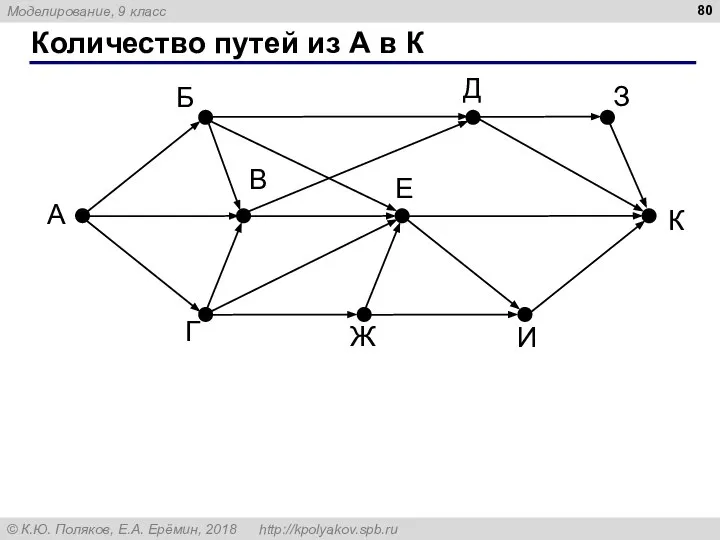
- 80. Количество путей из А в К
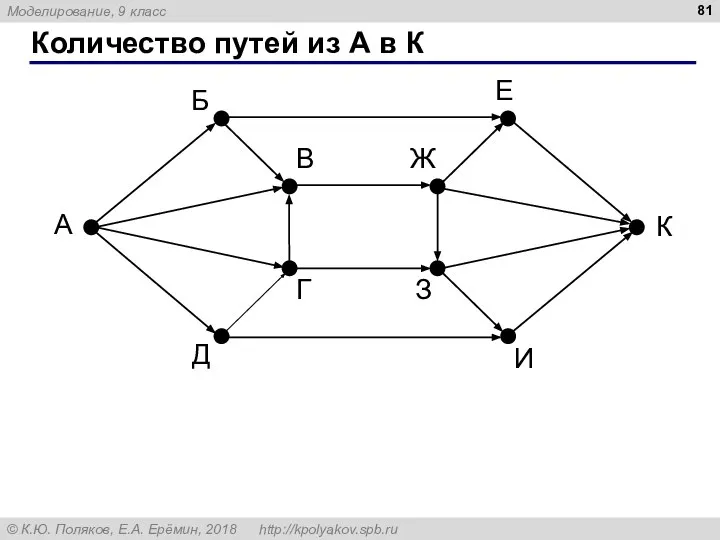
- 81. Количество путей из А в К
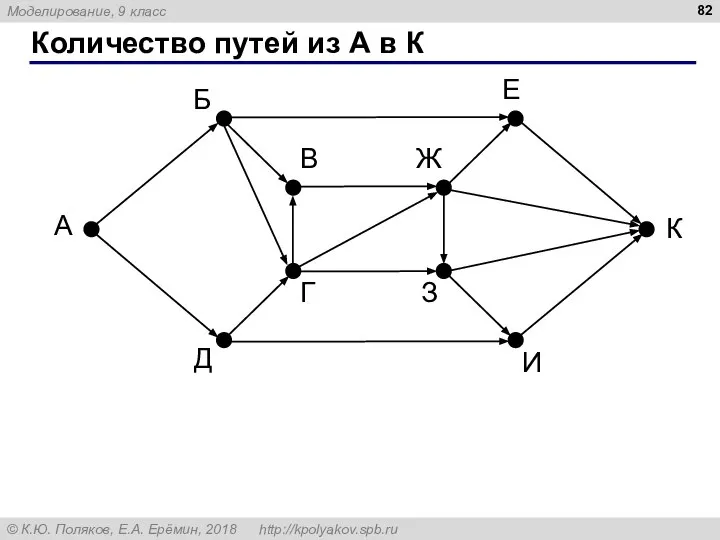
- 82. Количество путей из А в К
- 83. Моделирование § 18. Игровые стратегии
- 84. Что такое игровая модель? Игровая модель — это модель, которая описывает соперничество двух (или более) сторон,
- 85. Выигрышные и проигрышные позиции игра без ничьих… Выигрышная позиция — это такая позиция, в которой игрок,
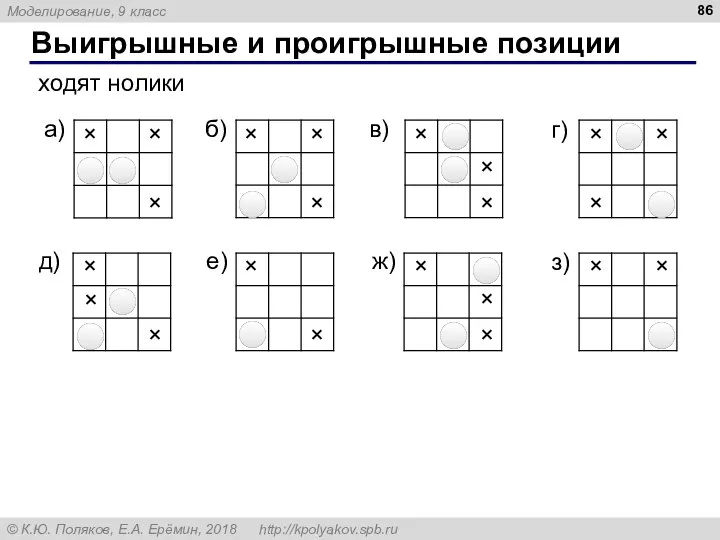
- 86. Выигрышные и проигрышные позиции ходят нолики
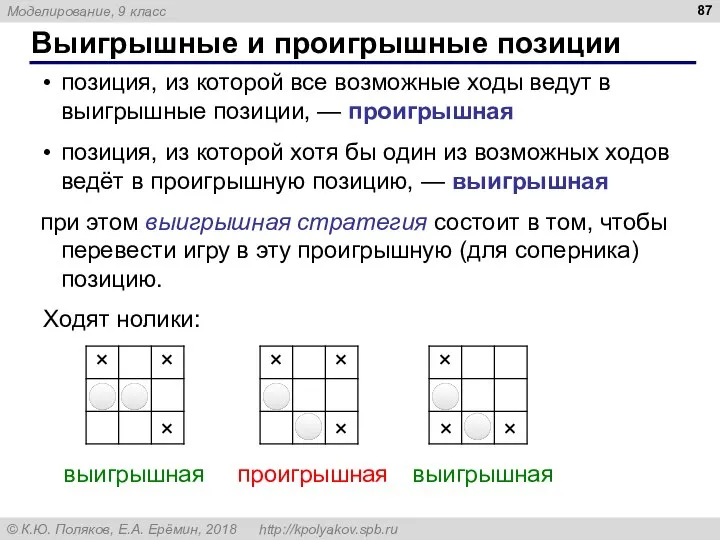
- 87. Выигрышные и проигрышные позиции позиция, из которой все возможные ходы ведут в выигрышные позиции, — проигрышная
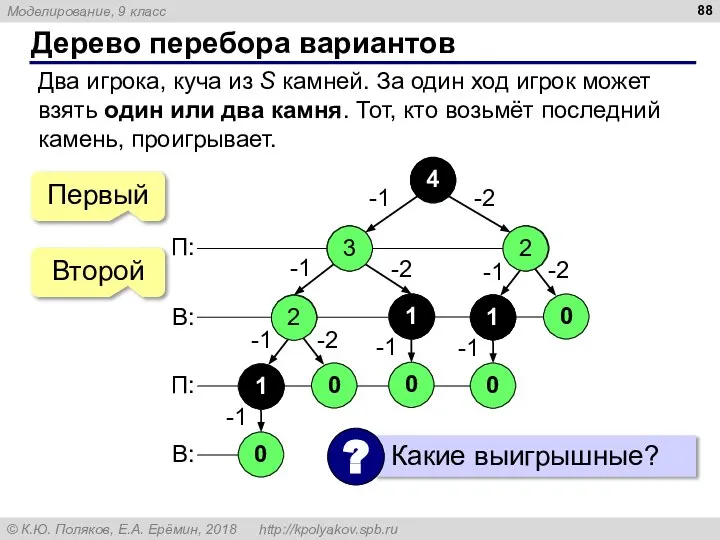
- 88. Дерево перебора вариантов Два игрока, куча из S камней. За один ход игрок может взять один
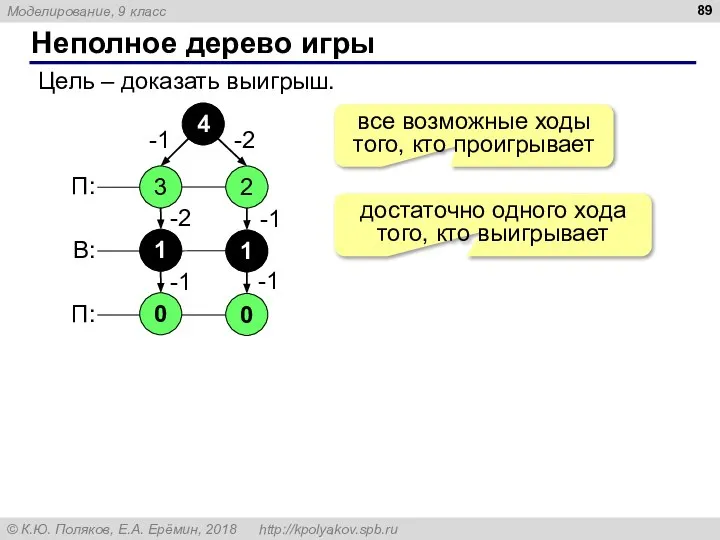
- 89. Неполное дерево игры Цель – доказать выигрыш. 4 все возможные ходы того, кто проигрывает достаточно одного
- 90. Таблица позиций П1 В1 В1 П2 В2 В2 П3 В3 В3 П4 Нужно оставлять сопернику N
- 91. Конец фильма ПОЛЯКОВ Константин Юрьевич д.т.н., учитель информатики ГБОУ СОШ № 163, г. Санкт-Петербург [email protected] ЕРЕМИН
- 93. Скачать презентацию

































 HRM and its challenges
HRM and its challenges Тесты по информатике и информационным технологиям в юриспруденции
Тесты по информатике и информационным технологиям в юриспруденции Популярные компьютерные игры
Популярные компьютерные игры Компьютерная графика
Компьютерная графика Кодирование информации
Кодирование информации Мобильное рабочее место Единой корпоративной автоматизированной системы управления инфраструктурой дирекции по ремонту пути
Мобильное рабочее место Единой корпоративной автоматизированной системы управления инфраструктурой дирекции по ремонту пути Библиографическая запись. Библиографическое описание
Библиографическая запись. Библиографическое описание Презентация на тему Информационные объекты Windows: файлы и папки
Презентация на тему Информационные объекты Windows: файлы и папки  Microsoft Entourage
Microsoft Entourage Как определить пользу и вред компьютерных игр
Как определить пользу и вред компьютерных игр Системы управления базами данных. Реляционная модель данных
Системы управления базами данных. Реляционная модель данных Учёба занимает всё свободное время? на любимые игры нет времени? скачай это приложение!
Учёба занимает всё свободное время? на любимые игры нет времени? скачай это приложение! Сравнение коммутаторов серий 2960 и 3560
Сравнение коммутаторов серий 2960 и 3560 Родительское собрание онлайн
Родительское собрание онлайн Организация вычислений в электронных таблицах обработка числовой информации в электронных таблицах
Организация вычислений в электронных таблицах обработка числовой информации в электронных таблицах Единый портал государственных и муниципальных услуг
Единый портал государственных и муниципальных услуг Разработка сайта
Разработка сайта Բջջային հեռախոս. Համացանցից օգտվելու հնարավորություն
Բջջային հեռախոս. Համացանցից օգտվելու հնարավորություն Алгоритм. Использование LEGO-WеDо как исполнителя
Алгоритм. Использование LEGO-WеDо как исполнителя Цвет в компьютерной графики
Цвет в компьютерной графики Алгебра логики
Алгебра логики Массивы и указатели
Массивы и указатели Работа редактора с композицией медиатекста
Работа редактора с композицией медиатекста Автоматизированная информационная система результатов обучающихся в детской спортивной школе
Автоматизированная информационная система результатов обучающихся в детской спортивной школе Жизненный цикл программного обеспечения. Лекция №3
Жизненный цикл программного обеспечения. Лекция №3 Отчет о профессионально-творческой практике в Первичной профсоюзной организации
Отчет о профессионально-творческой практике в Первичной профсоюзной организации Поместите здесь ваш текст. Шаблон
Поместите здесь ваш текст. Шаблон Презентация на тему Интернет: да или нет
Презентация на тему Интернет: да или нет