Слайд 2Нечеткие числа
Взрослый человек. Почти взрослый. Точно взрослый
Высокий человек
Быстрая передача данных
Дорогая квартира (высокая

стоимость)
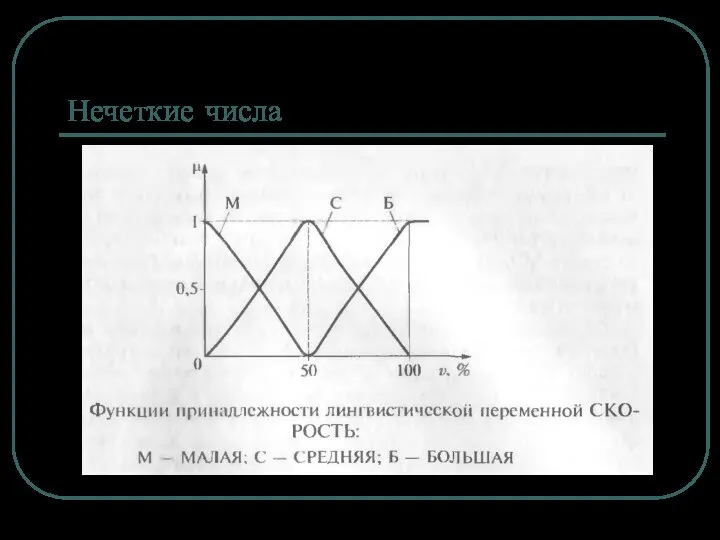
Высокая скорость
Надежный узел
Теплая / холодная / жаркая погода
Величина много больше, параметр значительно хуже
В задачах, где нет четкого определения / ответа
В задачах управления слабоструктурированными системами
В задачах построения АСУТП
Слайд 3Нечеткие числа
Лотфи Заде (теория нечетких множеств, теория нечеткой логики, теория мягких вычислений)
Нечеткое

множество - собрание элементов, которые могут принадлежать этому множеству со степенью от 0 до 1. Причем 0 обозначает абсолютную непринадлежность, а 1 - абсолютную принадлежность множеству.
Слайд 4Нечеткие числа
Функция принадлежности – субъективная мера принадлежности элемента x нечеткому множеству A.
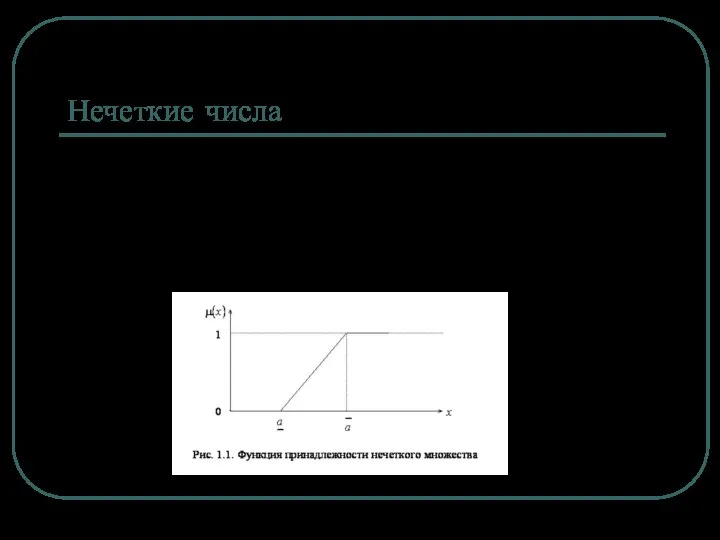
Слайд 5Нечеткие числа
Функция принадлежности – субъективная мера принадлежности элемента x нечеткому множеству A.
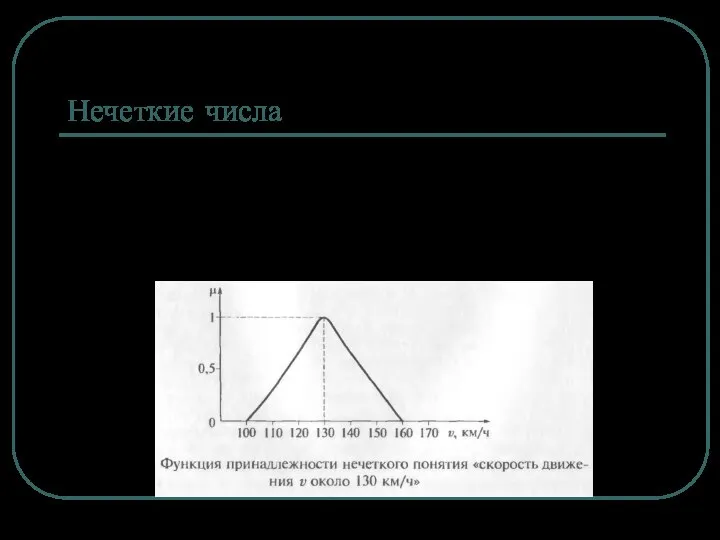
Слайд 7Нечеткие числа
Альфа-срезы (α-уровни)
Выпуклая функция принадлежности (трапециевидная, треугольная)
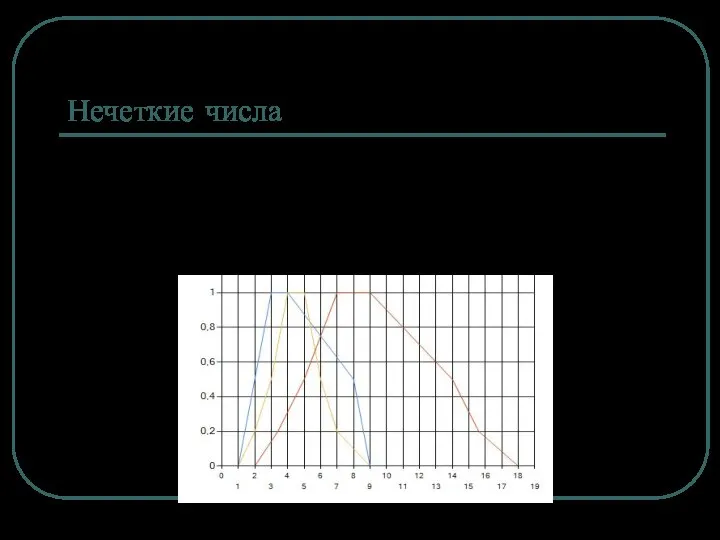
Слайд 8Нечеткие числа
! Треугольная и трапециевидная формы – частные случаи
Функция принадлежности в виде

α-срезов - аппроксимация
«Части» левой и правой сторон трапеции не обязательно симметричны
0 и 1 альфа-срезы задаются всегда
Слайд 9Нечеткие числа
Сложение нечетких чисел
складываются значения верхней границы одного множества со значениями верхней

границы другого множества для каждого α -среза, аналогично для нижних границ.
Слайд 11Нечеткие числа
Операция вычитания / разность двух нечетких чисел
из значения верхней границы одного

множества вычитается значение нижней границы другого множества и наоборот.
Слайд 13Нечеткие числа
Умножение
перемножаются значения верхней границы одного множества со значениями верхней границы другого

множества, аналогично для нижних границ
Слайд 15Нечеткие числа
Деление
значение верхней границы каждого среза одного множества делится на значение нижней

границы другого множества и наоборот
Слайд 17Нечеткие числа
Сравнение нечетких чисел
– количество α-срезов у каждого из чисел (могут быть

не равны)
Слайд 19Нечеткие числа
Если у двух чисел разное количество α-срезов или они заданы для

разных значений α-срезов, то для выполнения арифметических операций нужно найти дополнительные значения (для включения в формулу одинаковых α-срезов). Используется уравнение прямой, проходящей через две точки.
Слайд 20Нечеткие числа
При работе с трапициевидными или трегольными числами обязательно проверяется вложенность интервалов

(значений нижних и верхних границ для α-срезов) = выпуклость формы.
Слайд 21Нечеткие числа
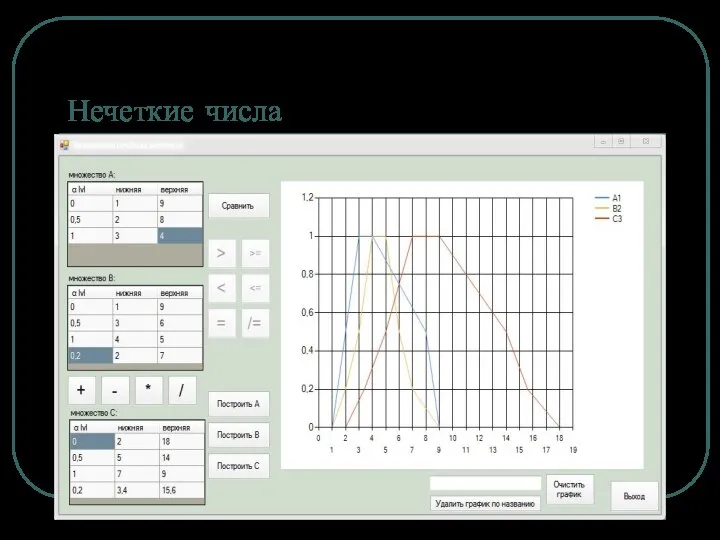
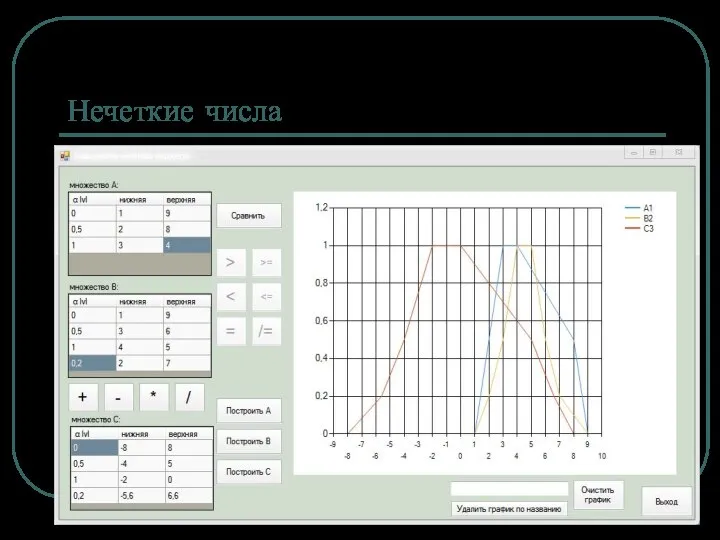
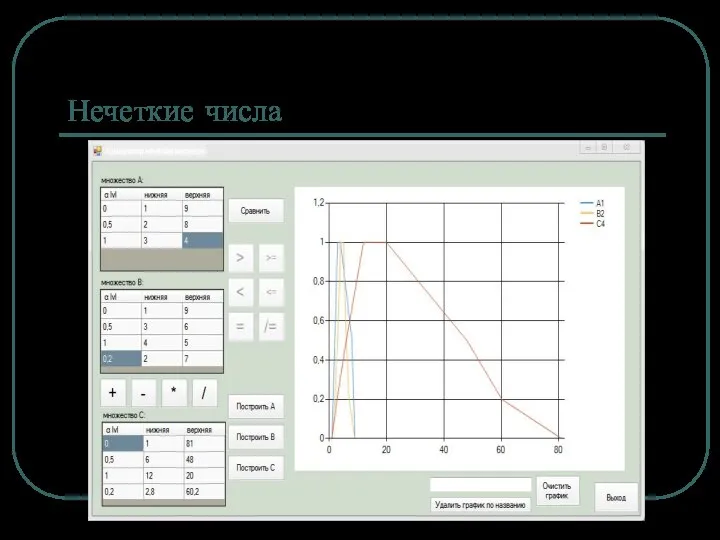
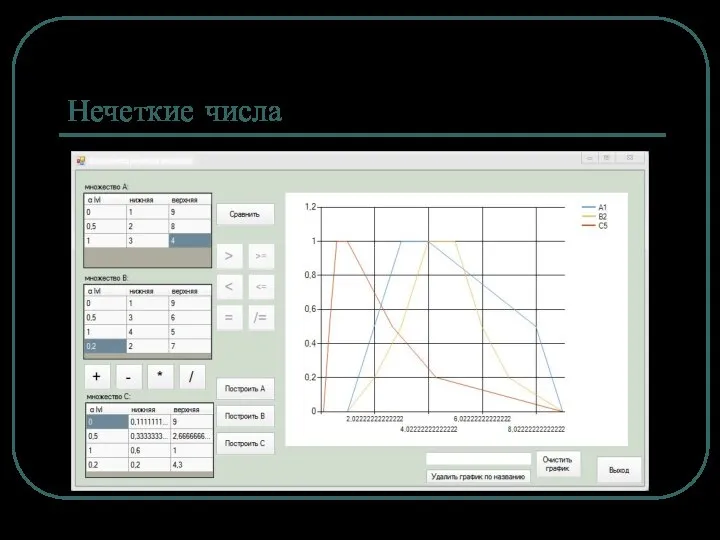
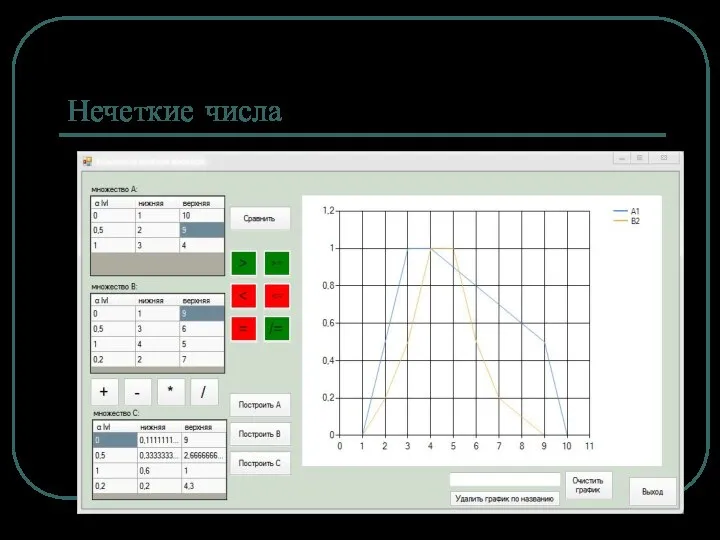
Пример в АСУТП
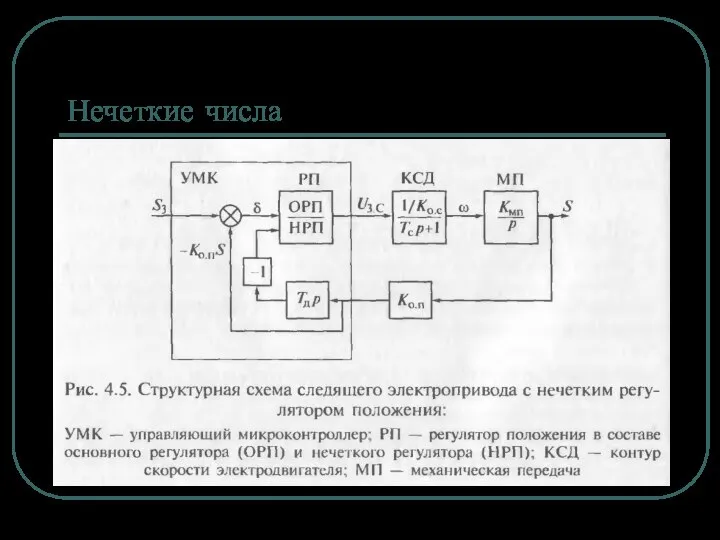
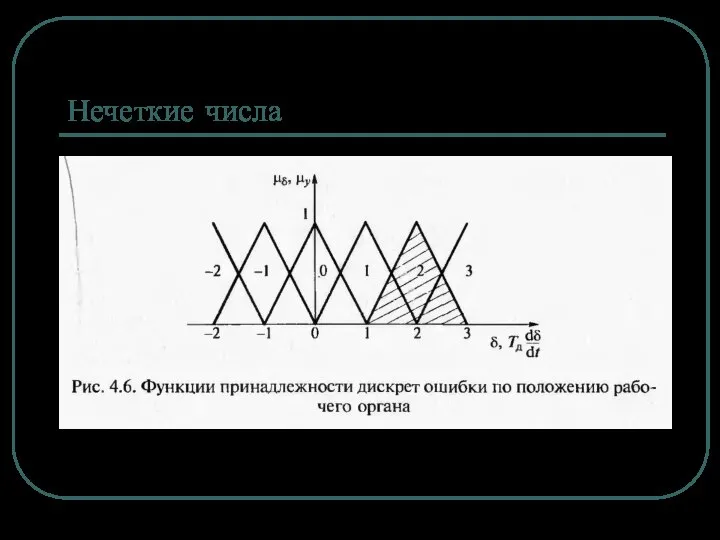
Синтез нечеткого регулятора положения
Цель – оптимизация режима позиционирования следящего

электропривода
















 9-1-4 (2)
9-1-4 (2) Журналистика 2000-х годов
Журналистика 2000-х годов Что такое гиперссылка и как она работает?
Что такое гиперссылка и как она работает? Игра Roguemings - старые-добрые лемминги в новых условиях
Игра Roguemings - старые-добрые лемминги в новых условиях Классы без стен или коммуникативные методики западной школы
Классы без стен или коммуникативные методики западной школы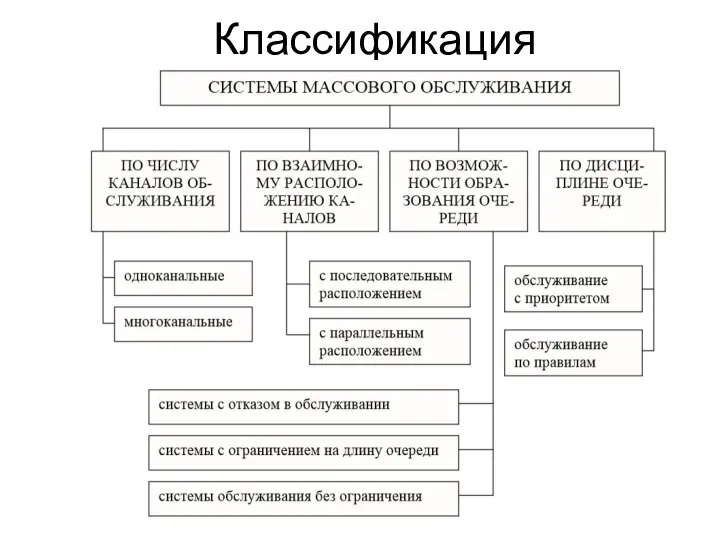 Классификация системы массового обслуживания
Классификация системы массового обслуживания Качество программного обеспечения
Качество программного обеспечения New Trenitalia APP. Incremental innovation: seen in the social network market
New Trenitalia APP. Incremental innovation: seen in the social network market Верстка_web_страниц__Селекторы-1
Верстка_web_страниц__Селекторы-1 Прикладное программирование на PHP
Прикладное программирование на PHP День защиты информации
День защиты информации Software. Operating system
Software. Operating system Измерение информации
Измерение информации Технологическая архитектура предприятия
Технологическая архитектура предприятия База данных Visual FoxPro 6.0 (основные понятия и инструментальные средства среды разработки)
База данных Visual FoxPro 6.0 (основные понятия и инструментальные средства среды разработки) Производные типы данных: массивы
Производные типы данных: массивы Системное программное обеспечение
Системное программное обеспечение Технологии реализации интерфейсов
Технологии реализации интерфейсов Гуру обработки
Гуру обработки Три шага для активации автоматического отслеживания заказов партнеров
Три шага для активации автоматического отслеживания заказов партнеров Каскадные таблицы стилей CSS
Каскадные таблицы стилей CSS Презентация на тему Передача информации
Презентация на тему Передача информации  Функции Счётесли и Счётеслимн
Функции Счётесли и Счётеслимн Бинарные (фиктивные) переменные
Бинарные (фиктивные) переменные Чистый код. Приемы написания красивого и понятного кода
Чистый код. Приемы написания красивого и понятного кода Объектно-ориентированные технологии программирования и стандарты проектирования
Объектно-ориентированные технологии программирования и стандарты проектирования Сравнительный анализ дизайна интернет-сайтов
Сравнительный анализ дизайна интернет-сайтов Risuemdoma.com
Risuemdoma.com