Neural Networks

Pachshenko
Galina Nikolaevna
Associate Professor of Information System Department,
Candidate of Technical Science

Week 4
Lecture 4

Topics
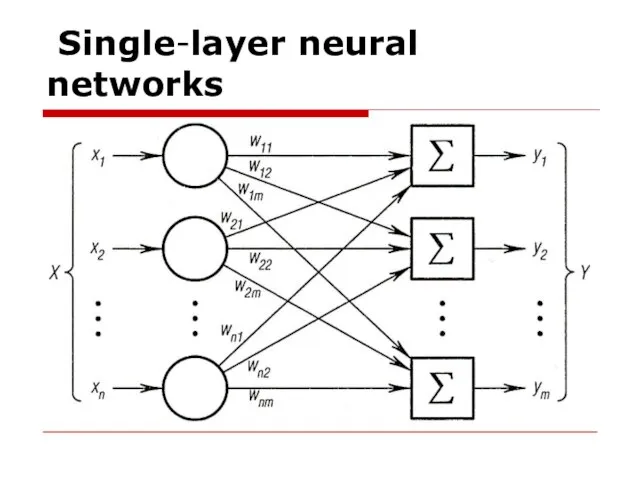
Single-layer neural networks
Multi-layer neural networks
Single perceptron
Multi-layer perceptron
Hebbian Learning Rule
Back propagation
Delta-rule
Weight adjustment
Cost Function
Сlassification (Independent Work)

Single-layer neural networks

Multi-layer neural networks

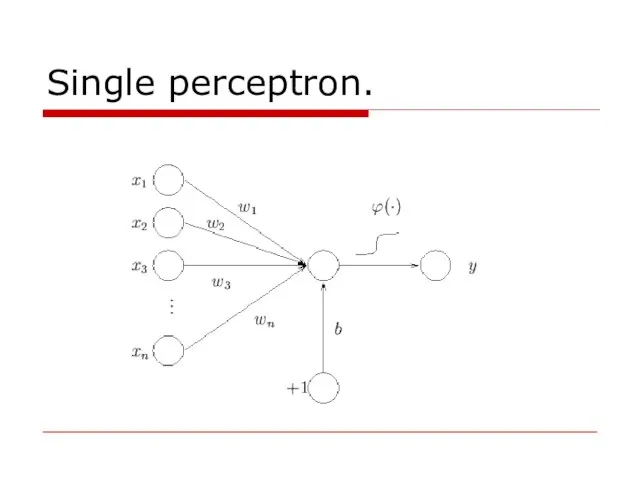
Single perceptron
The perceptron computes a single output from multiple real-valued inputs by forming a linear combination according to its input weights and then possibly putting the output through activation function.

Single perceptron.
Mathematically this can be written as

Single perceptron.

Task 1:
Write a program that finds output of a single perceptron.
Note:
Use bias. The bias shifts the decision boundary away from the origin and does not depend on any input value.

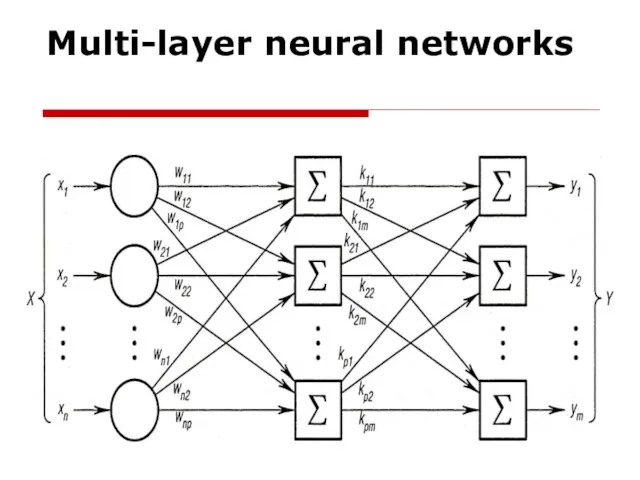
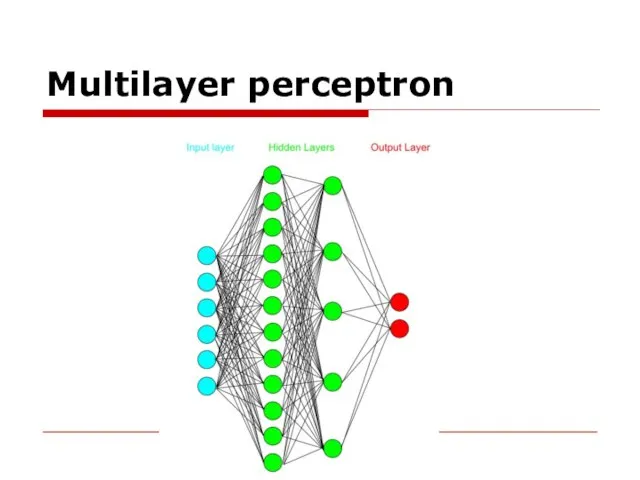
Multilayer perceptron
A multilayer perceptron (MLP) is a class of feedforward artificial neural network.

Multilayer perceptron

Structure
• nodes that are no target of any connection are called input neurons.

• nodes that are no source of any connection are called output neurons.
A MLP can have more than one output neuron.
The number of output neurons depends on the way the target values (desired values) of the training patterns are described.

• all nodes that are neither input neurons nor output neurons are called hidden neurons.
• all neurons can be organized in layers, with the set of input layers being the first layer.

The original Rosenblatt's perceptron used a Heaviside step function as the activation function.

Nowadays, in multilayer networks, the activation function is often chosen to be the sigmoid function

or the hyperbolic tangent

They are related by

These functions are used because they are mathematically convenient.

An MLP consists of at least three layers of nodes.
Except for the input nodes, each node is a neuron that uses a nonlinear activation function.

MLP utilizes a supervised learning technique called backpropagation for training.

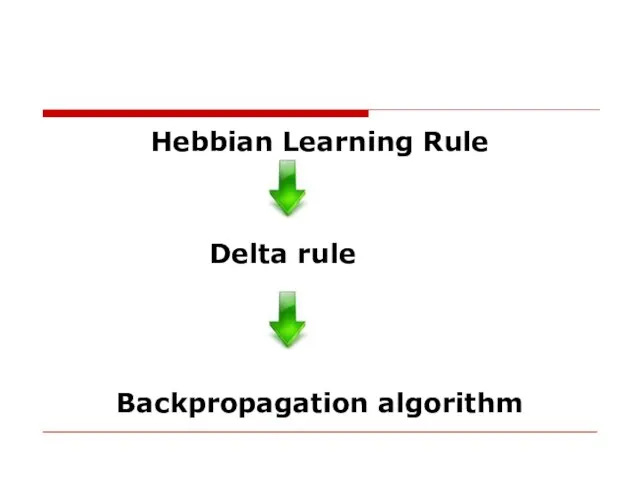
Hebbian Learning Rule
Delta rule
Backpropagation algorithm

Hebbian Learning Rule
(Hebb's rule)
The Hebbian Learning Rule (1949)
is a learning rule that specifies how much the weight of the connection between two units should be increased or decreased in proportion to the product of their activation.

Hebbian Learning Rule
(Hebb's rule)

Delta rule
(proposed in 1960)

The backpropagation algorithm was originally introduced in the 1970s, but its importance wasn't fully appreciated until a famous 1986 paper by David Rumelhart, Geoffrey Hinton, and Ronald Williams.

That paper describes several neural networks where backpropagation works far faster than earlier approaches to learning, making it possible to use neural nets to solve problems which had previously been insoluble.

Supervised Backpropagation – The mechanism of backward error transmission (delta learning rule) is used to modify the weights of the internal (hidden) and output layers

Back propagation
The back propagation learning algorithm uses the delta-rule.
What this does is that it computes the deltas, (local gradients) of each neuron starting from the output neurons and going backwards until it reaches the input layer.

The delta rule is derived by attempting to minimize the error in the output of the neural network through gradient descent.

To compute the deltas of the output neurons though we first have to get the error of each output neuron.

That’s pretty simple, since the multi-layer perceptron is a supervised training network so the error is the difference between the network’s output and the desired output.
ej(n) = dj(n) – oj(n)
where e(n) is the error vector, d(n) is the desired output vector and o(n) is the actual output vector.

Now to compute the deltas:
deltaj(L)(n) = ej(L)(n) * f'(uj(L)(n)) ,
for neuron j in the output layer L
where f'(uj(L)(n)) is the derivative of the value of the jth neuron of layer L

The same formula:

Weight adjustment
Having calculated the deltas for all the neurons we are now ready for the third and final pass of the network, this time to adjust the weights according to the generalized delta rule:

Weight adjustment

For

Note: For sigmoid activation function
Derivative of the function:
S'(x) = S(x)*(1 - S(x))

Cost Function
We need a function that will minimize the parameters over our dataset. One common function that is often used is mean squared error

Squared Error: which we can minimize using gradient descent
A cost function is something you want to minimize. For example, your cost function might be the sum of squared errors over your training set. Gradient descent is a method for finding the minimum of a function of multiple variables. So you can use gradient descent to minimize your cost function.

Back-propagation is a gradient descent over the entire networks weight vectors.
In practice, it often works well and can run multiple times. It minimizes error over all training samples.

Task 2:
Write a program that can update weights of neural network using backpropagation.