Содержание
- 2. Введение Современный человек в повседневной жизни постоянно сталкивается с числами и цифрами - они с нами
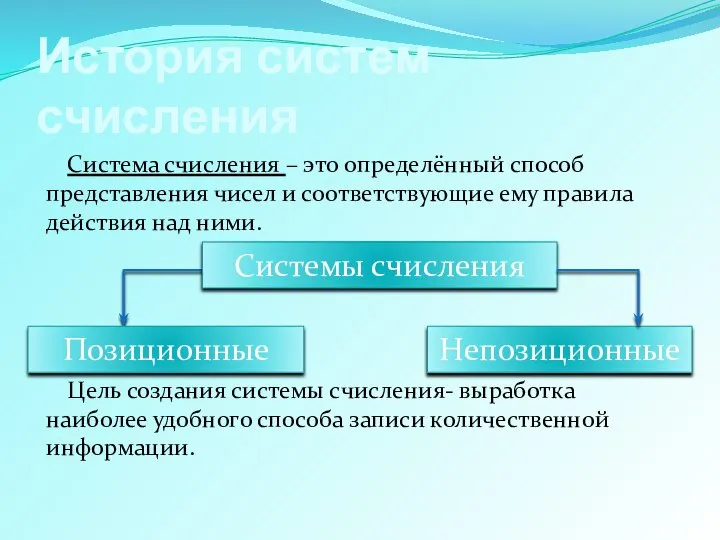
- 3. Система счисления – это определённый способ представления чисел и соответствующие ему правила действия над ними. Цель
- 4. Древние системы счисления: Единичная система Древнегреческая нумерация Славянская нумерация Римская нумерация
- 5. Позиционные и непозиционные системы счисления
- 6. Запись числа в позиционной системе счисления Любое целое число в позиционной системе можно записать в форме
- 7. Примеры позиционных систем счисления:
- 8. ИСТОРИЯ ДВОИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ Двоичная система счисления была придумана математиками и философами ещё до появления компьютеров
- 9. Двоичная система счисления Двоичная система счисления (бинарная система счисления, binary) — позиционная система счисления с основанием
- 10. Сложение, вычитание, умножение и деление в двоичной системе счисления
- 11. Двоичное кодирование в компьютере В конце ХХ века, века компьютеризации, человечество пользуется двоичной системой ежедневно, так
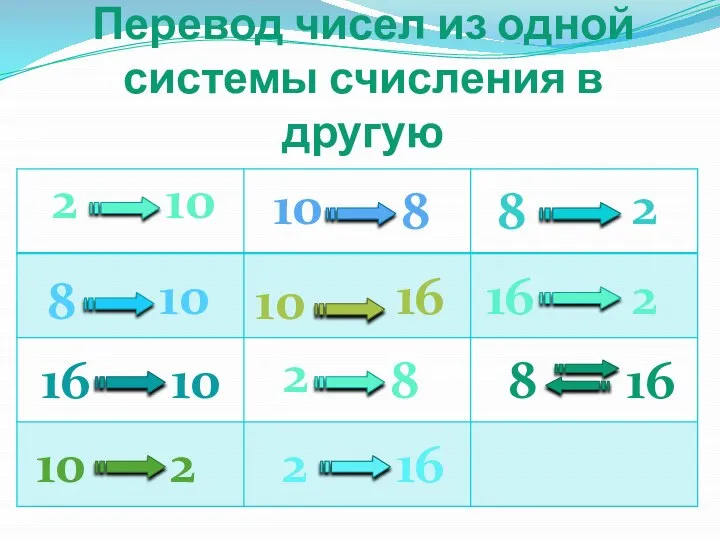
- 12. Перевод чисел из одной системы счисления в другую 8 16
- 13. Заключение Высшим достижением древней арифметики является открытие позиционного принципа представления чисел. Нужно признать важность не только
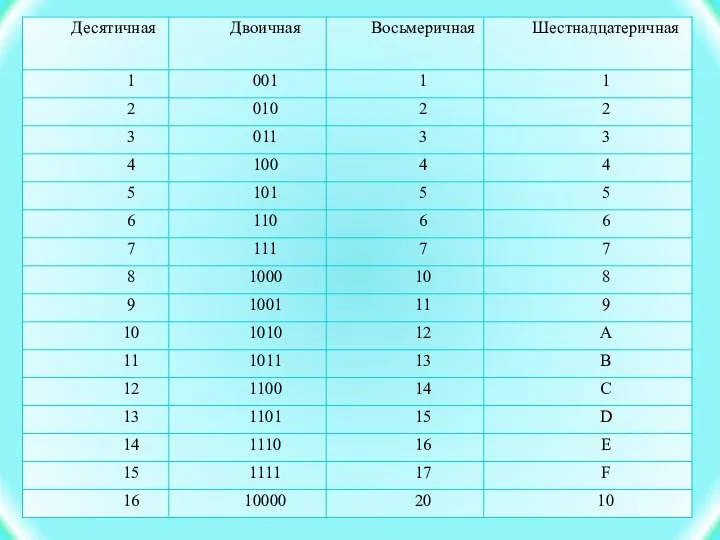
- 15. Перевод двоичного числа в десятичное Для перевода двоичного числа в десятичное необходимо его записать в виде
- 16. ПЕРЕВОД ВОСЬМЕРИЧНОГО ЧИСЛА В ДЕСЯТИЧНОЕ Для перевода восьмеричного числа в десятичное необходимо его записать в виде
- 17. Перевод шестнадцатеричного числа в десятичное Для перевода шестнадцатеричного числа в десятичное необходимо его записать в виде
- 18. Перевод десятичного числа в двоичную систему Для перевода десятичного числа в двоичную систему его необходимо последовательно
- 19. Перевод десятичного числа в восьмеричную систему Для перевода десятичного числа в восьмеричную систему его необходимо последовательно
- 20. Перевод десятичного числа в шестнадцатеричную систему Для перевода десятичного числа в шестнадцатеричную систему его необходимо последовательно
- 21. ПЕРЕВОД ЧИСЕЛ ИЗ ДВОИЧНОЙ СИСТЕМЫ В ВОСЬМЕРИЧНУЮ Чтобы перевести число из двоичной системы в восьмеричную, его
- 22. Перевод из двоичной системы в шестнадцатеричную Чтобы перевести число из двоичной системы в шестнадцатеричную, его нужно
- 23. Перевод восьмеричного числа в двоичное Для перевода восьмеричного числа в двоичное необходимо каждую цифру заменить эквивалентной
- 24. Перевод шестнадцатеричного числа в двоичное Для перевода шестнадцатеричного числа в двоичное необходимо каждую цифру заменить эквивалентной
- 25. Перевод из восьмеричной системы счисления в шестнадцатеричную и обратно При переходе из восьмеричной системы счисления в
- 26. Единичная система В древние времена, когда появилась потребность в записи чисел, количество предметов, изображалось нанесением черточек
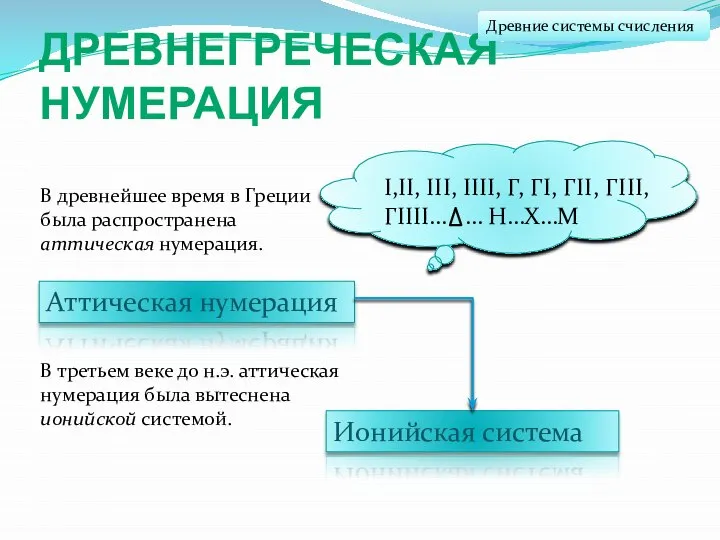
- 27. ДРЕВНЕГРЕЧЕСКАЯ НУМЕРАЦИЯ Аттическая нумерация Ионийская система В третьем веке до н.э. аттическая нумерация была вытеснена ионийской
- 28. СЛАВЯНСКАЯ НУМЕРАЦИЯ В России славянская нумерация сохранилась до конца XVII века. Южные и восточные славянские народы
- 29. Римская нумерация Древние римляне пользовались нумерацией, которая сохраняется до настоящего времени под именем «римской нумерации». Мы
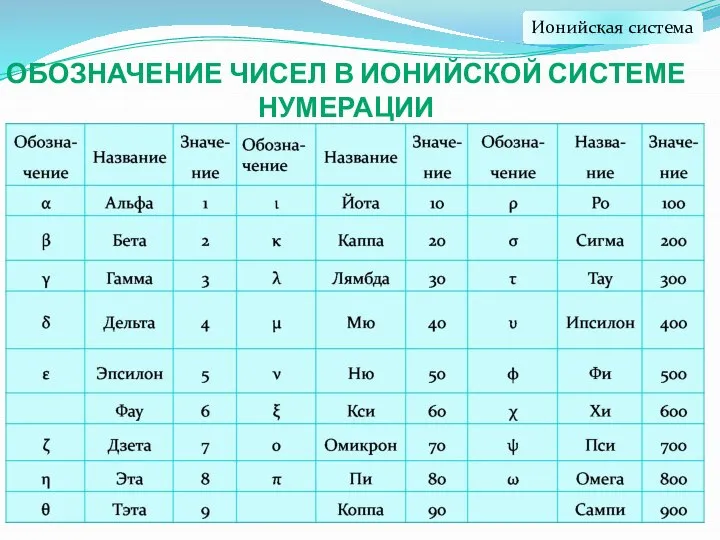
- 30. Ионийская система ОБОЗНАЧЕНИЕ ЧИСЕЛ В ИОНИЙСКОЙ СИСТЕМЕ НУМЕРАЦИИ
- 32. Скачать презентацию
























 Каналы размещения контента
Каналы размещения контента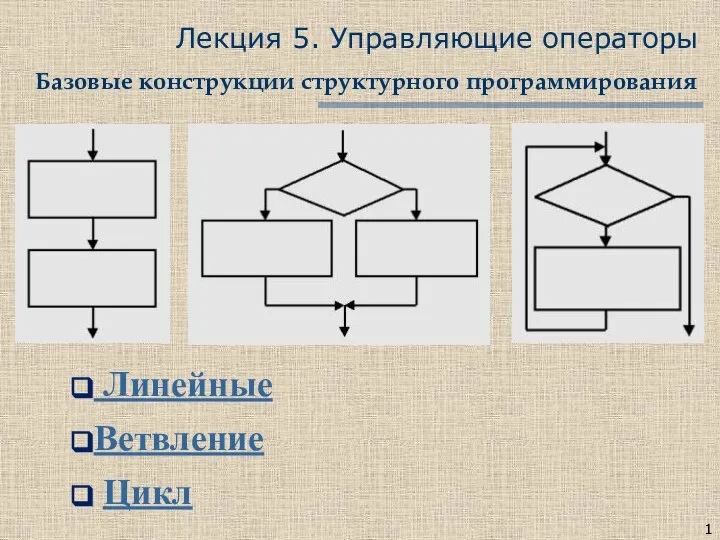 Управляющие операторы. Базовые конструкции структурного программирования. Лекция 5
Управляющие операторы. Базовые конструкции структурного программирования. Лекция 5 Электронный обучающий комплекс по компьютерному моделированию динамики механической системы
Электронный обучающий комплекс по компьютерному моделированию динамики механической системы Тенденции развития программного обеспечения
Тенденции развития программного обеспечения Хакатон
Хакатон Программа Movie Maker. Информатика и ИКТ. 6 класс
Программа Movie Maker. Информатика и ИКТ. 6 класс Азы пользования компьютером для пенсионеров
Азы пользования компьютером для пенсионеров Автоматизация учета расчетов с персоналом по оплате труда
Автоматизация учета расчетов с персоналом по оплате труда Электронные презентации
Электронные презентации Устройства обработки информации. Процессоры, платы
Устройства обработки информации. Процессоры, платы Інструкція по користуванню терміналами. Банки
Інструкція по користуванню терміналами. Банки Общие сведения о современном ПК
Общие сведения о современном ПК Операционная система (ОС)
Операционная система (ОС) Системы счисления. Математические основы информатики
Системы счисления. Математические основы информатики JavaScript. Dev tools
JavaScript. Dev tools Этапы развития информационных технологий
Этапы развития информационных технологий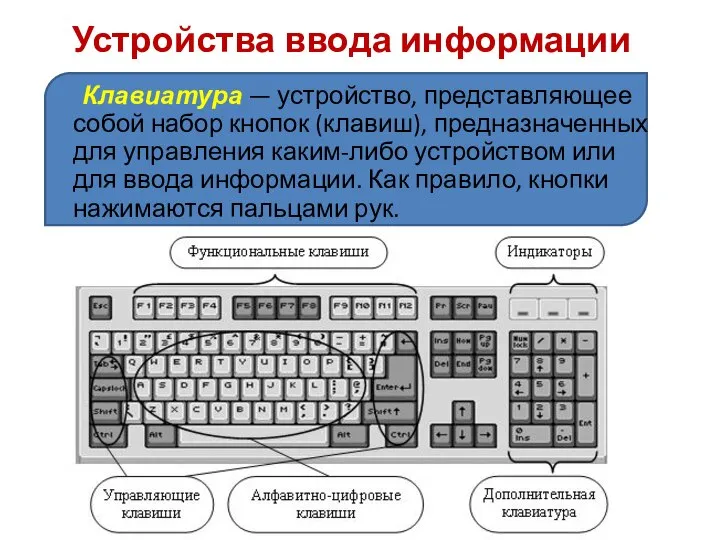 Устройства ввода информации
Устройства ввода информации Понятие операционной системы
Понятие операционной системы Barbershop - Old Schol Новый промо-сайт. Микроанимация элементов Загрузка страниц Переходы Эффекты
Barbershop - Old Schol Новый промо-сайт. Микроанимация элементов Загрузка страниц Переходы Эффекты Как запланировать онлайн лекцию
Как запланировать онлайн лекцию 422196
422196 Вводная информация по работе с сервисным порталом TPV
Вводная информация по работе с сервисным порталом TPV Лекция 4. Курсовая работа по дисциплине Основы конструирования программ (2 семестр)
Лекция 4. Курсовая работа по дисциплине Основы конструирования программ (2 семестр) Защита информации
Защита информации Тармаклануны Паскаль телендә программалау
Тармаклануны Паскаль телендә программалау Элементы системы управления базами данных Access
Элементы системы управления базами данных Access Обзор сервиса
Обзор сервиса Локальные компьютерные сети (КС). Особенности компьютерных сетей
Локальные компьютерные сети (КС). Особенности компьютерных сетей