Содержание
- 2. Сортировка на линейных сетях Если число процессоров равно числу сортируемых значений , то сортировку можно осуществить,
- 3. Сортировка на линейных сетях A.
- 4. Сортировка на линейных сетях B.
- 5. Сортировка на линейных сетях В.
- 6. Характеристики : В общем случае алгоритм выполняет 2 * (N — 1) + 1 (т.е. O(N)),
- 7. Четно-нечетная сортировка перестановками В четно нечетной сортировке сравниваются соседние значения и при необходимости переставляются.
- 8. Четно-нечетная сортировка перестановками Пример для списка : 15, 18, 13, 12, 17, 11, 19, 16, 14
- 9. Четно-нечетная сортировка перестановками Все сравнения происходят параллельно, поэтому всякий проход цикла выполняет два сравнения и общее
- 10. Другие алгоритмы Если у нас список без повторений, то мы можем отсортировать его с помощью подсчета.
- 12. Скачать презентацию









 Современные компьютерные технологии в деятельности государственных служащих
Современные компьютерные технологии в деятельности государственных служащих Drive Ahead Valentine’s Day Event
Drive Ahead Valentine’s Day Event Безопасный интернет
Безопасный интернет Приобретение, разработка и эксплуатация информационных систем. Лекция 8
Приобретение, разработка и эксплуатация информационных систем. Лекция 8 Циклы, массивы, таблицы
Циклы, массивы, таблицы Компьютерная безграмотность
Компьютерная безграмотность Как регистрировать ребёнка
Как регистрировать ребёнка Гибридные информационные системы в промышленности
Гибридные информационные системы в промышленности Рубрики Вконтакте. Откуда взять идею?
Рубрики Вконтакте. Откуда взять идею? Цикл получения информации
Цикл получения информации БАРС Web - Электронная школа
БАРС Web - Электронная школа Центральный процессор
Центральный процессор Типы данных. Переменные в С#
Типы данных. Переменные в С# Формы оператора TKР
Формы оператора TKР Создание меню в ЛИСПе
Создание меню в ЛИСПе Техника безопасности и правила поведения при работе в компьютерном классе
Техника безопасности и правила поведения при работе в компьютерном классе Оформление проекта с использованием MS Office
Оформление проекта с использованием MS Office Minecraft Education. Язык программирования
Minecraft Education. Язык программирования Кодирование информации
Кодирование информации 12. основные принципы построения скс
12. основные принципы построения скс Хлеб блокадного Ленинграда
Хлеб блокадного Ленинграда Электронная почта
Электронная почта Этапы прохождения. Играть
Этапы прохождения. Играть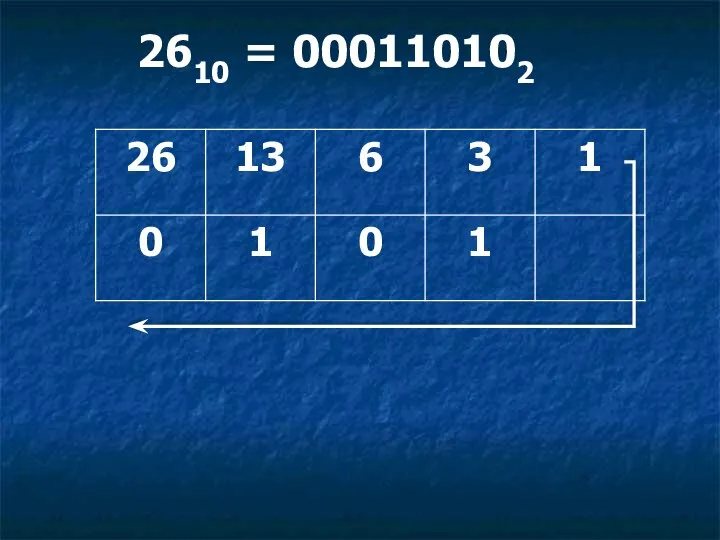 Кодирование графической информации. Флажковая азбука
Кодирование графической информации. Флажковая азбука Векторная графика. Состав и области применения
Векторная графика. Состав и области применения Описание настройки программного отраслевой направленности
Описание настройки программного отраслевой направленности Проектирование и разработка программного средства реализации онлайн - сервиса управления личным кабинетом
Проектирование и разработка программного средства реализации онлайн - сервиса управления личным кабинетом Нотация EPC
Нотация EPC