Понятие информации в теории Шеннона

Случайное событие – означает отсутствие полной уверенности в его наступлении.
Пусть опыт имеет n равновероятных исходов.
Определение. Функция f(n) - мера неопределенности опыта.
Мера неопределенности является функцией числа исходов f(n).

f(1) = 0, если n = 1 исход опыта не является случайным и неопределенность отсутствует;
f(n) возрастает с ростом n,
чем больше n, тем более затруднительным становится предсказание результата опыта;
Свойства функции f(n)

Пусть α и β независимые опыты.
nα, nβ - число равновероятных исходов.
Рассмотрим сложный опыт, который состоит в одновременном выполнении опытов
α и β.
Число возможных его исходов равно:
nα ∙ nβ,
причем, все они равновероятны.

f(nα ∙ nβ) - мера неопределенности сложного опыта.
α и β – независимы, т.е. в сложном опыте они не влияют друг на друга.
Следовательно,
f(nα ∙ nβ)= f(nα) + f(nβ) (3)
т.е. мера неопределенности аддитивна.

f(1) = 0
f(n) возрастает с ростом n
f(nα ∙ nβ)= f(nα) + f(nβ)
Этим свойствам удовлетворяет функция: log(n)
можно доказать, что она единственная из всех существующих классов функций.
f(n)= log(n) (4)
мера неопределенности опыта, имеющего n равновероятных исходов.

Выбор основания логарифма значения не имеет.
переход к другому основанию состоит во введении одинакового для обеих частей выражения постоянного множителя
logbа

Удобно, основание 2.
За единицу измерения принимается неопределенность, содержащаяся в опыте, имеющем лишь два равновероятных исхода,
ИСТИНА (True) и ЛОЖЬ (False).
f(2)=log22=1 бит.
Определение. Единица измерения неопределенности при двух возможных равновероятных исходах опыта называется бит.
Название бит происходит от английского binary digit, «двоичный разряд» или «двоичная единица».

Определение. Мера неопределенности опыта, имеющего n равновероятных исходов равна
f(n)=log2(n). (4.1)
Эта величина – энтропия, обозначается Н.

Рассмотрим опыт с n равновероятными исходами.
Неопределенность, вносимую одним исходом?
где р =1/n - вероятность любого из отдельных исходов.

Пусть исходы неравновероятны,
р(А1) и р(А2) – вероятности исходов.
Если опыт α имеет n неравновероятных исходов А1, А2... Аn, тогда:

Используя формулу для среднего значения дискретных случайных величин:
А(α) - обозначает исходы, возможные в опыте α.

Определение. Энтропия является мерой неопределенности опыта, в котором проявляются случайные события, и равна средней неопределенности всех возможных его исходов.

ПРИМЕР
Имеются два ящика, в каждом из которых по 12 шаров. В первом - 3 белых, 3 черных и 6 красных; во втором - каждого цвета по 4. Опыты состоят в вытаскивании по одному шару из каждого ящика. Что можно сказать относительно неопределенностей исходов этих опытов?
Решаем :-).

Нβ > Нα, т.е. неопределенность результата в опыте β выше и, следовательно, предсказать его можно с меньшей долей уверенности, чем результат опыта α.

Свойства энтропии
1) Н > 0.
Н = 0 в двух случаях:
(а) если p(Aj) = 1; т.е. один из исходов является достоверным (и общий итог опыта перестает быть случайным);
(b) все р(Аi) = 0, т.е. никакие из рассматриваемых исходов опыта невозможны.

2) Для двух независимых опытов α и β
Энтропия сложного опыта, состоящего из нескольких независимых, равна сумме энтропии отдельных опытов.

3) При прочих равных условиях наибольшую энтропию имеет опыт с равновероятными исходами.

Условная энтропия
Найдем энтропию сложного опыта α ^ β (опыты не являются независимыми, на исход β оказывает влияние результат опыта α).
Пример, если в ящике два разноцветных шара и α – извлечение первого, а β - второго, тогда α полностью снимает неопределенность сложного опыта α ^ β,
т.е. Н(α ^ β) = H(α),
a не сумме энтропий.

Подставим в (7)

В первом слагаемом индекс j имеется только у B; изменив порядок суммирования, получим члены вида:

Свойства условной энтропии
1. Условная энтропия является величиной неотрицательной.
Hα(β) = 0, если любой исход α полностью определяет исход β
2. Если α и β независимы, то Нα(β) = Н(β), причем это оказывается наибольшим значением условной энтропии, т.е. условная энтропия не превосходит безусловную.

Пример 2.2.
В ящике имеются 2 белых шара и 4 черных. Из ящика извлекают последовательно два шара без возврата. Найти энтропию, связанную с первым и вторым извлечениями, а также энтропию обоих извлечений.

Задача 2.3.
Имеется три тела с одинаковыми внешними размерами, но с разными массами х1, х2 и х3. Необходимо определить энтропию, связанную с нахождением наиболее тяжелого из них, если сравнивать веса тел можно только попарно.

2.2. Энтропия и информация
Определение. I - информацией относительно опыта β, содержащейся в опыте α
I(α,β)=H (β)-Hβ(α)

Следствие 1. Единицы измерения количество информации – бит.
Следствие 2. Пусть опыт α = β, тогда
Нβ(β) = 0 (свойство усл. энтропии)
I(β,β) = Н(β).
Определение. Энтропия опыта равна той информации, которую получаем в результате его осуществления.

Свойств информации:
1. /(α, β) ≥ 0, причем /(α, β) = 0 тогда и только тогда, когда опыты α и β независимы.
2. /(α, β) = /(β, α), т.е. информация симметрична относительно последовательности опытов.
3. Информация опыта равна:

Пример 2.4. Какое количество информации требуется, чтобы узнать исход броска монеты?
Пример 2.5. Виктор Сергеевич задумал «оценку» (целое число в интервале от 2 до 5). Опыт состоит в угадывании этого числа. На вопросы В.С. отвечает лишь «Да» или «Нет». Какое количество информации должны получить, чтобы узнать задуманную оценку? Как правильно построить процесс угадывания?

Количество информации численно равно числу вопросов с равновероятными бинарными вариантами ответов, которые необходимо задать, чтобы полностью снять неопределенность задачи.
Если все n исходов равновероятны

Формула Хартли (1928).
30.11.1888 - 1.05.1970 (81). США

Cвязывает количество равновероятных состояний (n) и (/), что любое из этих состояний реализовалось.
Частным случаем применения формулы Хартли является ситуация, когда n = 2^k.
k равно количеству вопросов с бинарными равновероятными ответами, которые определяют количество информации.

Пример 2.6 В.С. случайным образом вынимает карта из колоды в 32 карты. Какое количество информации требуется, чтобы угадать, что это за карта? Как построить угадывание?
Пример 2.7 В некоторой местности имеются две близкорасположенные деревни: А и В. Жители А всегда говорят правду, а жители В - всегда лгут. Жители обеих деревень любят ходить друг к другу в гости, поэтому в каждой из деревень можно встретить жителя соседней деревни. Путешественник, оказался в одной из двух деревень и, заговорив с первым встречным, захотел выяснить, в какой деревне он находится и откуда его собеседник. Какое минимальное количество вопросов с бинарными ответами требуется задать путешественнику?

Выводы
1. Выражение
является статистическим определением понятия «информация», поскольку в него входят вероятности возможных исходов опыта.
Операционное определение новой величины, т.е. устанавливается процедура (способ) ее измерения.

2. Если начальная энтропия опыта Н1, а в результате сообщения информации / энтропия становится равной Н2 (Н1 ≥ Н2), то
т.е. информация равна убыли энтропии.

Если изначально равновероятных исходов было n1, а в результате передачи информации I неопределенность уменьшилась, и число исходов стало n2 то

Определение. Информация - это содержание сообщения, понижающего неопределенность некоторого опыта с неоднозначным исходом; убыль связанной с ним энтропии является количественной мерой информации.
В случае равновероятных исходов информация равна логарифму отношения числа возможных исходов до и после (получения сообщения).

3. Аддитивность информации.
Пусть IА = log2nA - первого опыта,
IB = log2nB - второго опыта,
второй выбор никак не связан с первым.
При объединении число возможных состояний (элементов) будет
n = nА ∙ nB и потребуется количество информации:

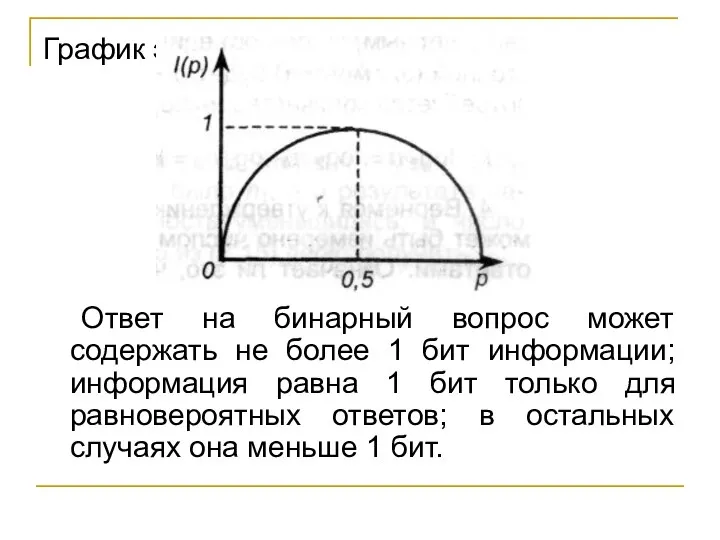
4. Рассмотрим опыт, реализующийся посредством двух случайных событий; если эти события равновероятны,
р1 = р2 = 1/2, и I = 1 бит, как следует из формулы Хартли.
Если их вероятности различны: р1 = р, то, p2 = 1 - р, и следовательно:

График этой функции
Ответ на бинарный вопрос может содержать не более 1 бит информации; информация равна 1 бит только для равновероятных ответов; в остальных случаях она меньше 1 бит.

Пример 2.8. При угадывании результата броска игральной кости задается вопрос «Выпало 6?». Какое количество информации содержит ответ?

На бытовом уровне, «информация» отождествляется с «информированностью», т.е. человеческим знанием.
В «теории информации» информация является мерой нашего незнания чего-либо (но что в принципе может произойти); как только это происходит и узнаем результат, информация, связанная с данным событием, исчезает. Состоявшееся событие не несет информации, поскольку пропадает его неопределенность (энтропия становится равной нулю), и I = 0.

Глава 3. Кодирование символьной информации
3.1. Постановка задачи кодирования. Первая теорема Шеннона
3.2. Способы построения двоичных кодов

3.1. Постановка задачи кодирования. Первая теорема Шеннона
Код
(1) правило, описывающее соответствие знаков или их сочетаний первичного алфавита знакам или их сочетаниям вторичного алфавита.
(2) набор знаков вторичного алфавита, используемый для представления знаков или их сочетаний первичного алфавита.
Кодирование - перевод информации, представленной сообщением в первичном алфавите, в последовательность кодов.

Декодирование - операция, обратная кодированию, т.е. восстановление информации в первичном алфавите по полученной последовательности кодов.
Кодер - устройство, обеспечивающее выполнение операции кодирования.
Декодер - устройство, производящее декодирование.
Операции кодирования и декодирования называются обратимыми, если их последовательное применение обеспечивает возврат к исходной информации без каких-либо ее потерь.

Источник представляет информацию в форме дискретного сообщения, используя для этого алфавит - первичным.
Далее сообщение попадает в устройство, преобразующее и представляющее его в другом алфавите - вторичным.

Математическая постановка задачи кодировании. Пусть первичный алфавит
А состоит из N знаков со средней информацией на знак I(A),
вторичный алфавит B - из М знаков со средней информацией на знак I(B).
Пусть исходное сообщение, содержит n знаков, а закодированное сообщение - т знаков.
Если исходное сообщение содержит Ist(A) информации, а закодированное - Ifin(B), то условие обратимости кодирования:

Операция обратимого кодирования может увеличить количество информации в сообщении, но не может его уменьшить.

т/n - характеризует среднее число знаков вторичного алфавита, которое приходится использовать для кодирования одного знака первичного алфавита.
Это - длина кода - К(А,В).

Обычно N > М и I(А) > I(В), откуда К(А,В) > 1, т.е. один знак первичного алфавита представляется несколькими знаками вторичного.
Способов построения кодов при фиксированных алфавитах А и В множество, возникает проблема выбора (или построения) наилучшего варианта - оптимального кода.

Минимально возможным значением средней длины кода
устанавливающее нижний предел длины кода.

Первая теорема Шеннона (основная теорема о кодировании при отсутствии помех).
1. При отсутствии помех всегда возможен такой вариант кодирования сообщения, при котором среднее число знаков кода, приходящихся на один знак первичного алфавита, будет сколь угодно близко к отношению средних информации на знак первичного и вторичного алфавитов.

Смысл теоремы: теорема открывает принципиальную возможность оптимального кодирования, т.е. построения кода со средней длиной Кmin(А,В).

Два пути сокращения Кmin(А,В):
1. уменьшение числителя - если при кодировании учесть различие частот появления разных знаков в сообщении, корреляции (двухбуквенные, трехбуквенные и т.д.)
2. увеличение знаменателя - найти такой способ кодирования, при котором появление знаков вторичного алфавита было бы равновероятным, т.е.
I(B) = log2 M.

Для первого приближения
Относительная избыточность кода:

Данная величина показывает, насколько операция кодирования увеличила длину исходного сообщения.
Q(A,B) → 0 при К(А,В) → Кmin(А,В).
Теорема Шеннона:
2. При отсутствии помех всегда возможен такой вариант кодирования сообщения, при котором избыточность кода будет сколь угодно близкой к нулю.

Наиболее важной для практики оказывается ситуация, когда М = 2, т.е. для представления кодов в линии связи используется лишь два типа сигналов.
Тогда log2(M) = 1, и
3. При отсутствии помех средняя длина двоичного кода может быть сколь угодно близкой к средней информации, приходящейся на знак первичного алфавита.

3.2. Способы построения двоичных кодов

Возможны следующие особенности вторичного алфавита:
элементарные сигналы (0 и 1) могут иметь одинаковые длительности (to=t1) или разные (to≠t1);
длина кода может быть одинаковой для всех знаков первичного алфавита – равномерный код
коды разных знаков первичного алфавита могут иметь различную длину - неравномерный код.
коды могут строиться для отдельного знака первичного алфавита (алфавитное кодирование) или для их комбинаций (кодирование блоков, слов).

3.2.1. Алфавитное неравномерное двоичное кодирование сигналами равной длительности. Префиксные коды

знаки первичного алфавита (например, русского) кодируются комбинациями символов двоичного алфавита (т.е. 0 и 1).
длина кодов и, соответственно, длительность передачи отдельного кода, могут различаться.
Длительности элементарных сигналов при этом одинаковы (to = t1 = t).

Для передачи информации, в среднем приходящейся на знак первичного алфавита, необходимо время
T=K(A,2) ∙t
Построить такую схему кодирования, в которой суммарная длительность кодов при передаче данного сообщения была бы наименьшей.

Решение: коды знаков первичного алфавита, вероятность появления которых в сообщении выше, следует строить из возможно меньшего числа элементарных сигналов, а длинные коды использовать для знаков с малыми вероятностями.
Пусть получен код
00100010000111010101110000110
Каким образом он может быть декодирован?

А) Неравномерный код с разделителем
Разделителем отдельных кодов букв будет последовательность 00.
Разделителем слов-слов – 000.

Правила построения кодов:
код признака конца знака может быть включен в код буквы (т.е. коды всех букв будут заканчиваться 00);
коды букв не должны содержать двух и более нулей подряд в середине. (иначе они будут восприниматься как конец знака);
код буквы (кроме пробела) всегда должен начинаться с 1;
разделителю слов (000) всегда предшествует признак конца знака; при этом реализуется последовательность 00000.

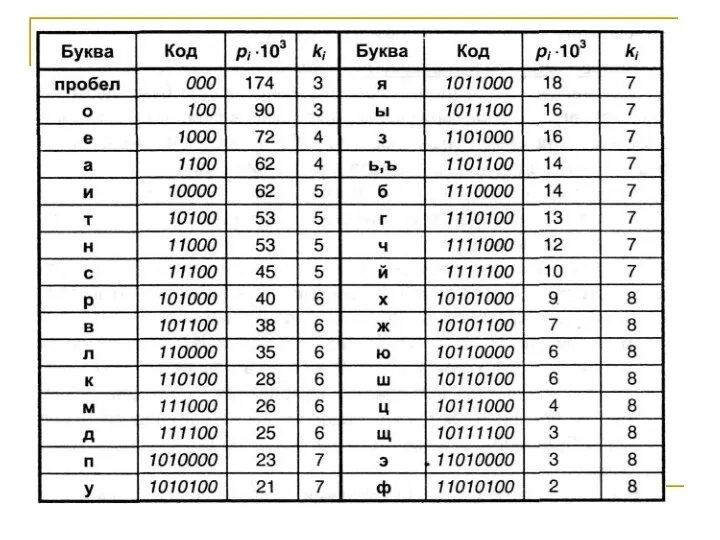
Среднюю длину кода К(r,2) для данного способа кодирования:
(по определению средней дискретной величины).

I1(r) = 4,356 бит.
Избыточность данного кода:
При данном способе кодирования будет передаваться приблизительно на 14% больше информации, чем содержит исходное сообщение.

Рассмотрев один из вариантов двоичного неравномерного кодирования, возникают вопросы:
1) Возможно ли такое кодирование без использования разделителя знаков?
2) Существует ли наиболее эффективный (оптимальный) способ неравномерного двоичного кодирования?

Неравномерный код может быть однозначно декодирован, если никакой из кодов не совпадает с началом (префиксом) какого-либо иного более длинного кода – условие ФАНО.
Например, если имеется код 110, то уже не могут использоваться коды 1, 11, 1101, 110101.

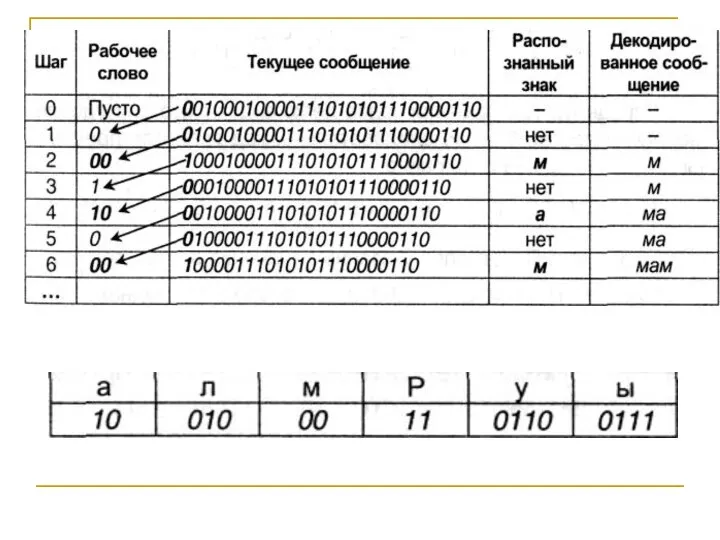
Пример 3.1.
Пусть имеется следующая таблица префиксных кодов:
Требуется декодировать сообщение:
00100010000111010101110000110

Декодирование производится циклически
1. отрезать от текущего сообщения крайний левый символ, присоединить справа к рабочему кодовому слову;
2. сравнить рабочее кодовое слово с кодовой таблицей; если совпадения нет, перейти к 1.
3. декодировать рабочее кодовое слово, очистить его;
4. проверить, имеются ли еще знаки в сообщении; если «да», перейти к 1.

Таким образом, использование префиксного кодирования позволяет делать сообщение более коротким.
Условие Фано не устанавливает способа формирования префиксного кода и, в частности, наилучшего из возможных.

В) Префиксный код Шеннона-Фано.
Данный вариант кодирования был предложен в 1948-1949 гг. независимо Р. Фано и К. Шенноном.

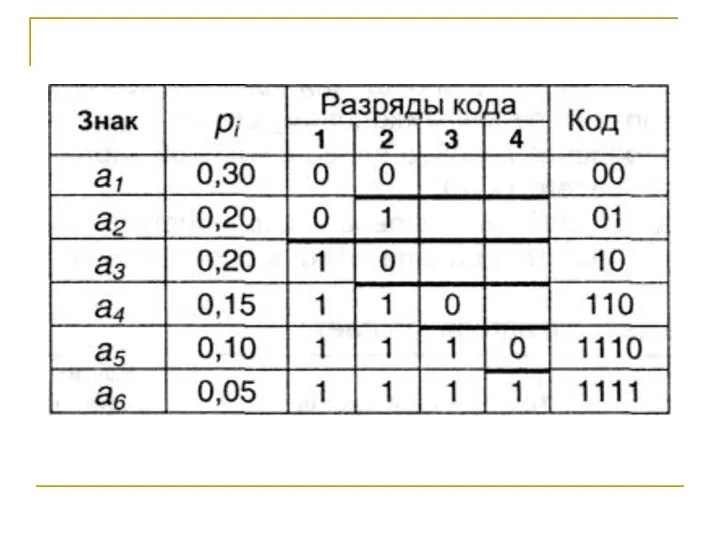
Пусть имеется первичный алфавит А, состоящий из шести знаков а1 ...а6 с вероятностями появления в сообщении, соответственно: 0,3; 0,2; 0,2; 0,15; 0,1; 0,05.
Расположим эти знаки в таблице в порядке убывания вероятностей.
Разделим знаки на две группы таким образом, чтобы суммы вероятностей в каждой из них были бы приблизительно равными. Затем будем делить следующие группы.

Средняя длина кода равна:
I1(A) = 2,390 бит.
избыточность кода Q(A,2) = 0,0249, т.е. около 2,5%.

Данный код нельзя считать оптимальным, поскольку вероятности появления 0 и 1 неодинаковы (6/17=0,35 и 11/17=0,65, соответственно).
Для русского алфавита избыточность кода Q=0,0147.

С) Префиксный код Хаффмана

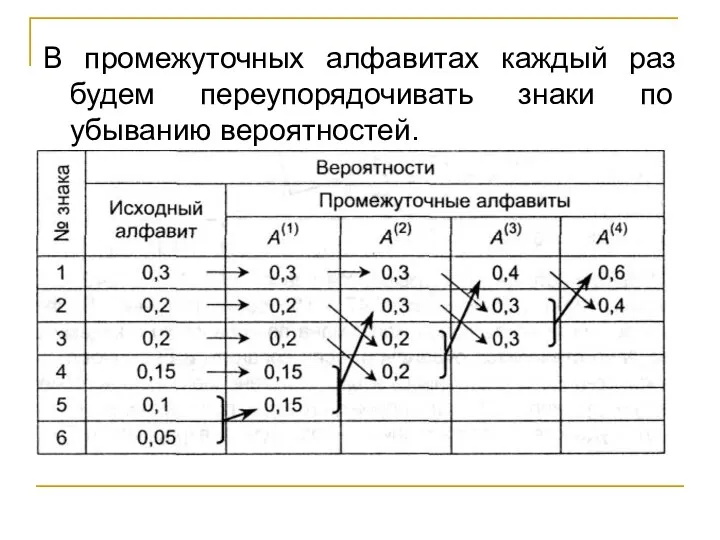
Способ оптимального префиксного двоичного кодирования был предложен Д. Хаффманом. Построение кодов Хаффмана рассмотрим на том же примере.
Создадим новый вспомогательный алфавит A1, объединив два знака с наименьшими вероятностями (а5 и а6) и заменив их одним знаком (например, а(1)); его вероятность будет равна сумме вероятностей т.е. 0,15; остальные знаки исходного алфавита включим в новый без изменений; общее число знаков в новом алфавите, очевидно, будет на 1 меньше, чем в исходном.

Аналогично продолжим создавать новые алфавиты, пока в последнем не останется два знака.
Количество таких шагов будет равно N - 2, где N - число знаков исходного алфавита (N=6, необходимо построить 4 вспомогательных алфавита).

В промежуточных алфавитах каждый раз будем переупорядочивать знаки по убыванию вероятностей.

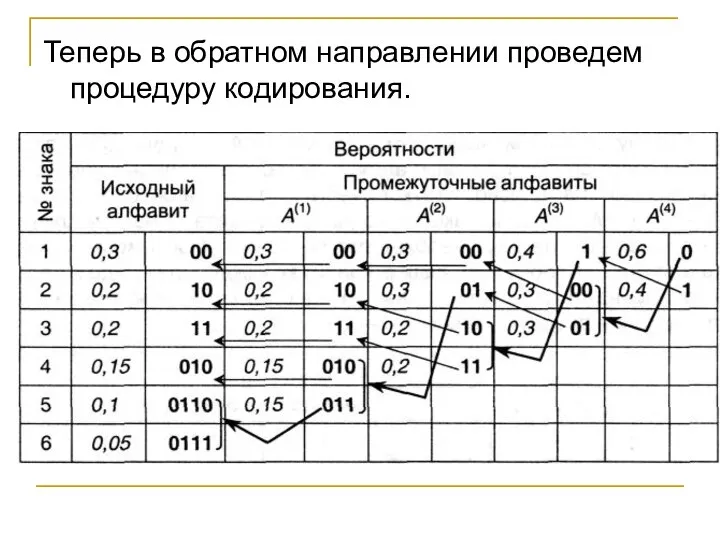
Теперь в обратном направлении проведем процедуру кодирования.

К(А,2) = 0,3 ∙ 2 + 0,2 ∙ 2 + 0,2 ∙ 2 +0,15 ∙ 3 + 0,1 ∙ 4 + 0,05 ∙ 4 = 2,45.
Q(A, 2) = 0,0249, однако, вероятности 0 и 1 сблизились (0,47 и 0,53, соответственно).
К(r,2) = 4,395; избыточность кода Q(r,2) = 0,0090, т.е. не превышает 1 %, что заметно меньше избыточности кода Шеннона-Фано.

Код Хаффмана важен в теоретическом отношении, поскольку можно доказать, что он является самым экономичным из всех возможных, т.е. ни для какого метода алфавитного кодирования длина кода не может оказаться меньше, чем код Хаффмана.

Метод Хаффмана и его модификация - метод адаптивного кодирования (динамическое кодирование Хаффмана) - нашли широчайшее применение в программах-архиваторах, программах резервного копирования файлов и дисков, в системах сжатия информации в модемах и факсах.