Содержание
- 2. Сложное высказывание Объединение нескольких простых высказываний в одно. П Р И М Е Р Е =
- 3. Приоритет логических операций: Инверсия; Конъюнкция; Дизъюнкция; Импликация и эквивалентность. П Р И М Е Р A
- 4. Построение таблицы истинности сложного высказывания Вычислить количество строк. i = 2 n + 2 строки заголовка
- 5. Задание: Постройте таблицы истинности сложных высказываний и определите, являются ли эти высказывания тождественно истинными: A &
- 6. Задание Постройте таблицу истинности сложного высказываний и определите, является ли это высказывание тождественно истинным: A →
- 7. Задание : Постройте таблицу истинности сложного высказываний и определите, является ли это высказывание тождественно истинным: 6
- 8. Задание: Постройте таблицы истинности сложных высказываний и определите, являются ли эти пары высказываний эквивалентными: A v
- 9. Задача 1 Сколько различных решений имеет уравнение (K ^ L ^ M) v (¬L ^ ¬M
- 10. Задание 3: Укажите значения логических переменных K, L, M, N, при которых логическое выражение (K \/
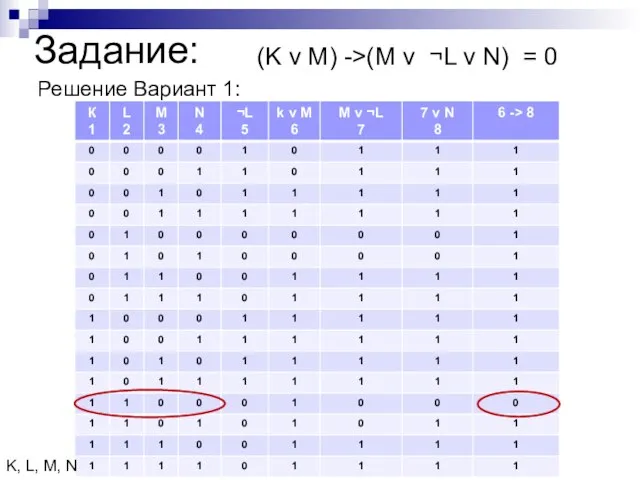
- 11. Задание: (K v M) ->(M v ¬L v N) = 0 Решение Вариант 1: K, L,
- 12. Задание: (K v M) -> (M v ¬L v N) = 0 var k, l, m,
- 13. Задание: (K v M) -> (M v ¬L v N) = 0 var k, l, m,
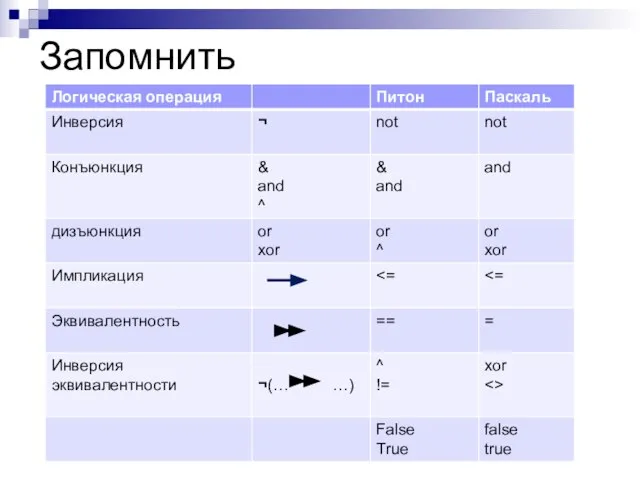
- 14. Запомнить
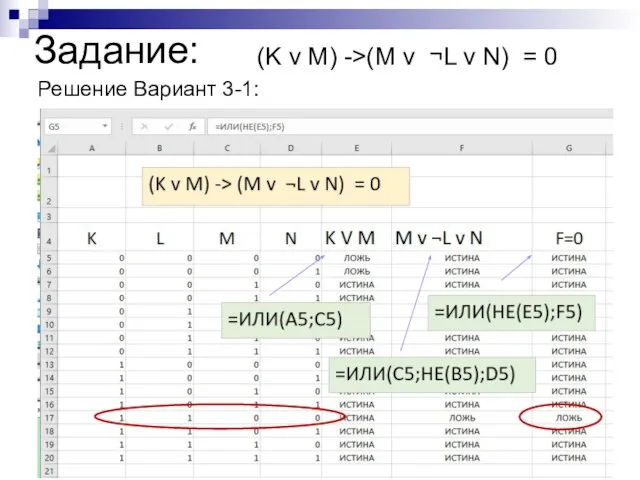
- 15. Задание: (K v M) ->(M v ¬L v N) = 0 Решение Вариант 3-1:
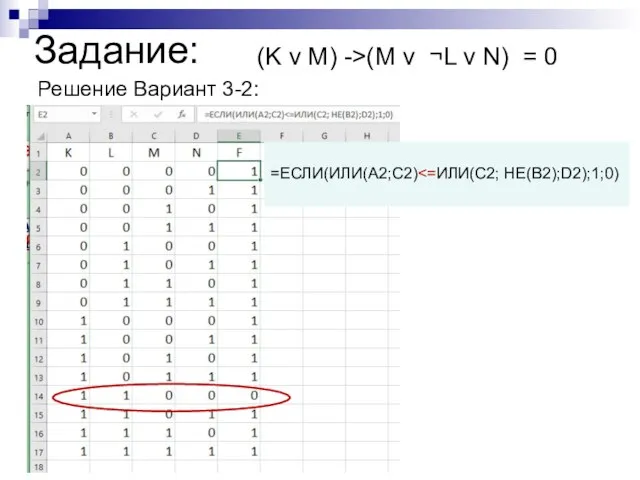
- 16. Задание: (K v M) ->(M v ¬L v N) = 0 Решение Вариант 3-2: =ЕСЛИ(ИЛИ(A2;C2)
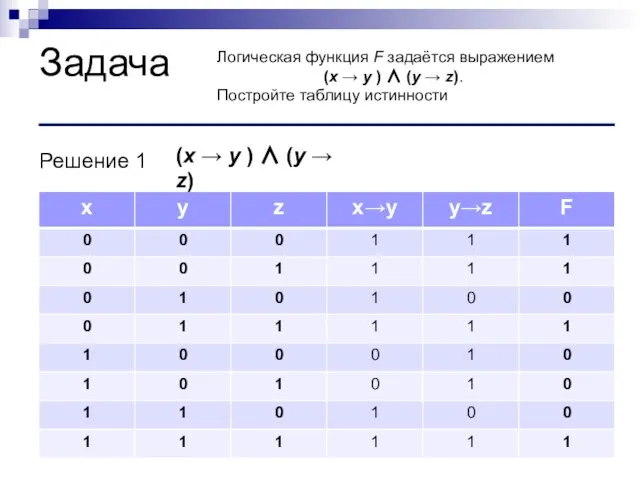
- 17. Задача Логическая функция F задаётся выражением (x → y ) ∧ (y → z). Постройте таблицу
- 18. Задача Логическая функция F задаётся выражением (x → y ) ∧ (y → z). Постройте таблицу
- 20. Скачать презентацию












 Лето в Кванториуме
Лето в Кванториуме Сообщество Детский нейропсихолог. Нейрокоррекция
Сообщество Детский нейропсихолог. Нейрокоррекция Разработка виртуального тренажера процесса пастеризации в среде Labview
Разработка виртуального тренажера процесса пастеризации в среде Labview Факторы, влияющие на защиту информации
Факторы, влияющие на защиту информации Базы данных. Пример
Базы данных. Пример Asymptotic Analysis
Asymptotic Analysis Службы Андроид
Службы Андроид Средства поиска информации в Интернете для культурологов
Средства поиска информации в Интернете для культурологов LR9-10_2ch__Diskretnoe_tsifrovoe_predstavlenie_textovoy_graficheskoy_zvukovoy_informatsii_i_videoinformatsii
LR9-10_2ch__Diskretnoe_tsifrovoe_predstavlenie_textovoy_graficheskoy_zvukovoy_informatsii_i_videoinformatsii Конфиденциальность в интернете
Конфиденциальность в интернете Урок информатики. 3 класс. Единичное имя объекта. выполнила: Ишбирдина Т.Н. учитель МОУ Кулуевская СОШ
Урок информатики. 3 класс. Единичное имя объекта. выполнила: Ишбирдина Т.Н. учитель МОУ Кулуевская СОШ Компьютерные сети
Компьютерные сети Алгоритмы и исполнители
Алгоритмы и исполнители Документ и его создание
Документ и его создание 9-1-2
9-1-2 Web-программирование. Лекция 5. Шаблоны проектирования
Web-программирование. Лекция 5. Шаблоны проектирования Жизненный цикл современной программной системы
Жизненный цикл современной программной системы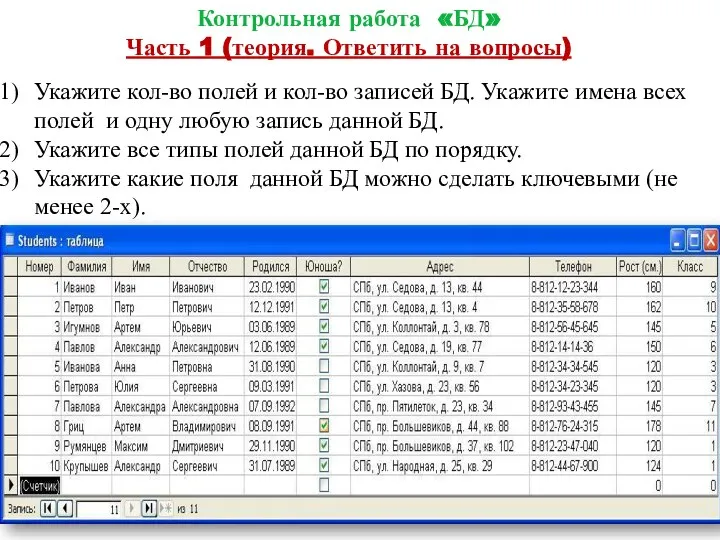 1. Контрольная работа БД. Часть 1 (теория. Ответить на вопросы)
1. Контрольная работа БД. Часть 1 (теория. Ответить на вопросы) Служба информационной безопасности предприятия: функции, структура, деятельность, документационное обеспечение
Служба информационной безопасности предприятия: функции, структура, деятельность, документационное обеспечение Шаблон презентации по информатике
Шаблон презентации по информатике Полный цикл разработки JS
Полный цикл разработки JS Внешние устройства компьютера
Внешние устройства компьютера Что такое штрих-код
Что такое штрих-код Универсальная битва полов
Универсальная битва полов Презентация на тему Типы модулей в Delphi
Презентация на тему Типы модулей в Delphi  База данных SQLite. Лекция 12
База данных SQLite. Лекция 12 Действия с файлами и каталогами
Действия с файлами и каталогами Логические операции. Логические формулы
Логические операции. Логические формулы