Представление чисел в памяти компьютера

Что такое система счисления?
Что такое основание системы счисления?
Какие системы счисления используются в ПК?
Какой алфавит и основание имеет двоичная система счисления?
Какой алфавит и основание имеет десятичная система счисления?
Как перевести число из двоичной системы счисления в десятичную?
Как перевести число из десятичной системы счисления в двоичную?
Каковы правила сложения двоичных чисел.

Образ компьютерной памяти

Главные правила представления данных в компьютере

Правило 1
Данные (и программы) в памяти компьютера хранятся в двоичном виде, т. е. в виде цепочек единиц и нулей.

Правило 2
Представление данных в компьютере дискретно.
Дискретное множество состоит из отделенных друг от друга элементов.

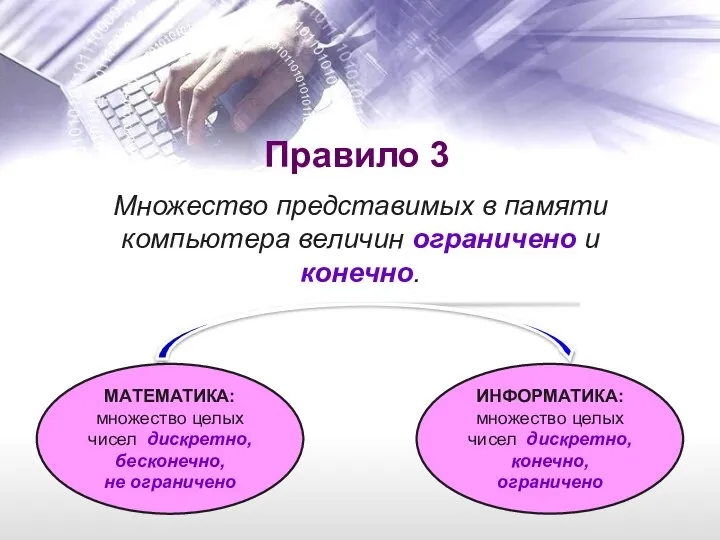
Правило 3
Множество представимых в памяти компьютера величин ограничено и конечно.
МАТЕМАТИКА:
множество целых чисел дискретно, бесконечно,
не ограничено
ИНФОРМАТИКА:
множество целых чисел дискретно, конечно, ограничено

Правило 4
В памяти компьютера числа хранятся в двоичной системе счисления.

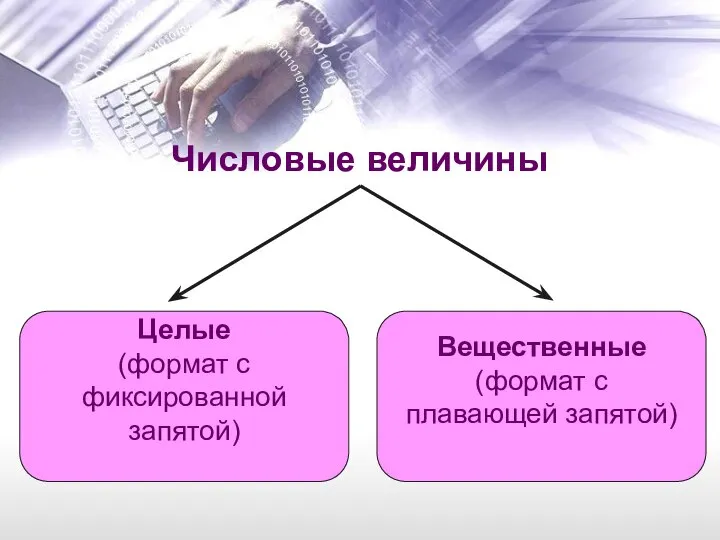
Числовые величины
Целые
(формат с
фиксированной запятой)
Вещественные
(формат с
плавающей запятой)

Для хранения целых неотрицательных чисел без знака отводится одна ячейка памяти (8 битов).
7 6 5 4 3 2 1 0
Номера разрядов
Биты, составляющие
число
Минимальное число 0
Максимальное число 25510
111111112 = 1000000002 -1 = 28 – 1 = 25510
Для n-разрядного представления максимальное целое неотрицательное число равно 2n – 1.
Целые числа без знака

Пример. Представить число 5110 в двоичном виде в восьмибитовом представлении в формате целого без знака.
Решение.
5110 = 1100112
Целые числа без знака

Для хранения целых чисел со знаком отводится
две ячейки памяти (16 битов).
Старший разряд числа определяет его знак.
Если он равен 0, число положительное,
если 1, то отрицательное.
5110 = 1100112
- 5110 = - 1100112
Такое представление чисел в компьютере называется
прямым кодом.
Целые числа со знаком

Для n-разрядного представления со знаком (с учетом выделения одного разряда на знак):
минимальное отрицательное число равно – 2n-1
максимальное положительное число равно 2n-1 – 1,
Целые числа в памяти компьютера —
это дискретное, ограниченное и конечное множество.
Целые числа со знаком

Для представления отрицательных целых чисел используется дополнительный код.
Алгоритм получения дополнительного кода отрицательного числа:
Число записать прямым кодом в n двоичных разрядах.
Получить обратный код числа, для этого значения всех битов инвертировать, кроме старшего разряда.
К полученному обратному коду прибавить единицу.
Представить число -201410 в двоичном виде в шестнадцатибитном представлении в формате целого со знаком.
Целые числа со знаком

Алгебраическое сложение двоичных чисел
Положительные слагаемые представить в прямом коде.
Отрицательные слагаемые – в дополнительном.
Найти сумму кодов, включая знаковые разряды, которые при этом рассматриваются как старшие разряды. При переносе из знакового разряда единицу переноса отбрасывают.
В результате получают алгебраическую сумму в прямом коде, если эта сумма положительная, и в дополнительном, если сумма отрицательная.
Целые числа со знаком

Пример 1. Найти разность 1310 – 1210 в восьмибитном представлении.
Так как произошел перенос из знакового разряда,
первую единицу отбрасываем, и в результате
получаем 00000001.
Целые числа со знаком

Пример 2. Найти разность 810 – 1310 в восьмибитном представлении.
Целые числа со знаком

Пример 2. Найти разность 810 – 1310 в восьмибитном представлении.
В знаковом разряде стоит 1, значит результат получен в дополнительном коде. Прейдем от дополнительного кода к обратному, вычтя единицу:
Прейдем от обратного кода к прямому, инвертируя все цифры, за исключением знакового (старшего) разряда: 100001012 = 510.
Целые числа со знаком

Вещественные числа хранятся и обрабатываются в компьютере в формате с плавающей запятой, использующем экспоненциальную форму записи чисел.
A = M ? qn
M – мантисса числа (правильная отличная от нуля дробь),
q – основание системы счисления,
n – порядок числа.
Диапазон ограничен максимальными значениями M и n.
Вещественные числа

Вещественные числа
Например, 123,45 = 0,12345 · 103
Порядок указывает, на какое количество позиций и в каком направлении должна сместиться десятичная запятая в мантиссе.
Число в формате с плавающей запятой может занимать в памяти 4 байта (обычная точность) или 8 байтов (двойная точность).
При записи числа выделяются разряды для хранения знака мантиссы, знака порядка, порядка и мантиссы.
Мантисса M и порядок n определяют диапазон изменения чисел и их точность.