Слайд 2Мы знали, но забыли
Устойчивость – это когда всё стабильно?

Слайд 3В любой сложной системе есть запаздывание:
Подали напряжение на двигатель
Подождали полсекундочки
Обороты вышли на

стабильную величину
Слайд 4В любой сложной системе есть запаздывание:
Опустили монетку в снековый автомат
Подождали 2 минуты
Получили

круассан
Слайд 5В любой сложной системе есть запаздывание:
Посмотрели на светофор
Загорелся зеленый
Подождали секунду-две (в среднем)
Перешли

дорогу
Слайд 6Запаздывание?
Как оценить величину запаздывания?
Подать на систему сигнал
Измерить запаздывание

Слайд 7Запаздывание?
Как оценить величину запаздывания?
Подать на систему сигнал
Измерить запаздывание
А как?
Время достижения установившегося

значения?
А какую точность брать?
Слайд 8Как будет удобнее?
Сигналы бывают разные
Постоянный сигнал
Скачок
Пила
Треугольник
Шум
Синус

Слайд 9Как будет удобнее?
Любой периодический сигнал можно представить суммой гармонических сигналов разных частот

и амплитуд.
Если сигнал непериодический, то можно раскладывать в ряд Фурье на интервале.
Попробуем оперировать частотным представлением сигналов для оценки запаздывания
Слайд 10Эксперимент
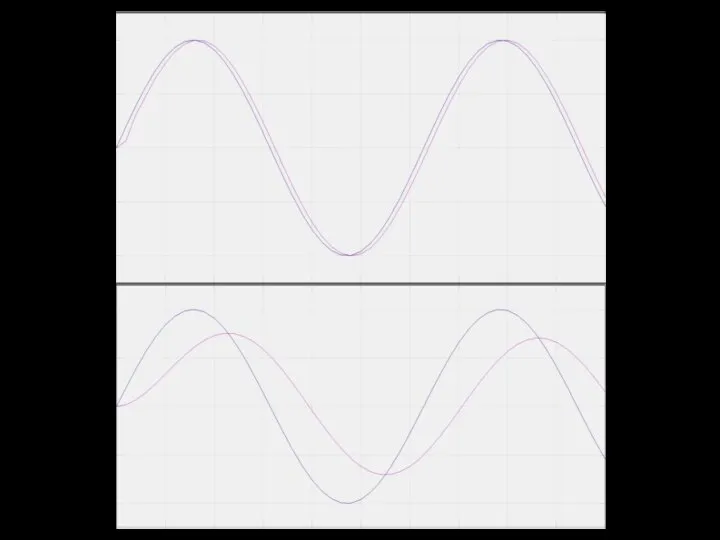
Будем подавать на объект чистые синусоиды и наблюдать за реакцией объекта
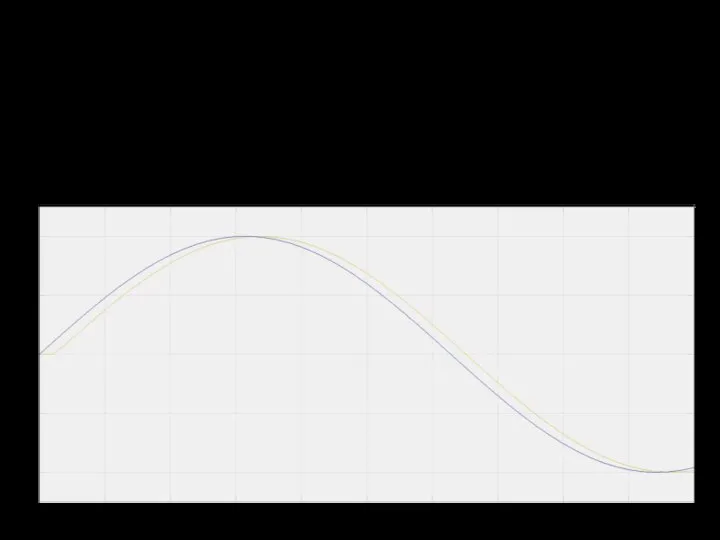
Слайд 11Эксперимент
Будем подавать на объект чистые синусоиды и наблюдать за реакцией объекта
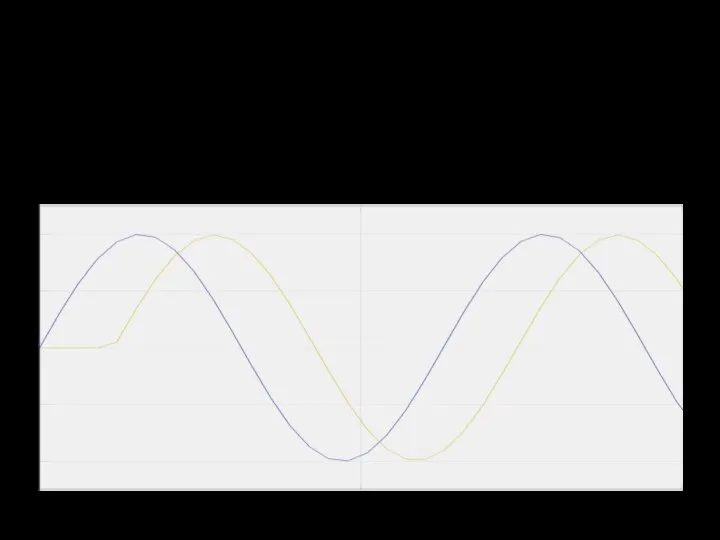
Слайд 12Эксперимент
Будем подавать на объект чистые синусоиды и наблюдать за реакцией объекта
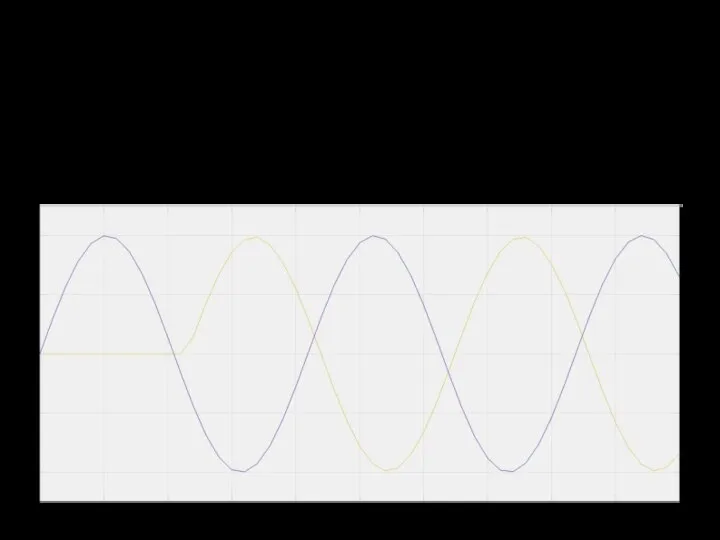
Слайд 13Что это нам дает?
В эксперименте время запаздывания было постоянным на всех частотах,

в реальной жизни такое бывает не всегда.
На каждой отдельно взятой синусоиде запаздывание удобно оценивать углом
Xвх = A * sin(wt)
Xвых = B * sin(wt + phi)
phi – это угол запаздывания
Слайд 14При чем тут устойчивость?
Пора вспомнить, чем мы тут занимаемся
Основной принцип управления объектами

– управление по ошибке.
Когда из заданного сигнала вычитается выходной и результат подаётся на регулятор.
Xвх - Xвых = A * sin(wt) – B * sin(wt + phi)
Если phi = Pi, то
Xвых = B * sin(wt + Pi) = -B * sin(wt)
Слайд 15При чем тут устойчивость?
То есть отрицательная обратная связь становится положительной!
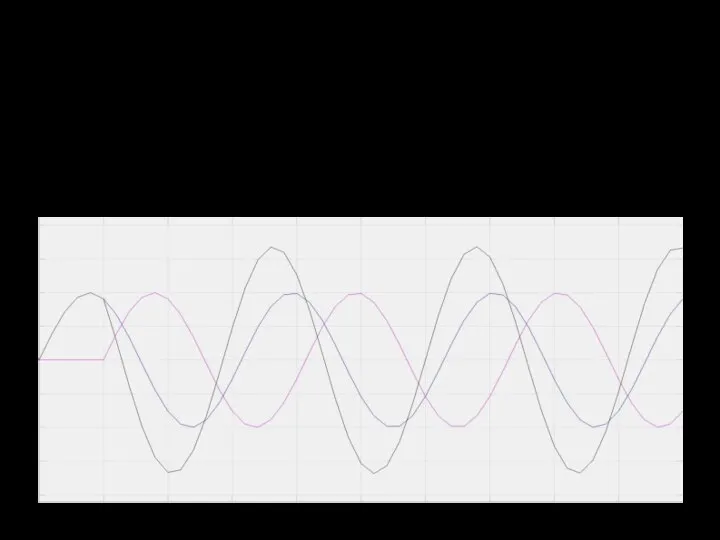
Слайд 16Насколько это плохо?
Xвх - Xвых = A * sin(wt) + B *

sin(wt)
= (A + B) * sin(wt)
На следующем шаге на объект будет подаваться уже Xвх = (A + B) * sin(wt)
Таким образом, выход будет (A + B) * B / A
Ошибка на следующем шаге будет равна:
Xвх - Xвых = (A + (A + B) * B / A) * sin(wt)
Слайд 17Упростим
Для удобства примем А = 1:
Xвх - Xвых = (1 + B)

* sin(wt)
Xвх - Xвых = (1 + B*(1 + B)) * sin(wt)
Xвх - Xвых = (1 + B*(1 + B*(1 + B))) * sin(wt)
Xвх - Xвых = (1 + B*(1 + B*(1 + B*(1 + B)))) * sin(wt)
Xвх - Xвых = (1 + B*(1 + B*(1 + B*(1 + B*(1 + B))))) * sin(wt)
Будет ли этому конец?
Слайд 18Проще не стало
Оставим только амплитуду синуса, сам синус больше 1 не станет

точно:
|Xвх – Xвых| = (1 + B)
|Xвх – Xвых| = (1 + B*(1 + B)) = 1 + B + B^2
|Xвх – Xвых| = (1 + B*(1 + B + B^2)) = 1 + B + B^2 + B^3
Каждый следующий шаг – сумма ряда B^n
Если B < 1, то сумма ряда не бесконечность, значит, модуль ошибки (и выходного значения заодно) будут ограничены.
Сумма ряда 1 + B + B^2 + B^3 + ... = 1/(1 - B)
Слайд 19Для наглядности
Если B = 0.9, то амплитуда синусоиды ошибки будет стремиться к

10 при входном сигнале в 1, а амплитуда выхода – к 10–1=9.
При B = 0.01 – выход будет синусоидой с амплитудой 0.(01), что выглядит уже не так пугающе.
Слайд 20Что такое B?
B – отношение амплитуды выходного сигнала ко входному на частоте,

запаздывание на которой равно Pi радиан (180 градусов).
Слайд 21Что мы узнали?
1) Как обычно описывают запаздывание
2) Как оно может навредить системе
3)

В каких случаях запаздывание приведёт к развалу системы
4) Есть какие-то частотные штуки, которые мешают жить
Слайд 22Запаздывание? Никогда не встречал
Бывает ли чистое запаздывание в жизни?
На самом деле чистое

запаздывание в нашем мире встречается не очень часто. Обычно запаздывание является следствием протекания внутренних процессов, а не отсутсвием реакции на вход вовсе.
Это значит, что есть ряд внутренних переменных объекта, которые меняются плавно, создавая задержку между выходом и входом.
Слайд 23Запаздывание? Никогда не встречал
Двигатель не набирает скорость мгновенно? - это ток не

может резко нарасти и инерция ротора ограничивает ускорение
Человек не сразу переходит дорогу с появлением зелёного – это информация от глаз обрабатывается мозгом.
Наиболее подходящим примером транспортной задержки можно считать задержки в линиях связи.
Слайд 24Что это нам даёт?
Это означает, что при увеличении частоты синуса на входе

значения внутренних переменных объекта будут не успевать отрабатывать полную амплитуду входного сигнала
Слайд 26Объекты в жизни
Посмотрим на возможное поведение коэффициента передачи объектов при увеличении частоты

входного сигнала:
1) Не меняется вообще
2) Убывает в большом
3) Возрастает в большом
Слайд 27Объекты в жизни
Как мы только что убедились, запаздывание, в основном, приносит вместе

с собой уменьшение амплитуды при повышении частоты. Если амплитуда не меняется совсем, то, скорее всего, вход и выход связаны между собой линейно.
Такие объекты сложно вывести из равновесия и для управления обратная связь не нужна вовсе.
Слайд 28Объекты в жизни
Второй вариант – наиболее распространённый случай. Стабильные объекты обычно обладают

фильтрующими свойствами (снижают амплитуду при увеличении частоты).
Если коэффициент передачи будет меньше единицы на частотах с углом запаздывания не меньше 180 градусов, то объект будет устойчивым.
Большинство объектов и явлений устойчивы
Слайд 29Объекты в жизни
Третий вариант – тоже довольно редкий. В качестве примера можно

привести тахогенератор, на вход которому приходит изменение угла, а на выходе снимается изменение напряжения. Чем выше частота изменения угла, тем выше скорость, а, следовательно, и ЭДС на обмотке.
Говорить об устойчивости подобного объекта можно с натяжкой.
Слайд 30Куда уходит устойчивость?
Если объекты вокруг устойчивы, то к чему тогда весь разговор?

Слайд 31Куда уходит устойчивость?
Объекты устойчивы, когда мы не пытаемся ими управлять!
А вот наша

система управления может значительно снизить устойчивость или вообще стать неустойчивой.
Поэтому вопрос устойчивости поднимается именно в рамках системы управления.
Слайд 32Что мы узнали ещё?
1) Большинство объектов устойчиво
2) Устойчивость уменьшает система управления
3) Человек

всё портит
Слайд 33Как сильно всё испорчено?
Как оценить, сильно снизилась устойчивость или нет?

Слайд 34Как сильно всё испорчено?
Можно определить, насколько далеко от текущей ситуации находится неустойчивое

положение.
Обычно, это называется запасом.
Слайд 35Запасы устойчивости
Выйти из зоны устойчивости объект может двумя путями:
1) Если коэффициент передачи

увеличится настолько, что на углу запаздывания 180 градусов он станет равным единице.
2) Если угол запаздывания увеличится настолько, что на коэффициенте передачи 1 он достигнет значения 180 градусов.
Слайд 36Бывает ли такое?
Для примера возьмём двигатель
1) Нагрелись обмотки из-за работы на большую

нагрузку и сопротивление увеличилось. Это изменение приведет к увеличению коэффициента передачи системы.
2) Обмотки сильно нагрелись, диаметр витков от нагрева увеличился, увеличилась магнитная проницаемость материала сердечника. Результат – изменилась индуктивность, постоянная времени L/R, увеличился угол запаздывания
Слайд 37Как проверить систему на устойчивость
Снять зависимости амплитуды и угла запаздывания от частоты
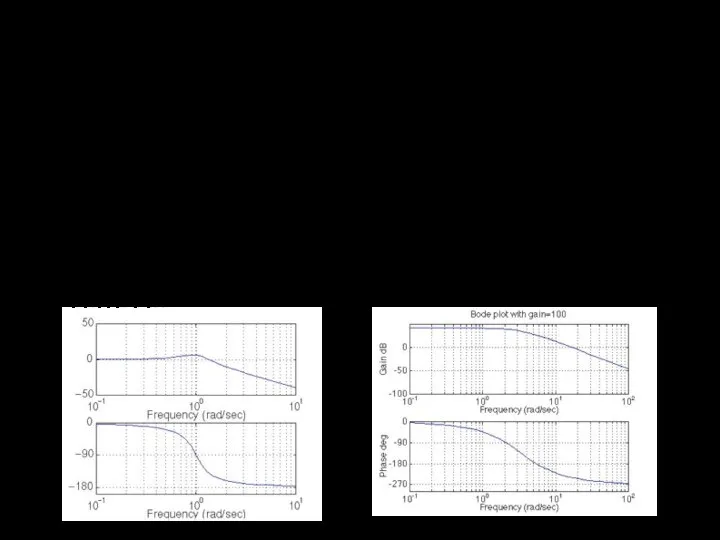
на диапазоне от 0 до той, на которой угол будет 180 градусов
Определить по снятой характеристике оба запаса.
Слайд 38Как проверить систему на устойчивость
А если у нас микроконтроллер и преобразование Фурье

нам делать слишком дорого?
Слайд 39Как проверить систему на устойчивость
Можно искуственно создать изменения в системе и оценить

величину запасов:
1) Увеличить коэффициент усиления в прямом канале до тех пор, пока в системе не начнуться устойчивые колебания.
2) Внести искуственную задержку в прямой канал, увеличивать её до появления устойчивых колебаний.
Слайд 40Проблемы автоматизации
Чтобы автоматизировать процесс, надо уметь определять устойчивые колебания.
Они могут прийтись на

ту частоту, которая будет выше частоты чтения выходной величины.






































 FitnesPro Приложение-помощник для занятий фитнесом
FitnesPro Приложение-помощник для занятий фитнесом Программа ClickMeeting
Программа ClickMeeting Интернет. История развития интернета
Интернет. История развития интернета Классификация компьютерных объектов
Классификация компьютерных объектов Пошаговая инструкция создания сводной таблицы в excel
Пошаговая инструкция создания сводной таблицы в excel Растровые графические редакторы
Растровые графические редакторы Адекватность моделей моделируемым объектам и целям моделирования
Адекватность моделей моделируемым объектам и целям моделирования Массивы. Операции с массивами
Массивы. Операции с массивами Системы управления базами данных (I часть)
Системы управления базами данных (I часть) Видеомэйкинг. От нуба – тянущимся к знаниям
Видеомэйкинг. От нуба – тянущимся к знаниям Орнитология в интернете: сайты, сообщества, базы данных,
Орнитология в интернете: сайты, сообщества, базы данных, Презентация на тему Звуковые карты
Презентация на тему Звуковые карты  Финграмотность – это тема
Финграмотность – это тема Game Studies, уличная фотография в видеоиграх
Game Studies, уличная фотография в видеоиграх Ошибки операторов при работе с БД ОВЗ
Ошибки операторов при работе с БД ОВЗ Requesting Access - BW Reports (Operations Dashboard)
Requesting Access - BW Reports (Operations Dashboard) Adeon Hosting. Интернет-магазин игр. Создай свой сервер с нуля
Adeon Hosting. Интернет-магазин игр. Создай свой сервер с нуля Программное обеспечение: Уровни и классификация
Программное обеспечение: Уровни и классификация Схемотехника аналоговых устройств
Схемотехника аналоговых устройств Исполнители вокруг нас
Исполнители вокруг нас Рабочий стол и подсистемы
Рабочий стол и подсистемы Как выбрать робота для торговли на Foreх
Как выбрать робота для торговли на Foreх Элементы алгебры логики. Математические основы информатики. 8 класс
Элементы алгебры логики. Математические основы информатики. 8 класс Основные правила записи формул Виды формул
Основные правила записи формул Виды формул Современные веб-технологии. Лекция 2.1
Современные веб-технологии. Лекция 2.1 REST in peace?
REST in peace? Антивирусные программы
Антивирусные программы Введение в информатику. Лекция 1
Введение в информатику. Лекция 1