Содержание
- 2. Рекурсия – способ определения множества объектов через само это множество на основе заданных простых базовых случаев.
- 3. У попа была собака, он её любил, Она съела кусок мяса, он её убил, В землю
- 4. Рекурсивная процедура (функция) – это процедура(функция), которая вызывает сама себя напрямую или через другие процедуры и
- 5. Задача: Вычислите сумму всех цифр числа def df(n): s = n % 10 if n >=
- 9. Скачать презентацию






 Арифметические приложения теории сравнений
Арифметические приложения теории сравнений Проект RJ company
Проект RJ company Создание рабочего стола
Создание рабочего стола Расширение Live Server
Расширение Live Server Базы данных в MS Excel-1
Базы данных в MS Excel-1 ИТ-марафон
ИТ-марафон Системная и программная инженерия. Спринт 10.04 – 24.04. Презентация программного продукта
Системная и программная инженерия. Спринт 10.04 – 24.04. Презентация программного продукта Создаем игру Fifa
Создаем игру Fifa Базовая навигация в SAP
Базовая навигация в SAP MeSH Медицинский предметный указатель
MeSH Медицинский предметный указатель Адаптивная верстка
Адаптивная верстка Game over
Game over Интерфейс Rhinoceros и Grasshopper
Интерфейс Rhinoceros и Grasshopper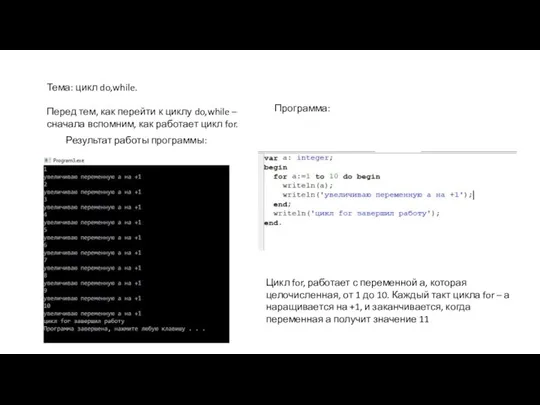 Цикл do, while
Цикл do, while Ввод-вывод данных на консоль в С++
Ввод-вывод данных на консоль в С++ Измерение информации. 7 класс
Измерение информации. 7 класс Первоначальная работа с VHMS
Первоначальная работа с VHMS Оплата услуг онлайн на официальном сайте НГУЭУ посредством эквайринга
Оплата услуг онлайн на официальном сайте НГУЭУ посредством эквайринга Презентация на тему Применение систем счисления
Презентация на тему Применение систем счисления  Рекурсивные алгоритмы. Подготовка к ЕГЭ, задание 11
Рекурсивные алгоритмы. Подготовка к ЕГЭ, задание 11 Процессы поиска информации
Процессы поиска информации Указатели. Общие сведениях об указателях
Указатели. Общие сведениях об указателях Python. Циклы. Урок 4
Python. Циклы. Урок 4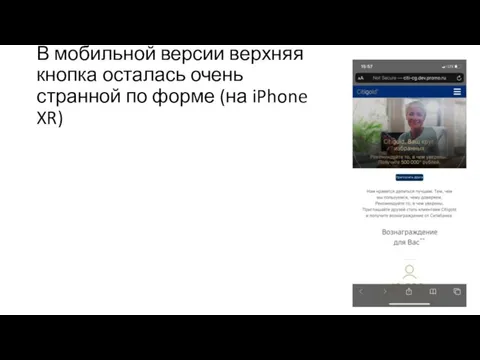 Поправить Internet Explorer
Поправить Internet Explorer Транспортування сигнальної інформації в мережах IP
Транспортування сигнальної інформації в мережах IP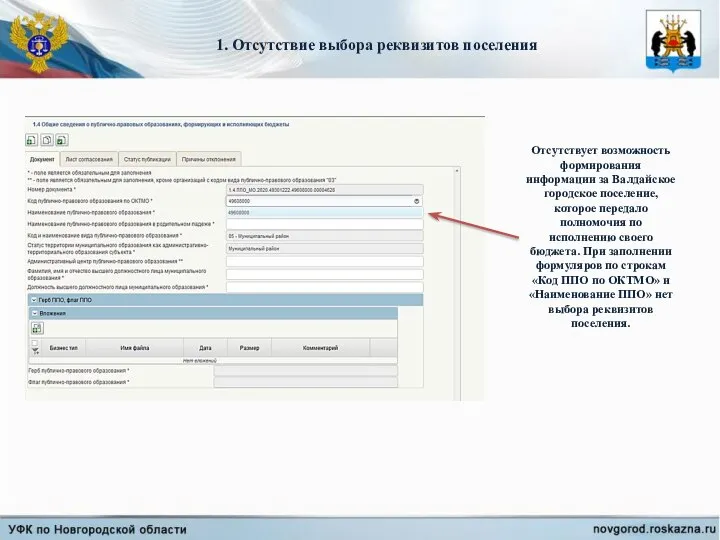 Отсутствие выбора реквизитов поселения
Отсутствие выбора реквизитов поселения Что такое онлайн-приглашение
Что такое онлайн-приглашение Лекция 2. История развития вычислительной техники
Лекция 2. История развития вычислительной техники