Слайд 4Если группировка проводится по количественном признаку, оптимальное количество групп определяется по формуле

американского ученого Стерджесса:
n=1+3,322 lgN, где
N – число единиц совокупности;
n – число групп.
Слайд 7Пример для равных интервалов. Требуется провести группировку с равными интервалами по данным

об уровне месячной заработной платы работников, которая колеблется в пределах от 600 до 750 руб. Требуется выделить 5 групп.
600-630
630-660
660-690
690-720
720-750
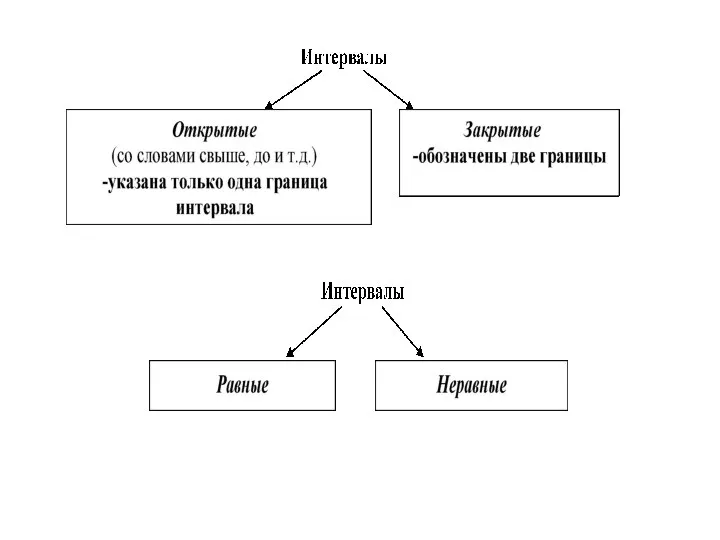
Слайд 8Неравные интервалы могут быть:
1) прогрессивно возрастающие;
2) прогрессивно убывающие;
3) произвольные.

Прогрессивно возрастать или прогрессивно убывать значения интервалов могут:
- в арифметической прогрессии:
hi+1=hi+a
- в геометрической прогрессии:
hi+1=hi*q
Если прогрессия возрастающая, а>0, q>1.
Если прогрессия убывающая, а<0, q<1.
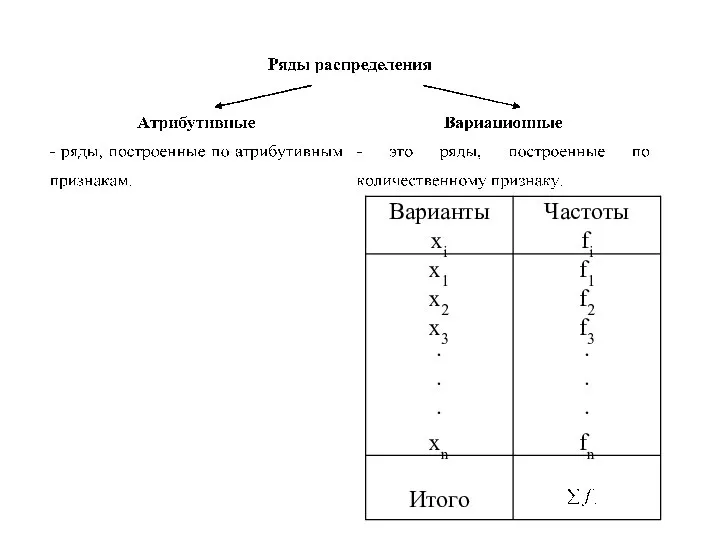
Слайд 10Частоты могут быть выражены в виде:
- числа, абсолютного значения;
- доли (сумма=1);
-

процентов (сумма=100%).
Если частоты выражены относительными величинами (доли, проценты), то они носят название – частости.
Слайд 14
Структурная группировка по 1 признаку.
n=1 +3,322lgN=
i=
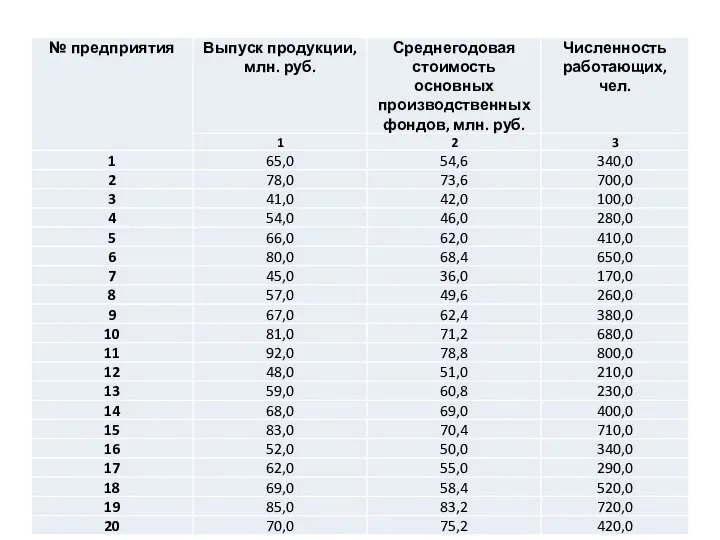
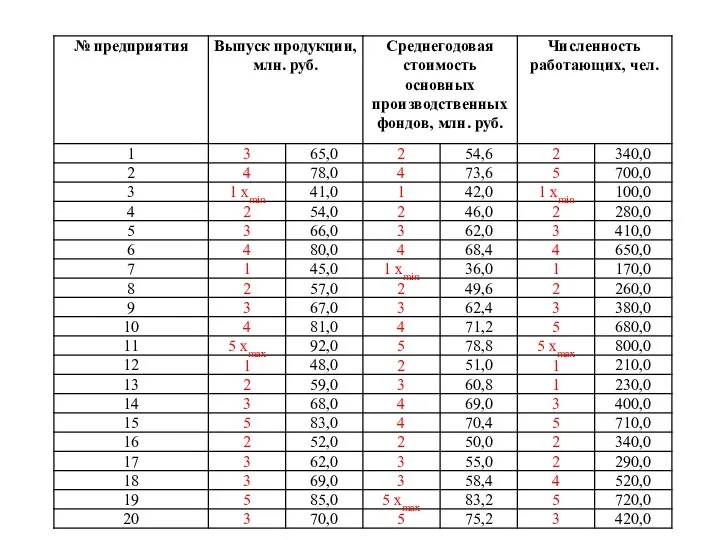
Таблица 1
Структурная группировка по выпуску продукции

Слайд 16Структурная группировка по 1 признаку.
n=1 +3,322lg20=5
Таблица 1
Структурная группировка по выпуску продукции

Слайд 17Структурная группировка по 2 признаку.
Таблица 2
Структурная группировка по среднегодовой стоимости
основных производственных

фондов
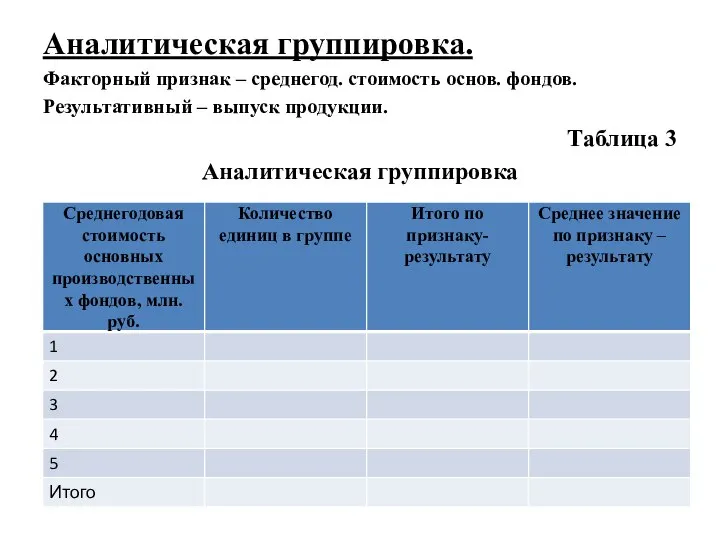
Слайд 18Аналитическая группировка.
Факторный признак – среднегод. стоимость основ. фондов.
Результативный – выпуск продукции.
Таблица 3
Аналитическая группировка
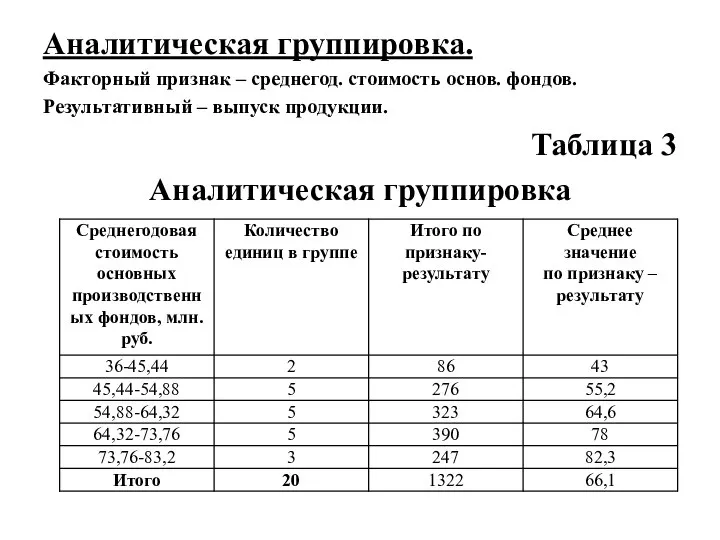
Слайд 19Аналитическая группировка.
Факторный признак – среднегод. стоимость основ. фондов.
Результативный – выпуск продукции.
Таблица 3
Аналитическая группировка










 Средневековая криптография
Средневековая криптография Анимированные ребусы
Анимированные ребусы Современные веб-технологии. Лекция 2.1
Современные веб-технологии. Лекция 2.1 Криптосистема RSA
Криптосистема RSA Разработка фирменного стиля для научной библиотеки
Разработка фирменного стиля для научной библиотеки Настройка веб-сервера (07)
Настройка веб-сервера (07) Финальные задачи. Уроки по Spike Prime
Финальные задачи. Уроки по Spike Prime Введение в курс. Криптографическая защита информации
Введение в курс. Криптографическая защита информации Основы телекоммуникаций сетей. Технологии телекоммуникационных сети TCP/IP
Основы телекоммуникаций сетей. Технологии телекоммуникационных сети TCP/IP JavaScript. Обзор
JavaScript. Обзор Создание сайта
Создание сайта Перечисления
Перечисления Атрибуты точки POI
Атрибуты точки POI Создание публикации в программе Microsoft Publisher В рамках создания тематического учебного проекта
Создание публикации в программе Microsoft Publisher В рамках создания тематического учебного проекта Космические системы ретрансляции. Радио-ретрансляция и оптическая ретрансляция
Космические системы ретрансляции. Радио-ретрансляция и оптическая ретрансляция Пройди сам и расскажи другим: как сделать эколого-краеведческий путеводитель
Пройди сам и расскажи другим: как сделать эколого-краеведческий путеводитель Приложения для анализа состояния кожи
Приложения для анализа состояния кожи Арифметические операции. Модуль 1. Занятие 4
Арифметические операции. Модуль 1. Занятие 4 Ввод сз в действие
Ввод сз в действие Keep It Green — списки дел без занудства
Keep It Green — списки дел без занудства Программное обеспечение ПК
Программное обеспечение ПК Zakony_logiki_Ravnosilnye_preobrazovania
Zakony_logiki_Ravnosilnye_preobrazovania ЕГЭ. Информатика, задание 1
ЕГЭ. Информатика, задание 1 Теория игр. Аналитическая работа по статье Croson “Gender and Culture”
Теория игр. Аналитическая работа по статье Croson “Gender and Culture” Поведение в интернете
Поведение в интернете Компьютер И все составляющие части
Компьютер И все составляющие части Знакомство с программой PowerPoint
Знакомство с программой PowerPoint Встроенные функции и их использование
Встроенные функции и их использование