Статистика. Обработка и представление результатов исследования с помощью MS Excel

Меры центральной тенденции.

Меры изменчивости

Меры изменчивости

Нормальное распределение
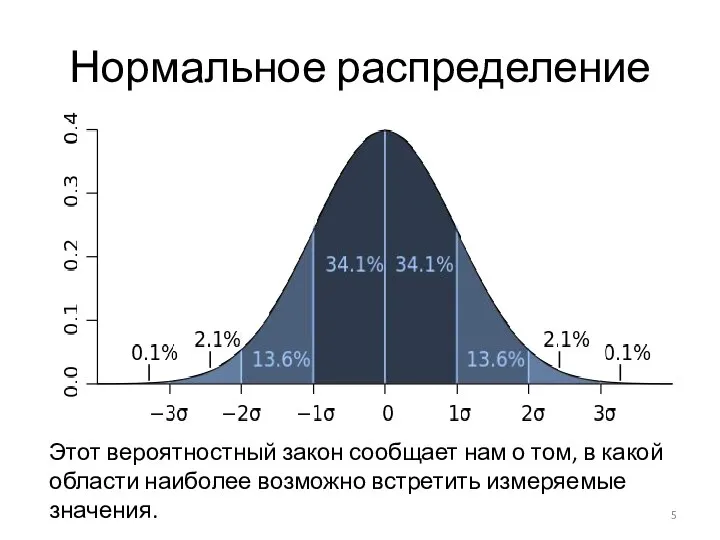
Этот вероятностный закон сообщает нам о том, в какой области наиболее возможно встретить измеряемые значения.

Нормальное распределение
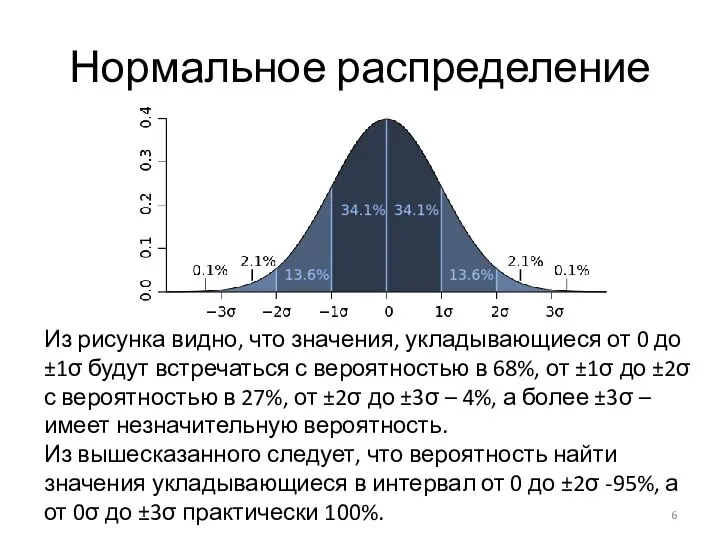
Из рисунка видно, что значения, укладывающиеся от 0 до ±1σ будут встречаться с вероятностью в 68%, от ±1σ до ±2σ с вероятностью в 27%, от ±2σ до ±3σ – 4%, а более ±3σ – имеет незначительную вероятность.
Из вышесказанного следует, что вероятность найти значения укладывающиеся в интервал от 0 до ±2σ -95%, а от 0σ до ±3σ практически 100%.

Коэффициент корреляции Пирсона
Соотношение х и у линейное, если прямая линия, проведенная через центральную часть скопления точек, дает наиболее подходящую аппроксимацию наблюдаемого соотношения.
Можно измерить, как близко находятся наблюдения к прямой линии, которая лучше всего описывает их линейное соотношение путем вычисления коэффициента корреляции Пирсона, обычно называемого просто коэффициентом корреляции

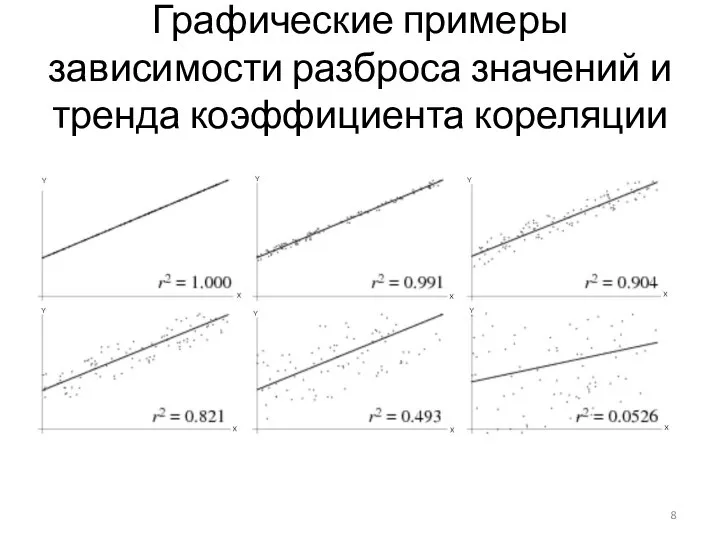
Графические примеры зависимости разброса значений и тренда коэффициента кореляции

Коэффициент корреляции Пирсона
Из свойств коэффициента корреляции r следует выделить:
- r изменяется в интервале от —1 до +1.
- знак r означает, увеличивается ли одна переменная по мере того, как увеличивается другая (положительный r), или уменьшается ли одна переменная по мере того, как увеличивается другая (отрицательный r).
- величина r величина указывает, как близко расположены точки к прямой линии.

Обработка и представление результатов исследования с помощью MS Excel

Температура кипения спиртов

Построение корреляционного графика
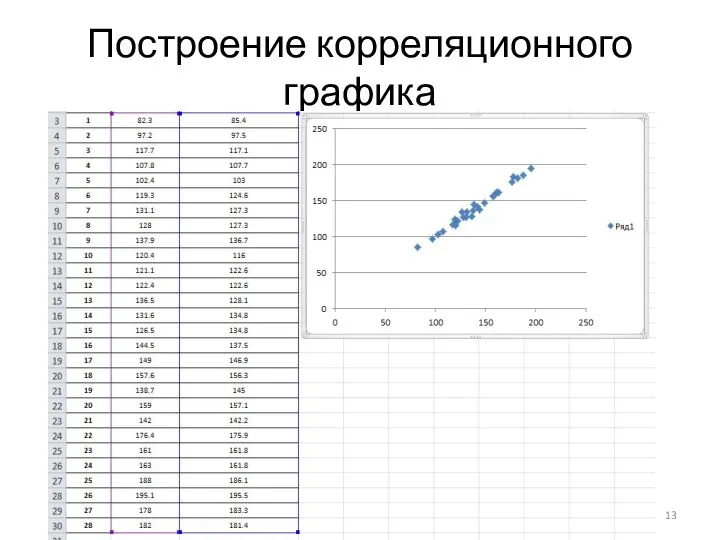
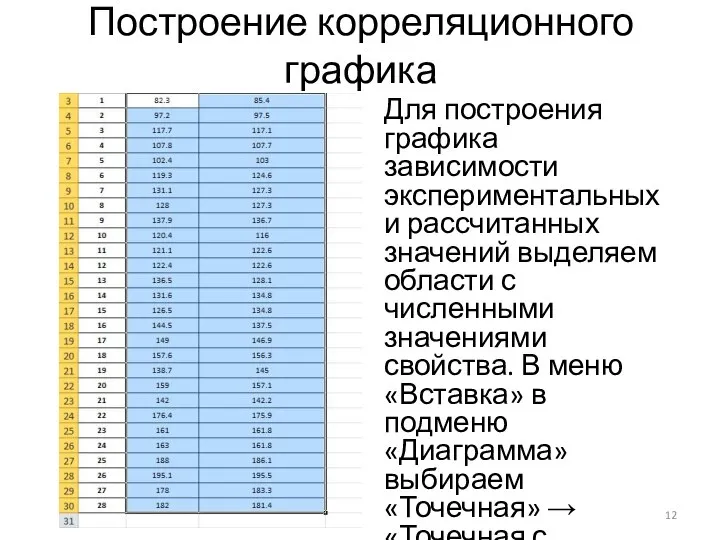
Для построения графика зависимости экспериментальных и рассчитанных значений выделяем области с численными значениями свойства. В меню «Вставка» в подменю «Диаграмма» выбираем «Точечная» → «Точечная с маркерами».

Построение корреляционного графика

Построение корреляционного графика
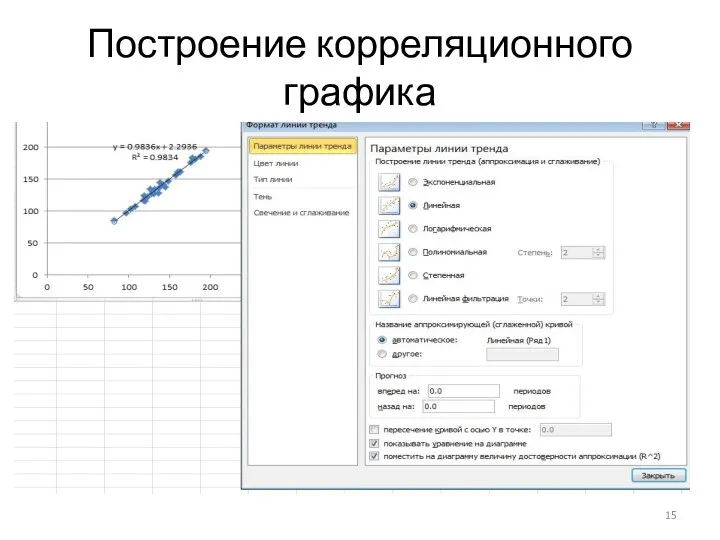
Выбрав на появившемся графике любой маркер, нажимаем правую кнопку мыши, и в открывшемся меню выбираем «Добавить линию тренда». В открывшемся окне «Формат линии тренда» нужно установить галочки напротив «Показать уравнение на диаграмме» и «Поместить на диаграмму величину достоверности аппроксимации (R^2)»

Построение корреляционного графика

Редактирование корреляционного графика
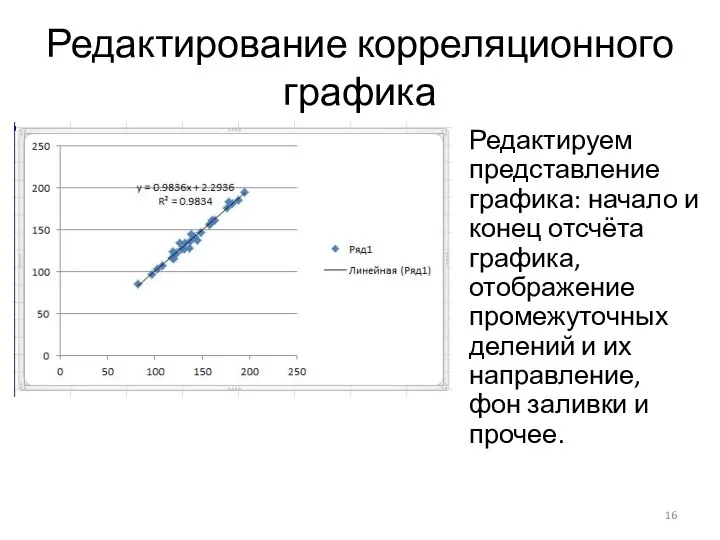
Редактируем представление графика: начало и конец отсчёта графика, отображение промежуточных делений и их направление, фон заливки и прочее.

Редактирование корреляционного графика
Удаляем «легенду»

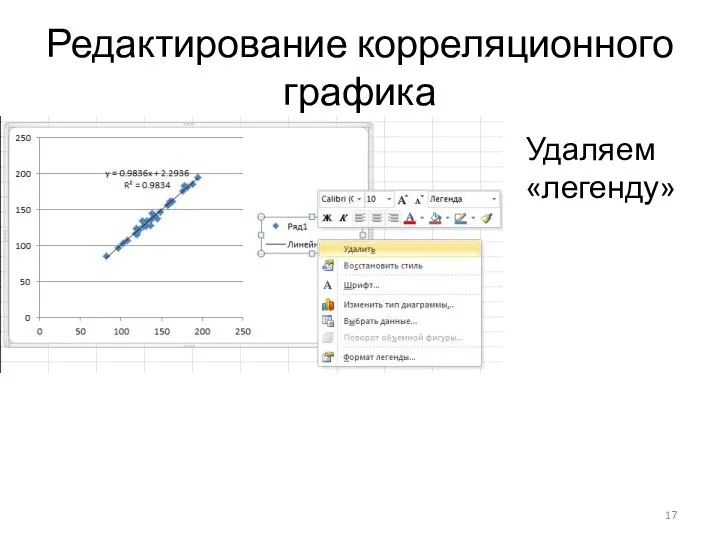
Редактирование корреляционного графика
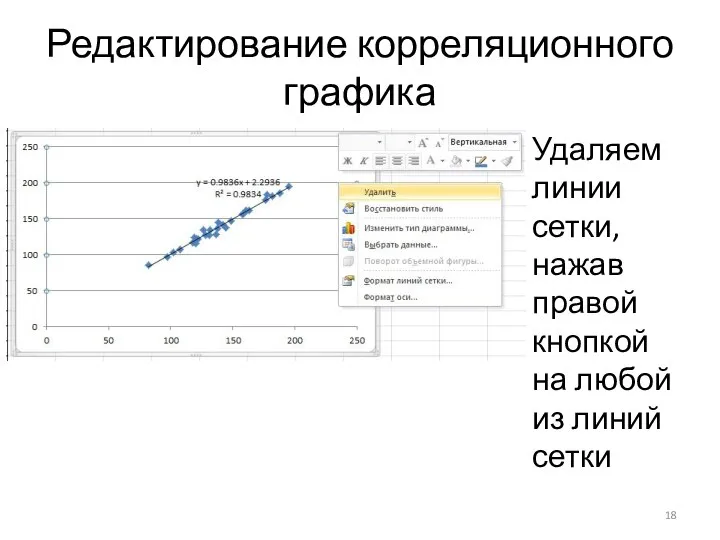
Удаляем линии сетки, нажав правой кнопкой на любой из линий сетки

Редактирование корреляционного графика
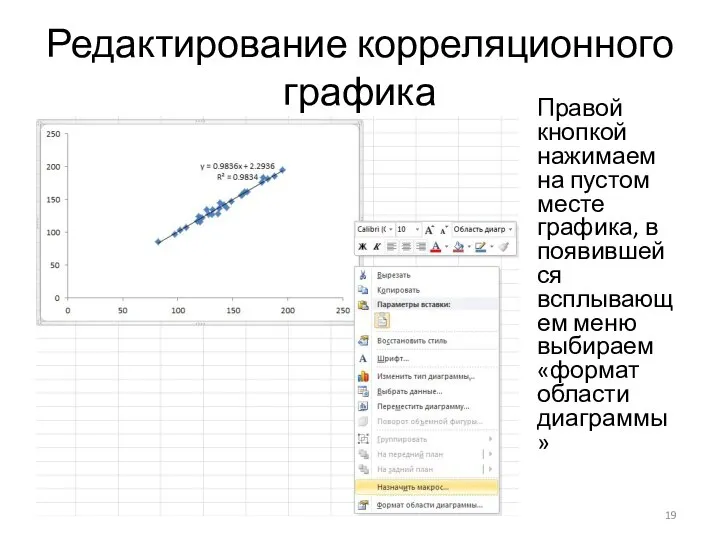
Правой кнопкой нажимаем на пустом месте графика, в появившейся всплывающем меню выбираем «формат области диаграммы»

Редактирование корреляционного графика
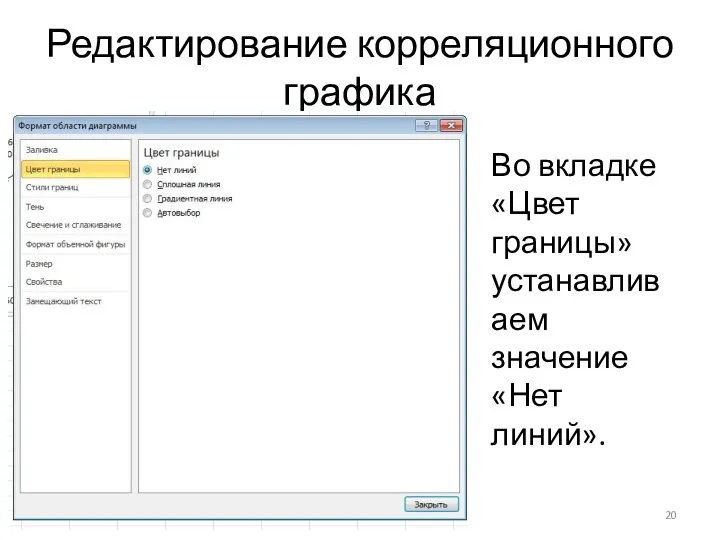
Во вкладке «Цвет границы» устанавливаем значение «Нет линий».

Редактирование корреляционного графика
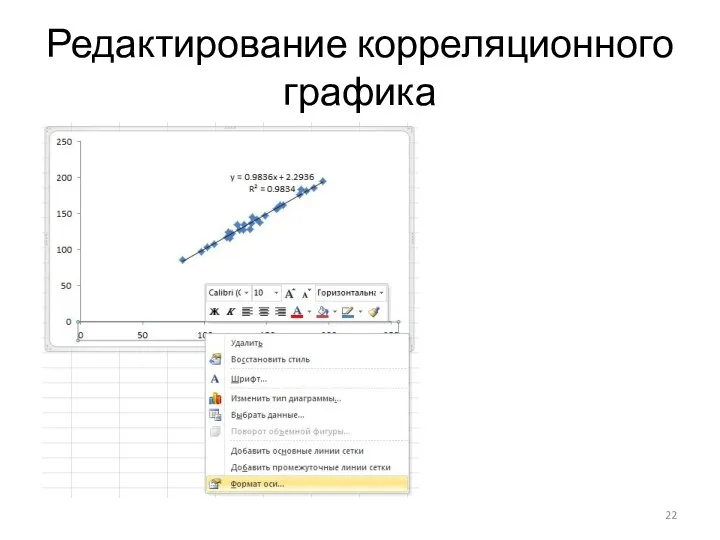
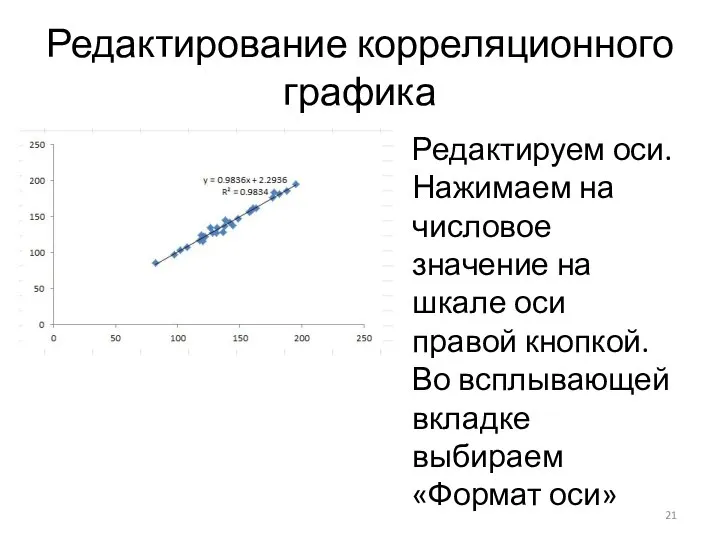
Редактируем оси. Нажимаем на числовое значение на шкале оси правой кнопкой. Во всплывающей вкладке выбираем «Формат оси»

Редактирование корреляционного графика

Редактирование корреляционного графика
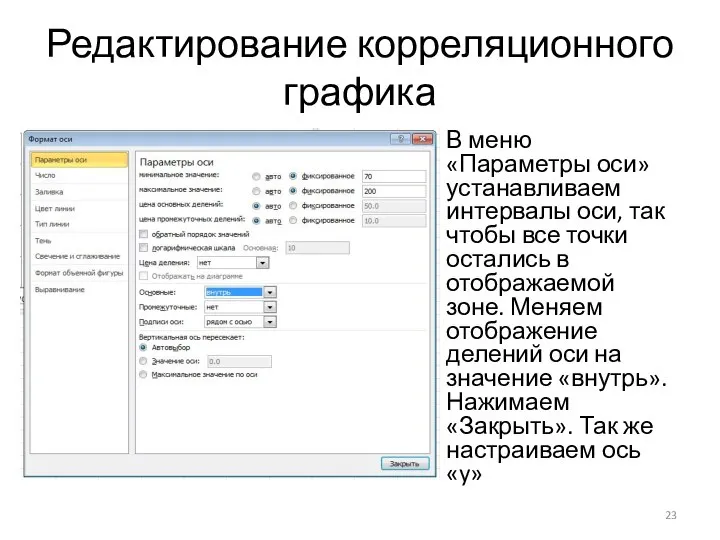
В меню «Параметры оси» устанавливаем интервалы оси, так чтобы все точки остались в отображаемой зоне. Меняем отображение делений оси на значение «внутрь». Нажимаем «Закрыть». Так же настраиваем ось «y»

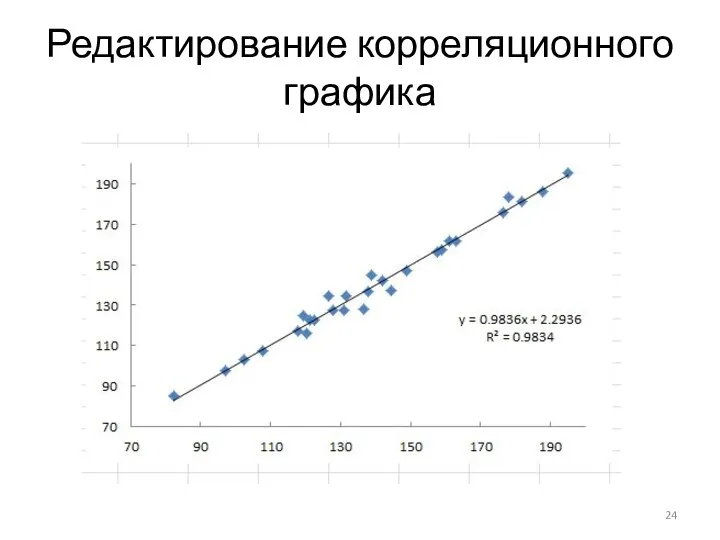
Редактирование корреляционного графика

Редактирование корреляционного графика
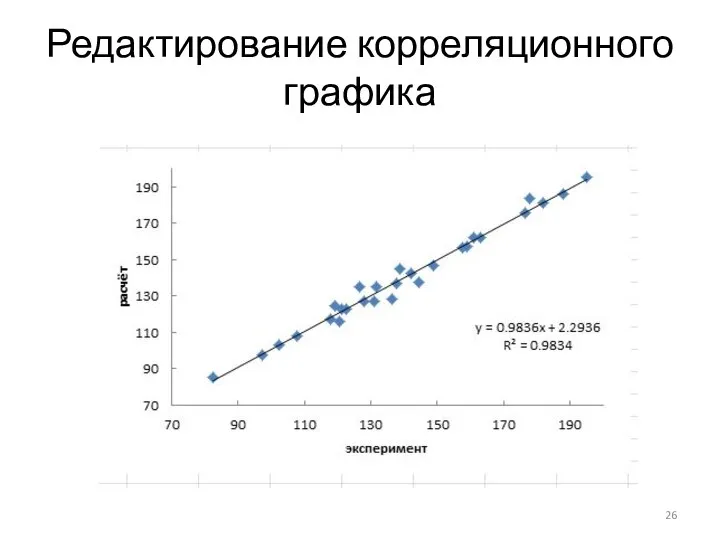
Подпишем оси. При активном режиме графика, на главной панели отображается меню «Работа с диаграммами», которое имеет 3 подменю. Выбираем подменю «Макет», вкладку «Название осей», во всплывающих меню выбираем нужные значения

Редактирование корреляционного графика

Построение гистограммы распределения частот ошибок
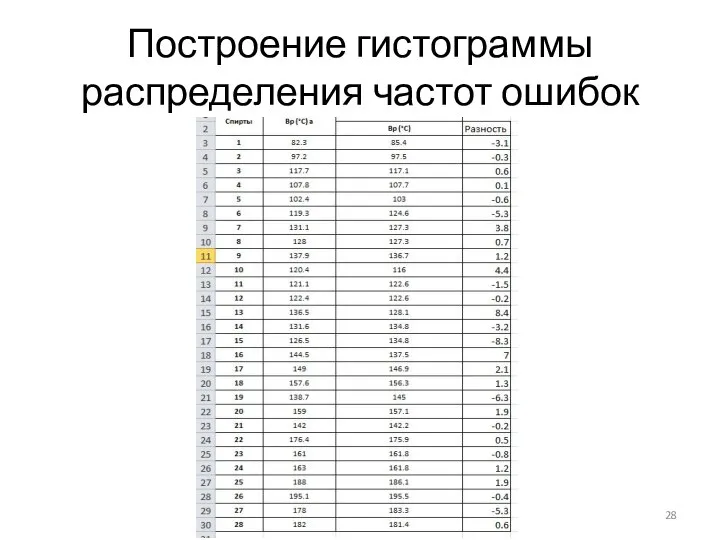
Находим разность между экспериментальными и расчетными данными, отнимая от экспериментальных значений рассчитанные.

Построение гистограммы распределения частот ошибок

Построение гистограммы распределения частот ошибок
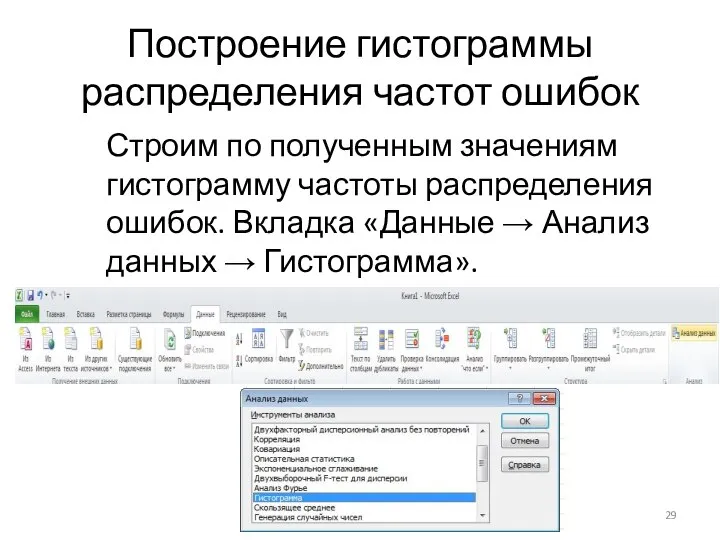
Строим по полученным значениям гистограмму частоты распределения ошибок. Вкладка «Данные → Анализ данных → Гистограмма».

Построение гистограммы распределения частот ошибок
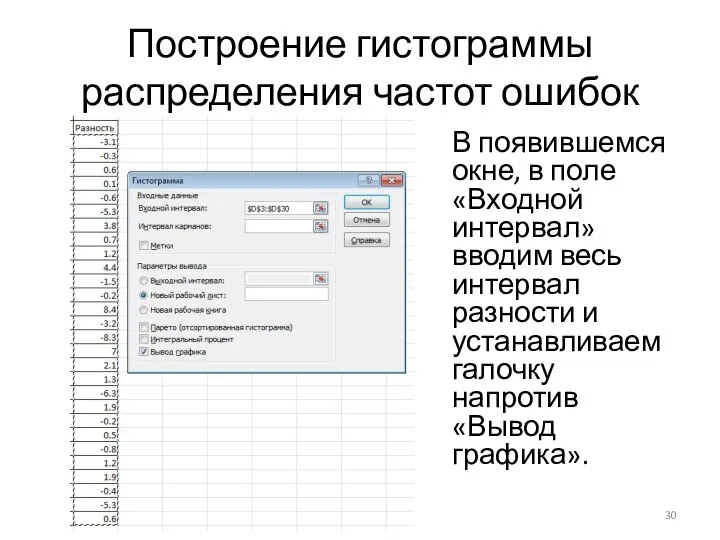
В появившемся окне, в поле «Входной интервал» вводим весь интервал разности и устанавливаем галочку напротив «Вывод графика».

Редактирование гистограммы распределения частот ошибок

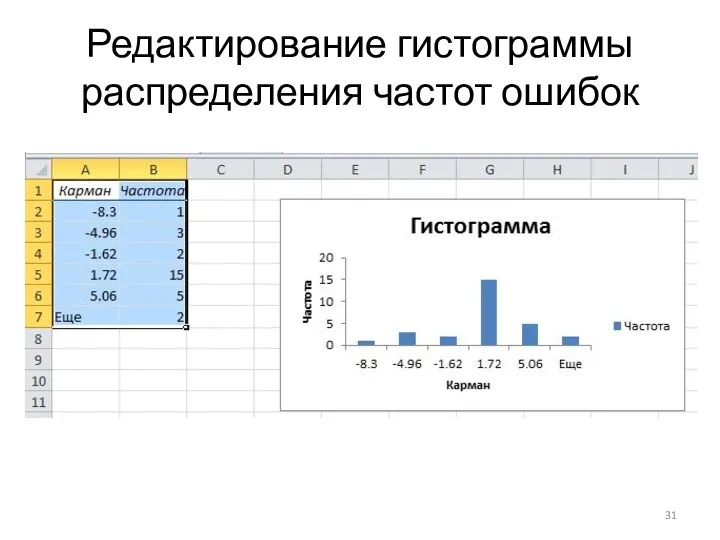
Редактирование гистограммы распределения частот ошибок
Редактируем гистограмму так же, как и корреляционный график:
Удаляем «легенду»
Удаляем название диаграммы «Гистограмма»
Удаляем цвет границы
Выставляем деления осей «Внутрь»

Редактирование гистограммы распределения частот ошибок
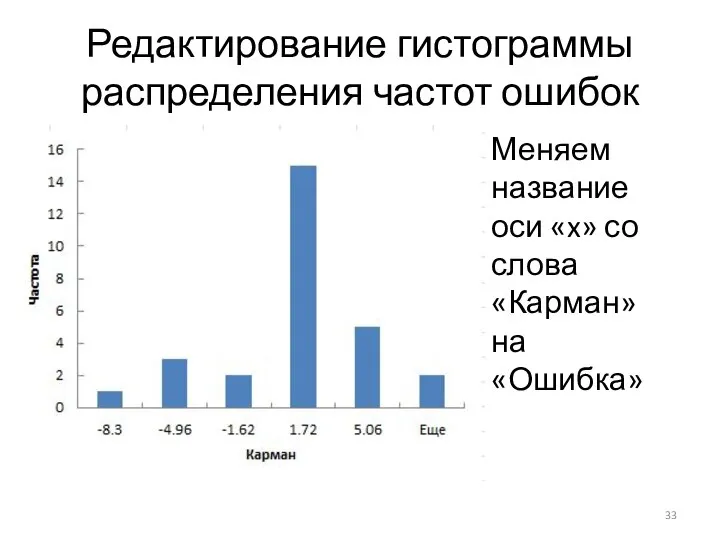
Меняем название оси «x» со слова «Карман» на «Ошибка»

Редактирование гистограммы распределения частот ошибок
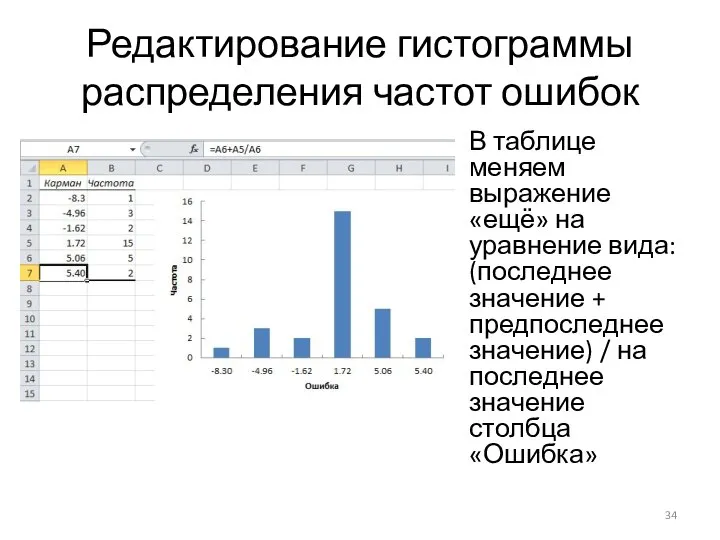
В таблице меняем выражение «ещё» на уравнение вида: (последнее значение + предпоследнее значение) / на последнее значение столбца «Ошибка»

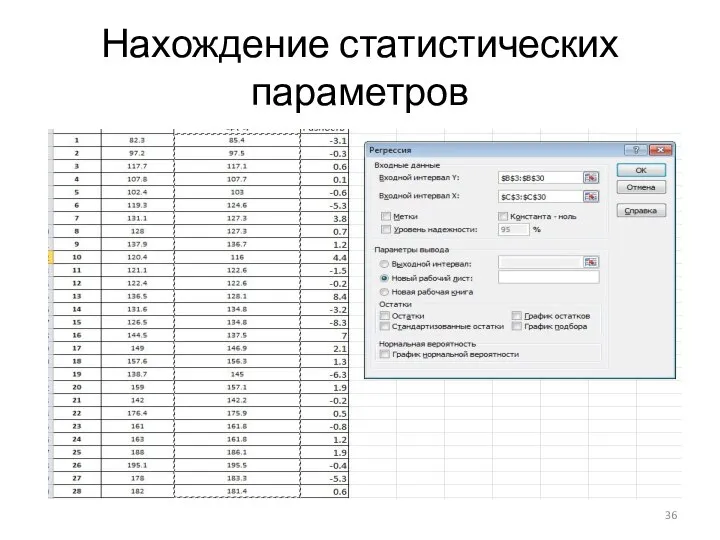
Нахождение статистических параметров
статистические параметры результатов исследования находятся, используя команду «регрессия» во вкладке «данные → анализ данных». В входном интервале Y указывается интервал значений экспериментальных данных, а в входном интервале X берётся интервал рассчитанных значений.

Нахождение статистических параметров

Статистические параметры исследования
Результатом является «таблица» в которой представлены следующие параметры «Множественный R» - коэффициент корреляции, «R-квадрат» - квадрат коэффициента корреляции, «Нормированный R-квадрат» - скорректированный индекс множественной детерминации, содержит поправку на число степеней свободы. «Стандартная ошибка» - погрешность измерения, оценка отклонения величины измеренного значения величины от её истинного значения. «Наблюдения» - число измерений