Транспортная задача как частный случай задач линейного программирования

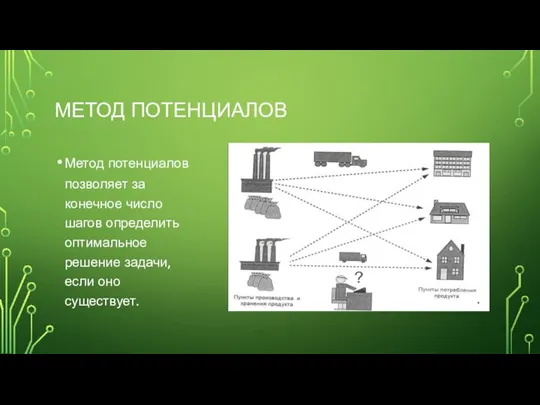
МЕТОД ПОТЕНЦИАЛОВ
Метод потенциалов позволяет за конечное число шагов определить оптимальное решение задачи, если оно существует.

Пусть есть первоначальное распределение по методу С-З угла.
30
20
5
35
20
1) Проверка на вырожденность
Таблица считается невырожденной(нормальной), если количество заполненных клеток = столбцы+строки-1
3+4-1=6
1
2
3
4
5
5≠6 – таблица вырожденная
От вырожденности избавляются выбирая пустую клетку с минимальными затратами и в нее делают фиктивную поставку = 0.
min
0

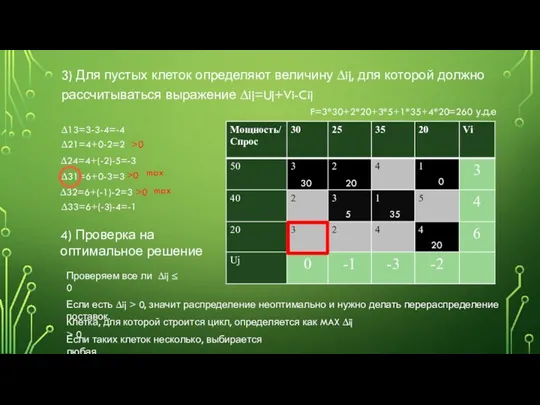
2) Для заполненных клеток рассчитываются потенциалы Uj и Vi такие, что Uj+Vi=Cij
30
20
5
35
20
0
В клетку U1 всегда ставится 0
0
3
-1
4
-3
-2
6

3) Для пустых клеток определяют величину ∆ij, для которой должно рассчитываться выражение ∆ij=Uj+Vi-Cij
30
20
5
35
20
0
∆13=3-3-4=-4
∆24=4+(-2)-5=-3
∆21=4+0-2=2
∆32=6+(-1)-2=3
∆31=6+0-3=3
∆33=6+(-3)-4=-1
4) Проверка на оптимальное решение
Проверяем все ли ∆ij ≤ 0
Если есть ∆ij > 0, значит распределение неоптимально и нужно делать перераспределение поставок.
>0
>0
>0
Клетка, для которой строится цикл, определяется как MAX ∆ij > 0
max
max
Если таких клеток несколько, выбирается любая
F=3*30+2*20+3*5+1*35+4*20=260 у.д.е

ЦИКЛ ПЕРЕРАСПРЕДЕЛЕНИЯ
Цикл перераспределения – это замкнутая ломаная линия, берущая начало в клетке, для которой строится цикл, все углы должны быть прямыми и находиться в заполненных клетках, в которых, чередуясь, ставятся +Х и –Х.
30
20
5
35
20
0
+Х
-Х
+Х
-Х
X=MIN(-x)
X=MIN(30;20)=20

После цикла перераспределения алгоритм нахождения оптимального решения начинается сначала
10
20
5
35
0
20
20
0
3
-1
4
-3
-2
3
1) Невырожденная
2)
3) ∆13=3-3-4=-4 ∆21=4+0-2=2
∆24=-2+4-5=-3
∆32=3-1-2=0
∆33=3-3-4=-4
∆34=3-2-4=-3
+Х
-Х
+Х
-Х
X=MIN(10;5)=5
F=3*10+2*20+1*20+1*35+3*5+3*20=200 у.д.е

30
20
5
35
20
0
5
25
0
35
20
20
0
3
-1
2
-1
-2
3
5
1) Невырожденная
2)
3) ∆13=3-1-4=-2
∆22=2-1-3=-2
∆24=-2+2-5=-5
∆32=3-1-2=0
∆33=3-1-4=-2
∆34=3-2-4=-3
F=3*5+2*25+1*20+2*5+1*35+3*20=190 у.д.е
Достигнуто оптимальное распределение, т.к. все ∆ij ≤ 0
Ответ: F=190 у.д.е