Цифровая схемотехника. Системы счисления. Логические элементы

Непозиционные и позиционные системы счисления
Для записи чисел используются специальные символы - цифры. Число – «слово», несет смысловую нагрузку – меру количества. Цифра – «буква», используется для записи чисел.
Непозиционные – значение цифр не зависят от их позиции в записи числа. Римская система записи десятичных чисел XXX - тридцать
Позиционные – значение цифр зависит от положения в записи числа. Арабская система записи десятичных чисел 30 – тридцать
В силу большего удобства при вычислениях позиционные системы счисления получили большее распространение. Далее мы будем рассматривать только эти системы счисления.

Основание систем счисления
Структурный элемент записи позиционного числа, который определяет значение цифры при записи называют разрядом(позицией, местом)
Количество цифр, используемых в позиционной системе счисления для записи всех чисел в пределах одного разряда, называется основанием системы счисления

Позиционная запись числа
Запишем произвольное число Z в позиционной системе счисления с основанием b
Эта запись для удобства вычисления может быть разложена в сумму вида:
Где:
n – количество разрядов числа (разрядность).
i – конкретный разряд , начиная с нулевого.

Распространенные основания систем счисления
Десятичная
Основание – 10
Числа - 0,1,2,3,4,5,6,7,8,9
Двоичная
Основание – 2
Числа – 0,1
Шестнадцатеричная
Основание – 16
Числа - 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F
Восьмеричная
Основание – 10
Числа - 0,1,2,3,4,5,6,7,8,9

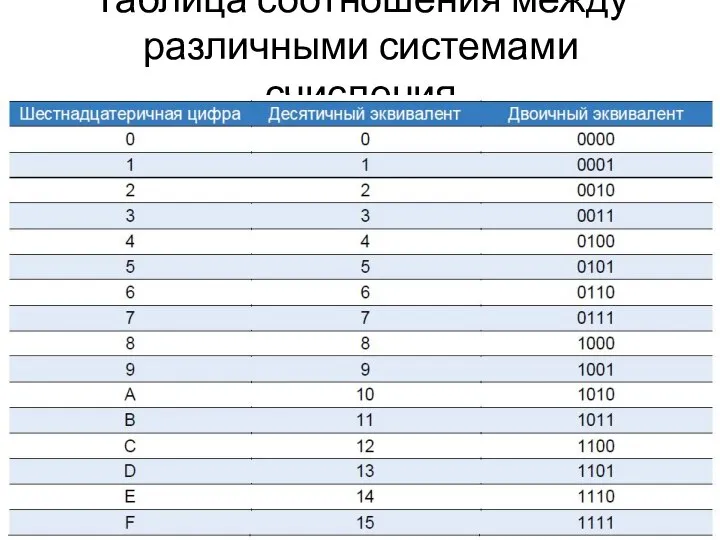
Таблица соотношения между различными системами счисления

Десятичная система счисления
Еще в начальной школе нас всех научили считать и выполнять различные арифметические операции в десятичной (decimal) системе счисления. Такая система использует десять арабских цифр: 0, 1, 2, 3, 4,5, 6, 7, 8, 9 – столько же, сколько у нас пальцев на руках. Числа больше 9 записываются в виде строки цифр. Причем, цифра, находящаяся в каждой последующей позиции такой строки, начиная с крайней правой цифры, имеет «вес», в десять раз превышающий «вес» цифры, находящейся в предыдущей позиции. Именно поэтому десятичную систему счисления называют системой по основанию (base) 10. Справа налево «вес» каждой позиции увеличивается следующим образом: 1, 10, 100, 1000 и т.д. Позицию, которую цифра занимает в строке десятичного числа, называют разрядом.
Чтобы избежать недоразумений при одновременной работе с более чем одной системой счисления, основание системы обычно указывается путем добавления цифры позади и чуть ниже основного числа. Рис. показывает, для примера, как десятичное число 9742 может быть записано в виде суммы цифр, составляющих это число, умноженных на «вес» разряда, соответствующего каждой конкретной цифре.
N-разрядное десятичное число может представлять одну из 10N цифровых комбинаций: 0, 1, 2, 3, … 10N − 1. Это называется диапазоном N-разрядного числа. Десятичное число, состоящее из трех цифр (разрядов), например, представляет одну из 1000 возможных цифровых комбинаций в диапазоне от 0 до 999.

Двоичная система счисления
Одиночный бит может принимать одно из двух значений, 0 или 1. Несколько битов, соединенных в одной строке, образуют двоичное (binary) число. Каждая последующая позиция в двоичной строке имеет вдвое больший «вес», чем предыдущая позиция, так что двоичная система счисления – это система по основанию 2.
В двоичном числе «вес» каждой позиции увеличивается (так же, как и в десятичном – справа налево) следующим образом: 1, 2, 4, 8, 16, 32, 64, 128, 256, 512,1024, 2048, 4096, 8192, 16384, 32768, 65536 и т.д.
Работая с двоичными числами, очень полезно для сохранения времени запомнить значения степеней двойки до 216.

Преобразование числа из двоичной системы в десятичную
Все просто. «В лоб» представляем запись числа в виде поразрядной суммы произведения цифры в разряде на вес разряда, как и предписывает нам теория позиционной записи чисел

Преобразование числа из десятичной системы в двоичную
Преобразуем десятичное число 8410 в двоичное.
Определим, что должно стоять в каждой позиции двоичного результата: 1 или 0. Вы можете делать это, начиная с левой или правой позиции.
Если начать слева, найдите наибольшую степень 2, меньше или равную заданному числу (в Примере такая степень – это 64). 84 > 64, поэтому ставим 1 в позиции, соответствующей 64. Остается 84–64 = 20, 20 < 32, так что в позиции 32 надо поставить 0, 20 > 16, поэтому в позиции 16 ставим 1. Остается 20 –16 = 4. 4 < 8, поэтому 0 в позиции 8. 4 ≥ 4 – ставим 1 в позицию 4. 4–4 = 0, поэтому будут 0 в позициях 2 и 1. Собрав все вместе, получаем 8410 = 10101002.
Если начать справа, будем последовательно делить исходное число на 2. Остаток идет в очередную позицию. 84/2 = 42, поэтому 0 в самой правой позиции. 42/2 = 21, 0 во вторую позицию. 21/2 = 10, остаток 1 идет в позицию, соответствующую 4. 10/2 = 5, поэтому 0 в позицию, соответствующую 8. 5/2 = 2, остаток 1 в позицию 16. 2/2 = 1, 0 в 32 позицию. Наконец, 1/2 = 0 с остатком 1, который идет в позицию 64. Снова, 8410 = 10101002

Шестнадцатеричная система счисления
Использование длинных двоичных чисел для записи и выполнения математических расчетов на бумаге утомительно и чревато ошибками. Однако длинное двоичное число можно разбить на группы по четыре бита, каждая из которых представляет одну из 24 = 16 цифровых комбинаций. Именно поэтому зачастую бывает удобнее использовать для работы систему счисления по основанию 16, называемую шестнадцатеричной (hexadecimal). Для записи шестнадцатеричных чисел используются цифры от 0 до 9 и буквы от A до F. В шестнадцатеричном числе «вес» каждой позиции меняется следующим образом: 1, 16, 162 (или 256), 163 (или 4096) и т.д.
Интересно, что термин hexadecimal (шестнадцатеричный) введен в научный обиход корпорацией IBM в 1963 году и является комбинацией греческого слова hexi (шесть) и латинского decem (десять). Правильнее было бы использовать латинское же слово sexa (шесть), но научное сообщество сочло, что термин sexadecimal воспринимался бы несколько неоднозначно.

Преобразование шестнадцатеричного числа в двоичное и десятичное
Преобразовать шестнадцатеричное число 2ЕD16 в двоичное и десятичное.
Преобразование шестнадцатеричного числа в двоичное и обратно – очень простое, так как каждая шестнадцатеричная цифра прямо соответствует 4-разрядному двоичному числу. 216 = 00102, Е16 = 11102 и D16 = 11012, так что 2ED16 = 0010111011012
Преобразование в десятичную систему счисления требует арифметики, основанной на поразрядном разложении в сумму, и показано ниже.

Преобразование двоичного числа в десятичное
Преобразовать двоичное число 11110102 в шестнадцатеричное.
Решение. Повторим еще раз, это просто. Начинаем справа.
4 наименее значимых бита 10102 = А16
Следующие биты 1112 = 716
Отсюда 11110102 = 7А16

Преобразование десятичного числа в шестнадцатеричное и двоичное
Преобразовать десятичное число 33310 в шестнадцатеричное и двоичное.
Как и в случае преобразования десятичного числа в двоичное, можно начать как слева, так и справа. Если начать слева, найдите наибольшую степень шестнадцати, меньшую или равную заданному числу (в нашем случае это 162 = 256). Число 256 содержится в числе 333 только один раз, поэтому в позицию с «весом» 256 мы записываем единицу. Остается число 333–256=77. Число 16 содержится в числе 77 четыре раза, поэтому в позицию с «весом» 16 записываем четверку. Остается 77 – 16 × 4 = 13. 1310 = D16, поэтому в позицию с «весом» 1 записываем цифру D. Итак, 33310 = 14D16, это число легко преобразовать в двоичное, как мы показали ранее: 14D16 = 1010011012
Если начинать справа, будем повторять деление на 16. Каждый раз остаток идет в очередную колонку. 333/16 = 20 с остатком 1310 = D16, который идет в самую правую позицию. 20/16 = 1 с остатком 4, который идет в позицию с «весом» 16. 1/16 = 0 с остатком 1, который идет в позицию с «весом» 256. В результате Опять получаем 14D16

Байт, полубайт, 64,32,16,8 бит
Группа из восьми битов называется байт (byte). Байт представляет 28 = 256 цифровых комбинаций. Цифровые устройства обычно оперируют байтами, а не битами. Группа из четырех битов (половина байта) называется полубайт (nibble). Полубайт представляет 24 = 16 цифровых комбинаций. Одна шестнадцатеричная цифра занимает один полубайт, а две шестнадцатеричные цифры – один байт. В настоящее время полубайты уже не находят широкого применения, однако этот термин все же стоит знать, да и звучит он забавно (в английском языке nibble означает откусывать что-либо маленькими кусочками).
Цифровые устройства обрабатывает данные не целиком, а небольшими блоками, называемыми словами. Размер слова (word) не является величиной, установленной раз и навсегда, а определяется архитектурой каждого конкретного устройства. Например, в настоящее время большинство компьютеров использует 64-битные процессоры. Такие процессоры обрабатывают информацию блоками (словами) длиной 64 бита. А еще не так давно верхом совершенства считались компьютеры, обрабатывающие информацию словами длиной 32 бита. Интересно, что и сегодня наиболее простые микропроцессоры и особенно те, что управляют работой таких бытовых устройств, как, например, тостеры или микроволновые печи, используют слова длиной 8 бит.
В рамках одной группы битов конечный бит, находящийся на одном конце этой группы (обычно правом), называется наименее значимым битом (least significant bit, lsb), или просто младшим битом, а бит на другом конце группы называется наиболее значимым битом (most significant bit, msb), или старшим битом. Рис. A демонстрирует наименее и наиболее значимые биты в случае 6-битного двоичного числа. Аналогичным образом, внутри одного слова можно выделить наименее значимый байт (least significant byte, LSB), или младший байт, и наиболее значимый байт (most significant byte, MSB), или старший байт. Рис. B показывает, как это делается в случае 4-байтного числа, записанного восемью шестнадцатеричными цифрами.

Сложение двоичных чисел
Сложение двоичных чисел производится так же, как и сложение десятичных, с той лишь разницей, что двоичное сложение выполнить гораздо проще (см. Рис). Как и при сложении десятичных чисел, если сумма двух чисел превышает значение, помещающееся в один разряд, мы переносим 1 в следующий разряд. На Рис. сравнения показано сложение десятичных и двоичных чисел. В крайней правой колонке на Рис. a складываются числа 7 и 9. Сумма 7 + 9 = 16, что превышает 9, а значит, больше того, что может вместить один десятичный разряд. Поэтому мы записываем в первый разряд 6 (первая колонка), и переносим 10 в следующий разряд (вторая колонка) как 1. Аналогичным же образом при сложении двоичных чисел, если сумма двух чисел превышает 1, мы переносим 2 в следующий разряд как 1. В правой колонке на Рис. b, например, сумма 1 + 1 = 210 = 102, что не может уместиться в одном двоичном разряде. Поэтому мы записываем 0 в первом разряде (первая колонка) и 1 в следующем разряде (вторая колонка). Во второй колонке опять складываются 1 и 1 и еще добавляется 1, перенесенная сюда после сложения чисел в первой колонке. Сумма 1 + 1 + 1 = 310 = 112. Мы записываем 1 в первый разряд (вторая колонка) и снова добавляем 1 в следующий разряд (третья колонка). По очевидной причине бит, добавленный в соседний разряд (колонку), называется битом переноса (carry bit).

Переполнение
Цифровые системы обычно оперируют числами с заранее определенным и фиксированным количеством разрядов. Ситуацию, когда результат сложения превышает выделенное для него количество разрядов, называют переполнением (overflow). Четырехбитная ячейка памяти, например, может сохранять значения в диапазоне [0, 15]. Такая ячейка переполняется, если результат сложения превышает число 15. В этом случае дополнительный пятый бит отбрасывается, а результат, оставшийся в четырех битах, будет ошибочным. Переполнение можно обнаружить, если следить за переносом бита из наиболее значимого разряда двоичного числа (повторяем предыдущийрисунок), из наиболее левой колонки

Знак двоичного числа
До сих пор мы рассматривали двоичные числа без знака (unsigned) – то есть только положительные числа. Часто, однако, для вычислений требуются как положительные, так и отрицательные числа, а это значит, что для знака двоичного числа нам потребуется дополнительный разряд. Существует несколько способов представления двоичных чисел со знаком (signed). Наиболее широко применяются два:
Прямой Код (Sign/Magnitude)
Дополнительный Код (Two’s Complement).

Прямой код
Представление отрицательных двоичных с использованием прямого кода интуитивно покажется вам наиболее привлекательным, поскольку совпадает с привычным способом записи отрицательных чисел, когда сначала идет знак минус, а затем абсолютное значение числа. Двоичное число, состоящее из N битов и записанное в прямом коде, использует наиболее значимый бит для знака, а остальные N−1 бита для записи абсолютного значения этого числа. Если наиболее значимый бит 0, то число положительное. Если наиболее значимый бит 1, то число отрицательное.
Пример Запишем числа 5 и –5 как четырехбитовые числа в прямом коде Оба числа имеют абсолютную величину 510 = 1012. Таким образом, 510 = 01012 и –510 = 11012.
К сожалению, стандартный способ сложения не работает в случае двоичных чисел со знаком, записанных в прямом коде. Например, складывая −510 + 510 привычным способом, получаем 11012 + 01012 = 100102. Что, естественно, есть полный абсурд.
Другой несколько странной особенностью прямого кода является наличие +0 и −0, причем оба этих числа соответствуют одному нулю. Нетрудно предположить, что представление одной и той же величины двумя различными способами чревато ошибками.
Двоичная переменная длиной N битов в прямом коде может представлять число в диапазоне [−2N−1 + 1, 2N −1 − 1].

Дополнительный код
Двоичные числа, записанные с использованием дополнительного кода, и двоичные числа без знака идентичны, за исключением того, что в случае дополнительного кода вес наиболее значимого бита −2N−1 вместо 2N−1, как в случае двоичного числа без знака. Дополнительный код гарантирует однозначное представление нуля, допускает сложение чисел по привычной схеме, а значит, избавлен от недостатков прямого кода.
В случае дополнительного кода нулевое значение представлено нулями во всех разрядах двоичного числа: 00…0002.
Максимальное положительное значение представлено нулем в наиболее значимом разряде и единицами во всех других разрядах двоичного числа: 01…1112 = 2N−1 − 1.
Максимальное отрицательное значение имеет единицу в наиболее значимом разряде и нули во всех остальных разрядах: 10…0002 = −2N−1.
Отрицательная единица представлена единицами во всех разрядах двоичного числа: 11…1112.
Обратите внимание на то, что наиболее значимый разряд у всех положительных чисел – это «0», в то время как у отрицательных чисел – это «1», то есть наиболее значимый бит дополнительного кода можно рассматривать как аналог знакового бита прямого кода. Однако на этом сходство кончается, поскольку остальные биты дополнительного кода интерпретируются не так, как биты прямого кода.
В случае дополнительного кода, знак отрицательного двоичного числа изменяется на противоположный путем выполнения специальной операции, называемой дополнением до двух (taking the two’s complement). Суть этой операции заключается в том, что инвертируются все биты этого числа, а затем к значению наименее значимого бита прибавляется 1. Подобная операция позволяет найти двоичное представление отрицательного числа или определить его абсолютное значение.

Отрицательные числа в дополнительном коде
Найдем представление −210 как 4-битового числа в дополнительном коде.
начнем с +210 = 00102. Для получения −210 инвертируем биты и добавим единицу. Инвертируя 00102, получим 11012. 11012 + 1 = 11102.
Итак, −210 равно 11102.
Найдем десятичное значение числа 10012 в дополнительном коде.
Число 10012 имеет старшую 1, поэтому оно должно быть отрицательным.
Чтобы найти его модуль, инвертируем все биты и добавляем 1.
Инвертируя 10012, получим 01102. 01102 + 1 = 01112 = 710.
Отсюда, 10012 = −710.

Арифметические операции с числами в дополнительным кодом
СЛОЖЕНИЕ ЧИСЕЛ, ПРЕДСТАВЛЕННЫХ В ДОПОЛНИТЕЛЬНОМ КОДЕ
Неоспоримым преимуществом дополнительного кода является то, что привычный способ сложения работает как в случае положительных, так и отрицательных чисел. Напомним, однако, что при сложении N-битных чисел N-ный бит (т.е. N + 1-й бит результата) не переносится.
Вычислить (a) −210 + 110 и (b) −710 + 710 с помощью чисел в дополнительном коде
(a) −210 + 110 = 11102 + 00012 = 11112 = −110.
(b) −710 + 710 = 10012 + 01112 = 100002. Пятый бит отбрасывается, оставляя правильный 4-битовый результат 00002.
ВЫЧИТАНИЕ ЧИСЕЛ В ДОПОЛНИТЕЛЬНОМ КОДЕ
Вычитание одного двоичного числа из другого осуществляется путем преобразования вычитаемого в дополнительный код и последующего его сложения с уменьшаемым.
Вычислить (a) 510 − 310 и (b) 310 − 510, используя 4-разрядные числа в дополнительном коде.
(a) 310 = 00112. Вычисляя его дополнительный код, получим −310 = 11012. Теперь сложим 510 + (−310) = 01012 + 11012 = 00102 = 210. Отметим, что перенос из наиболее значимой позиции сбрасывается, поскольку результат записывается в четырех битах.
b) Вычисляя дополнительный код от 510, получим −510 = 10112. Теперь сложим 310 + (−510) = 00112 + 10112 = 11102 = −210.

Сложение чисел в дополнительном коде с переполнением
В случае дополнительного кода сложение двух положительных или отрицательных N-битовых чисел может привести к переполнению, если результат будет больше, чем 2N−1 – 1, или меньше, чем −2N−1. Сложение положительного и отрицательного числа, напротив, никогда не приводит к переполнению.
В отличие от двоичного числа без знака перенос наиболее значимого бита не является признаком переполнения. Вместо этого индикатором переполнения является ситуация, когда после сложения двух чисел с одинаковым знаком знаковый бит суммы не совпадает со знаковыми битами слагаемых.
В случае необходимости увеличения количества битов произвольного числа, записанного в дополнительном коде, значение знакового бита должно быть скопировано в наиболее значимые разряды модифицированного числа. Эта операция называется знаковым расширением (sign extension). Например, числа 3 и −3 записываются в 4-битном дополнительном коде как 0011 и 1101 соответственно. Если мы увеличиваем число разрядов до семи битов, мы должны скопировать знаковый бит в три наиболее значимых бита модифицированного числа, что дает 0000011 и 1111101.

Цифровая схемотехника
3. Логические элементы

Джордж Буль
Джордж Буль родился в семье небогатого ремесленника. Родители Джорджа не могли оплатить его формального образования, поэтому он осваивал математику самоучкой. Несмотря на это, Булю удалось стать преподавателем Королевского колледжа в Ирландии.
В 1854 году Джордж Буль написал свою работу «Исследование законов мышления», которая впервые ввела в научный оборот двоичные переменные, а также три основных логических оператора И, ИЛИ, НЕ (AND, OR, NOT).

Логические элементы (вентили)
Теперь, когда мы знаем, как использовать бинарные переменные для представления информации, рассмотрим цифровые системы, способные выполнять различные операции с этими переменными. Логические вентили (logic gates) – это простейшие цифровые схемы, получающие один или более двоичных сигналов на входе и производящие новый двоичный сигнал на выходе. При графическом изображении логических вентилей для обозначения одного или нескольких входных сигналов и выходного сигнала используются специальные символы. Если смотреть на изображение логического элемента, то входные сигналы обычно размещаются слева (или сверху), а выходные сигналы – справа (или снизу). Разработчики цифровых систем обычно используют первые буквы латинского алфавита для обозначения входных сигналов и латинскую букву Y для обозначения выходного сигнала. Взаимосвязь между входными сигналами и выходным сигналом логического вентиля может быть описана с помощью таблицы истинности (truth table) или уравнением Булевой логики. Слева в таблице истинности представлены значения входных сигналов, а справа – значение соответствующего выходного сигнала. Каждая строка в такой таблице соответствует одной из возможных комбинаций входных сигналов. Уравнение Булевой логики – это математическое выражение, описывающее логический элемент с помощью двоичных переменных.

Логический элемент НЕ
Логический вентиль НЕ (NOT gate) имеет один вход A и один выход Y, как показано на Рис. Причем выходной сигнал Y – это сигнал, обратный входному сигналу A, или, как еще говорят, инвертированный A (inversed A). Если сигнал на входе A – это ЛОЖЬ, то сигнал на выходе Y будет ИСТИНА. Таблица истинности и уравнение Булевой логики на Рис. суммируют эту связь входного и выходного сигналов. В уравнении Булевой логики линия над обозначением сигнала читается как «не», то есть математическое выражение Y = A¯ произносится как «Y равняется не A».
Именно поэтому логический вентиль НЕ также называют инвертором (inverter).
Для обозначения логического вентиля НЕ используют и другие способы записи, включая: Y = A', Y = ¬A, Y = !A и Y = ~A. Не удивляйтесь, если в научной и технической литературе вы столкнетесь и с другими обозначениями.

Буфер
Буфер просто копирует входной сигнал на выход. Если рассматривать буфер как часть логической схемы, то такой элемент ничем не отличается от простого провода и может показаться бесполезным.
Вместе с тем, на аналоговом уровне буфер может обеспечить характеристики, необходимые для нормального функционирования разрабатываемого устройства.
Буфер, например, необходим для передачи большого тока электродвигателю или для быстрой передачи сигнала сразу нескольким логическим элементам.
Это еще один пример, доказывающий необходимость рассмотрения любой системы с нескольких уровней абстракции, если мы хотим в полной мере понять эту систему. Рассмотрение буфера только с позиции цифрового уровня абстракции не позволяет нам разглядеть его реальную функцию.

Логический элемент И
Логические вентили с двумя входными сигналами гораздо интереснее, чем вентиль НЕ и буфер.
Логический вентиль И (AND gate), показанный на Рис. выдает значение ИСТИНА на выход Y исключительно только если оба входных сигнала A и B имеют значение ИСТИНА. В противном случае выходной сигнал Y имеет значение ЛОЖЬ.
В используемом нами соглашении входные сигналы перечислены в порядке 00, 01, 10, 11, как в случае подсчета в двоичной системе счисления.
Уравнение Булевой логики для логического элемента И может быть записано несколькими способами: Y = A • B, Y = AB, или Y = A ∩ B. Символ ∩ читается как «пересечение» и больше других нравится специалистам в математической логике.
Однако, мы предпочтем использовать выражение Y = AB, которое звучит как «Y равно A и B», просто потому, что мы достаточно ленивы, чтобы выбрать то, что короче.

Логический элемент ИЛИ
Логический вентиль ИЛИ (OR gate), показанный на Рис., выдаёт значение ИСТИНА на выход Y, если хотя бы один из двух входных сигналов A или B имеет значение ИСТИНА.
Уравнение Булевой логики для логического элемента ИЛИ записывается как Y = A + B или Y = A U B.
Символ U читается как «объединение» и опять же больше всего нравится математикам. Разработчики цифровых систем обычно пользуются простым символом +.
Математическое выражение Y = A + B звучит «Y равно A или B».

Другие логические элементы
Вы видите другие широко распространенные логические вентили с двумя входными сигналами.
Добавление кружка на выходе любого логического вентиля превращает этот вентиль в ему противоположный – то есть инвертирует его. Таким образом, например, из вентиля И получается вентиль И-НЕ (NAND gate). Значение выходного сигнала Y вентиля И-НЕ будет ИСТИНА до тех пор, пока оба входных сигнала А и В не примут значение ИСТИНА.
Точно так же из логического вентиля ИЛИ получается вентиль ИЛИ-НЕ (NOR gate). Его выходной сигнал Y будет ИСТИНА в том случае, если ни один из входных сигналов, ни А ни B, не имеет значение ИСТИНА.
Исключающее ИЛИ с количеством входов равным N (N-input XOR gate) иногда еще называют элементом контроля по чётности (parity gate). Такой вентиль выдает на выход сигнал ИСТИНА, если нечетное количество входных сигналов имеет значение ИСТИНА. Как и в случае элемента с двумя входными сигналами, комбинации сигналов для элемента с N входами перечислены в логической таблице в порядке подсчета в двоичной системе счисления.