Введение в логику

Основные вопросы
Основные понятия логики
Предмет логики
Формы мышления
Понятие
Умозаключение
Высказывание
Алгебра высказываний
Основные логические операции
Таблицы истинности
Законы логики
Упрощение логических выражений
Решение логических задач
Логические основы работы компьютера

Предмет логики
Логика – это наука о формах и способах мышления.
Логика изучает:
Формы мышления
Способы мышления

Формы мышления
Понятие
Умозаключение
Высказывание

Понятие
Понятие- это форма человеческого мышления, где фиксируются основные, существенные признаки объекта.
Любое понятие состоит из двух составляющих:
объёма понятия и
содержания понятия.

Понятие
Объем понятия- это совокупность (множество) предметов, на которое оно распространяется.
Содержание понятия- это совокупность основных, существенных признаков объекта.

Понятие
Пример
Файл- это поименованная область на внешнем носителе информации.
Объём этого понятия- множество файлов (компьютерных).
Содержание состоит из двух существенных признаков:
поименованная область и
на внешнем носителе информации.

Умозаключение
Умозаключение- это форма мышления, с помощью которой из одного или нескольких суждений (посылок) может быть получено новое суждение (заключение).

Высказывание
Высказывание- это форма мышления, в которой что-либо утверждается или отрицается о свойствах реальных объектов и отношениях между ними.
Высказывание может быть либо истинным, либо ложным.

Алгебра высказываний
Высказывания могут быть простыми или составными.
2+2=4 – это пример простого высказывания.
Составные высказывания состоят из простых высказываний и логических операций.
“На улице солнечно и у меня хорошее настроение.” – это пример составного высказывания.
Алгебра высказываний определяет истинность или ложность составных высказываний.

Алгебра высказываний
Математический аппарат логики:
Вводятся вместо простых высказываний логические переменные: А, В, С и т.д.
Значения высказываний обозначаются следующим образом:
истина- 1
ложь- 0.

Логические операции

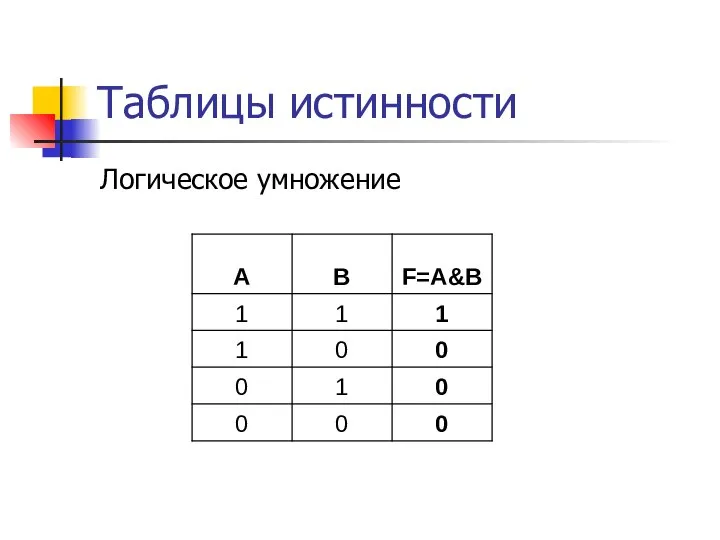
Таблицы истинности
Логическое умножение

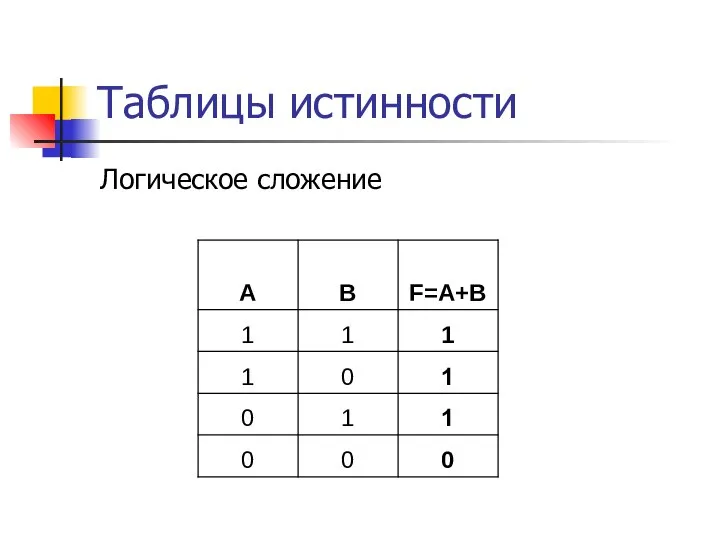
Таблицы истинности
Логическое сложение

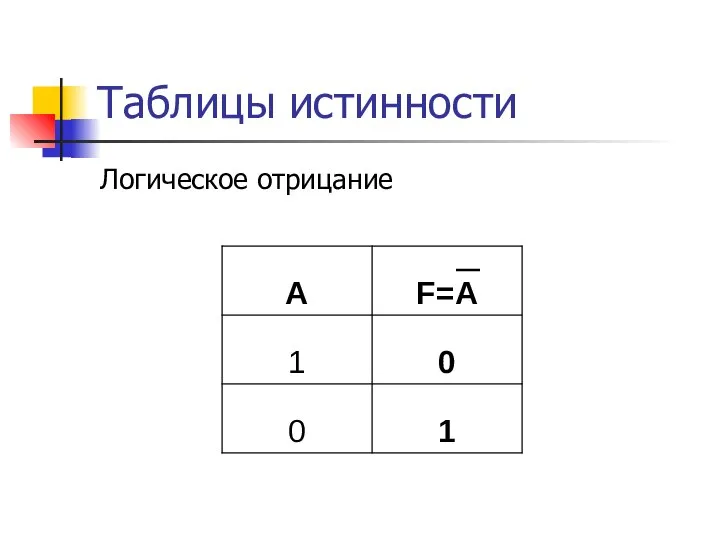
Таблицы истинности
Логическое отрицание

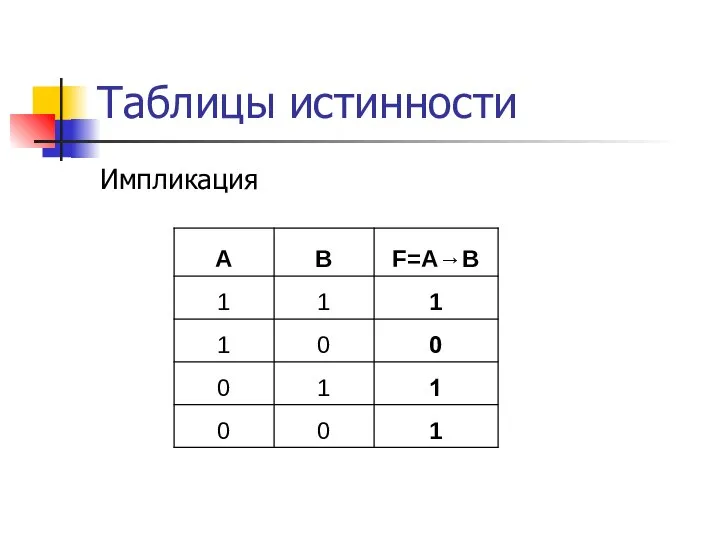
Таблицы истинности
Импликация

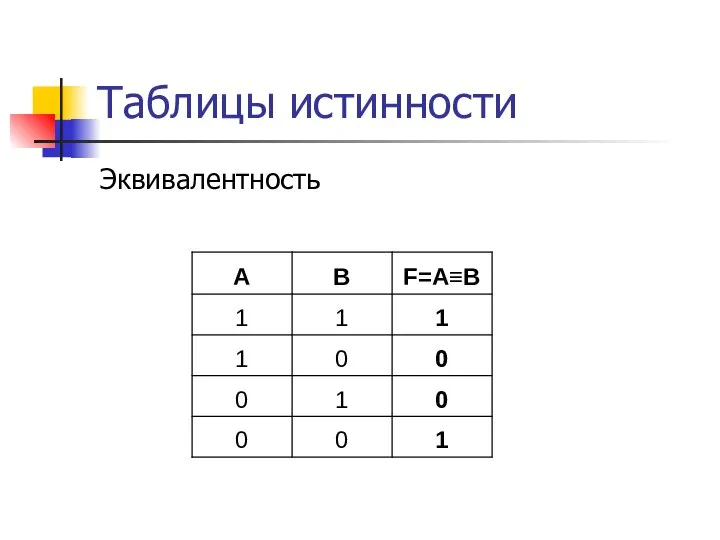
Таблицы истинности
Эквивалентность

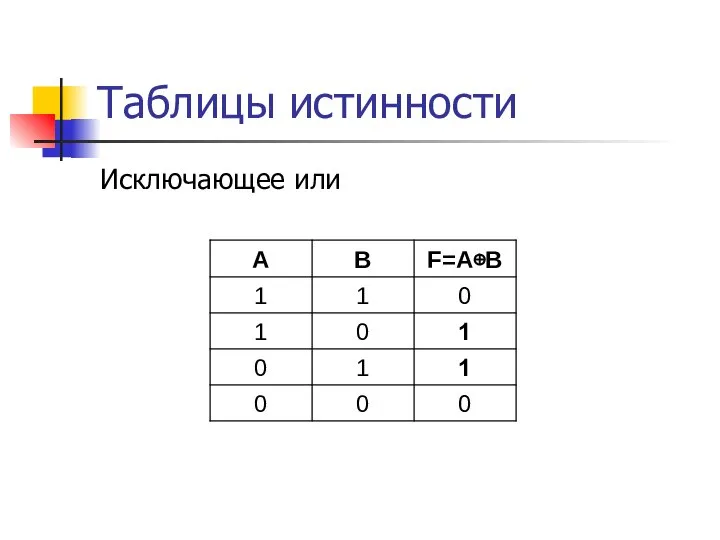
Таблицы истинности
Исключающее или

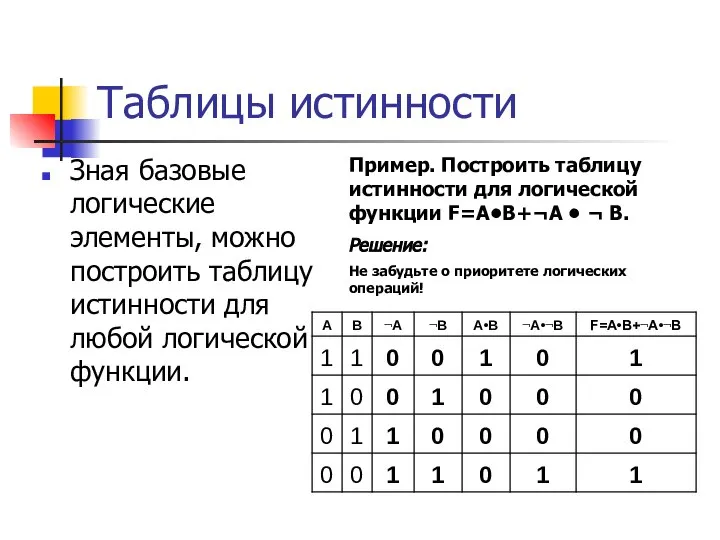
Таблицы истинности
Зная базовые логические элементы, можно построить таблицу истинности для любой логической функции.
Пример. Построить таблицу истинности для логической функции F=A•B+¬A • ¬ B.
Решение:
Не забудьте о приоритете логических операций!

Законы логики
1. Закон коммутативности
X•Y=Y•X
X+Y=Y+X
2. Закон ассоциативности
(X•Y)•Z=X•(Y•Z)
(X+Y)+Z=X+(Y+Z)

Законы логики
3. Законы поглощения (нуля и единицы)
X+0=X
X•1=X
4. Законы дистрибутивности
X •(Y+Z)=(X •Y)+(X •Z)
X +(Y • Z)=(X +Y) • (X +Z)

Законы логики
5. Закон противоречия
X •X=0
6. Закон исключенного третьего
X+X=1
7. Закон идемпотентности
X •X=X
X+X=X

Законы логики
8. Закон двойного отрицания
X=X
9. Законы де Моргана
X•Y=X+Y
X+Y=X • Y
10. Законы поглощения
X+X • Y=X
X •(X+Y)=X

Литература
Е.В. Андреева и др. «Математические основы информатики»
гл. 1.6