плотность вероятности p(x). Также определён алфавит квантователя и метрика искажения Будем называть минимальное число бит на один отсчёт, достаточное для представления значений X алфавитом с искажением, не превосходящим D, эпсилон-энтропией (функцией скорость-искажение - rate distortion function), R(D), и определять её так:
Понятно, что чем больше допустимое искажение D, тем меньше R(D) и наоборот.
Значение эпсилон-энтропии зависит как от статистики источника p(x), так и от метрики искажения Возможность получения результата в замкнутой форме – редкость.
Третья теорема Шеннона (кодирование источника с ограничением искажения, 1959)
Для источника без памяти, описываемого случайной величиной X, может быть выполнено кодирование со скоростью R и искажением D, только, если R > R(D). Для любого кода, обеспечивающего скорость R < R(D), искажение превышает D.
Иначе говоря, эпсилон-энтропия является нижней границей скорости кодирования при заданном уровне искажения (ошибки аппроксимации).
6.4.2. ЭПСИЛОН-ЭНТРОПИЯ (ФУНКЦИЯ СКОРОСТЬ-ИСКАЖЕНИЕ)












 Работу выполнил Пестов Григорий Работу выполнил Пестов Григорий ученик 9г класса МОУ СОШ с УИОП пгт. Ленинское Учитель Е.И.
Работу выполнил Пестов Григорий Работу выполнил Пестов Григорий ученик 9г класса МОУ СОШ с УИОП пгт. Ленинское Учитель Е.И.  Маленькая сказка о компьютерном вирусе и как с ним бороться
Маленькая сказка о компьютерном вирусе и как с ним бороться Инструмент для НТ Gatling
Инструмент для НТ Gatling Темы для самостоятельной работы. Развитие интернет технологий
Темы для самостоятельной работы. Развитие интернет технологий Преобразование форматов данных
Преобразование форматов данных Организация проведения и проверки в 2020/2021 учебном году контрольной работы для обучающихся 9 классов по информатике
Организация проведения и проверки в 2020/2021 учебном году контрольной работы для обучающихся 9 классов по информатике Повышение надёжности функционирования корпоративной телекоммуникационной сети
Повышение надёжности функционирования корпоративной телекоммуникационной сети Страшилка 2021
Страшилка 2021 QR - коды для игр
QR - коды для игр Основные понятия теории ИНС. Лекция № 8
Основные понятия теории ИНС. Лекция № 8 Презентация на тему Паскаль
Презентация на тему Паскаль  algebra_logiki
algebra_logiki Средства PHP для работы с MySQL
Средства PHP для работы с MySQL Компьютерные сети. Основные понятия
Компьютерные сети. Основные понятия В мире кодов. Способы кодирования информации. Метод координат
В мире кодов. Способы кодирования информации. Метод координат Компьютерные шрифты. Отрисовка. Форматы. Требования
Компьютерные шрифты. Отрисовка. Форматы. Требования Формализация и моделирование
Формализация и моделирование СЕТИ ЛЕК 4 СТ (Выч.маш) - копия - копия - копия - копия - копия - копия (2) (1)
СЕТИ ЛЕК 4 СТ (Выч.маш) - копия - копия - копия - копия - копия - копия (2) (1) Короткая инструкция по использованию мессенджера Gem4me. Все гениальное просто
Короткая инструкция по использованию мессенджера Gem4me. Все гениальное просто Презентація 5 клас Урок 7
Презентація 5 клас Урок 7 Актуальные способы мошенничества и защита от них
Актуальные способы мошенничества и защита от них Большие данные – это…
Большие данные – это… Экзаменационное задание по ПМ.03
Экзаменационное задание по ПМ.03 Проектирование цифрового компаратора
Проектирование цифрового компаратора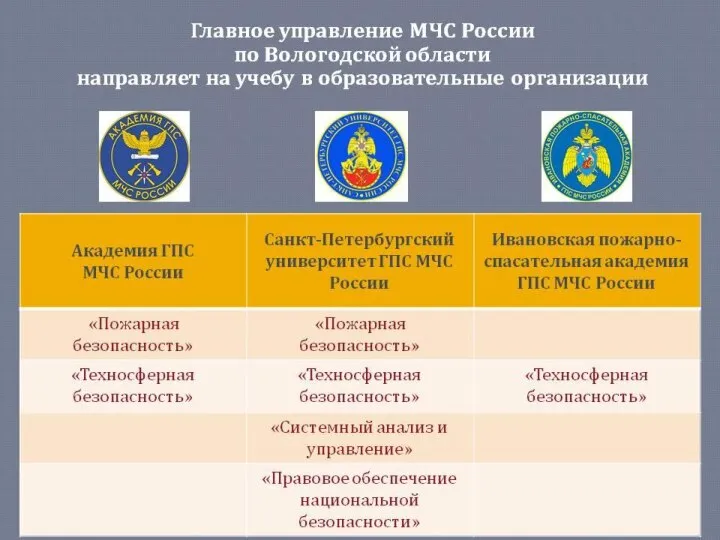 Вузы, специальности для онлайн урока
Вузы, специальности для онлайн урока Эволюция ОС
Эволюция ОС Проблемы надёжности и безопасности хранения и передачи информации
Проблемы надёжности и безопасности хранения и передачи информации Практическая работа 1. Знакомство Windows 7
Практическая работа 1. Знакомство Windows 7