Содержание
- 2. а) Рассмотрим, например, следующую спецификацию модели – регрессию логарифма цены на константу, число комнат, жилую площадь,
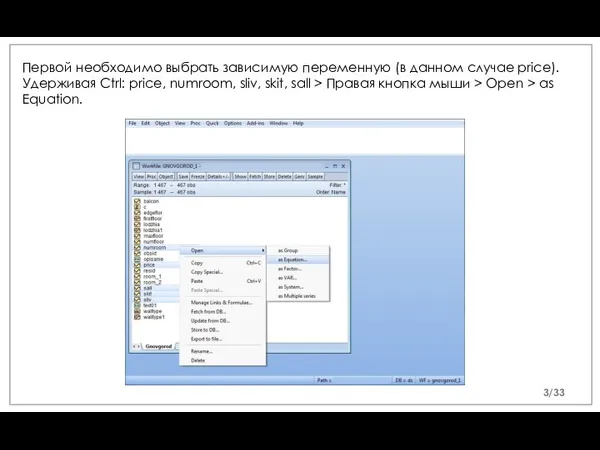
- 3. Первой необходимо выбрать зависимую переменную (в данном случае price). Удерживая Ctrl: price, numroom, sliv, skit, sall
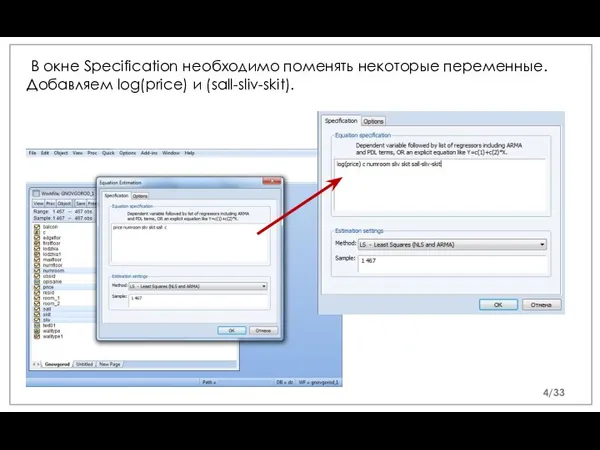
- 4. В окне Specification необходимо поменять некоторые переменные. Добавляем log(price) и (sall-sliv-skit). /33
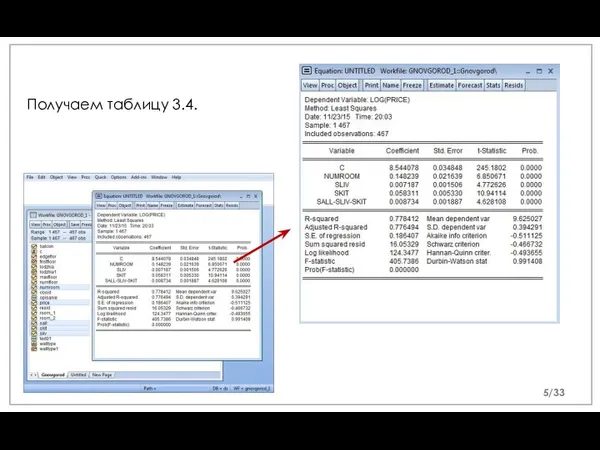
- 5. Получаем таблицу 3.4. /33
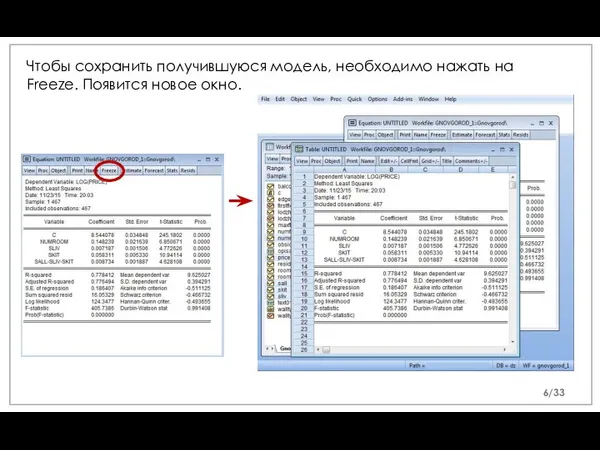
- 6. Чтобы сохранить получившуюся модель, необходимо нажать на Freeze. Появится новое окно. /33
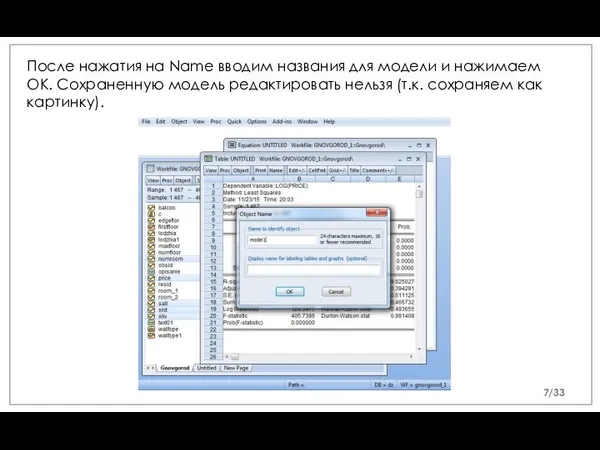
- 7. После нажатия на Name вводим названия для модели и нажимаем OK. Сохраненную модель редактировать нельзя (т.к.
- 8. Обозначим (price) начальную цену - P0, цену после добавления комнаты - P1. При добавлении одной комнаты
- 9. /33
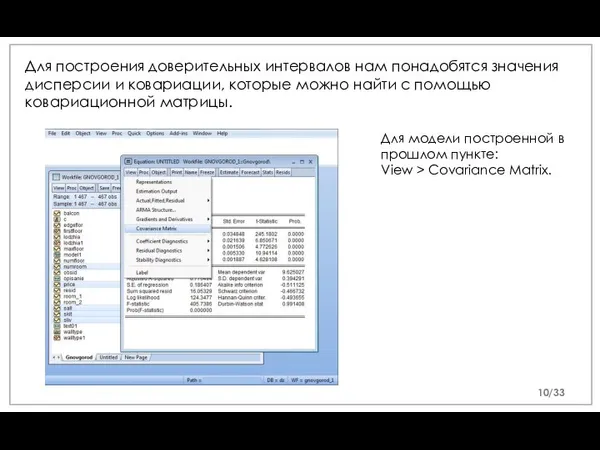
- 10. Для построения доверительных интервалов нам понадобятся значения дисперсии и ковариации, которые можно найти с помощью ковариационной
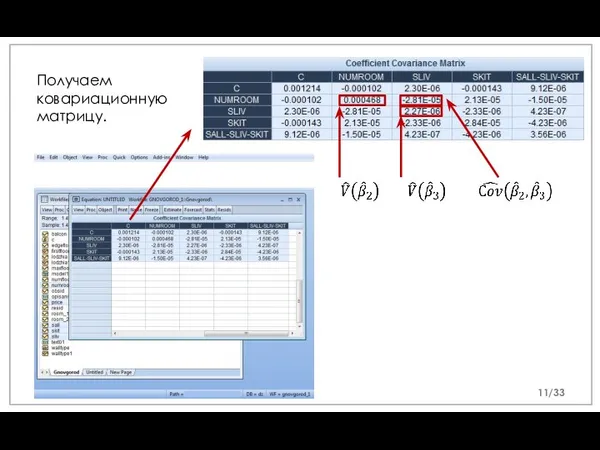
- 11. Получаем ковариационную матрицу. /33
- 12. Свойства дисперсии: Обозначим дисперсию (D) как VAR (V). /33
- 13. При добавлении 1 комнаты площадью 18 м2 цена с вероятностью 95% вырастет от 28,5% до 35,6%.
- 14. /33
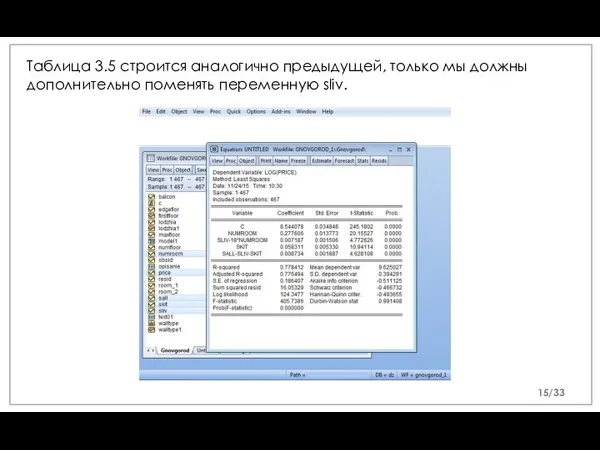
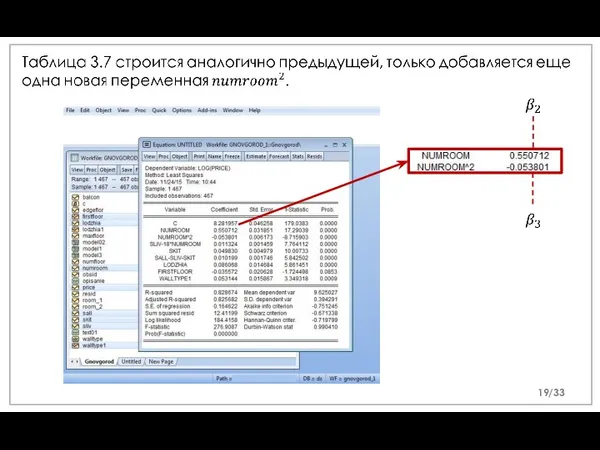
- 15. Таблица 3.5 строится аналогично предыдущей, только мы должны дополнительно поменять переменную sliv. /33
- 16. в) Попробуем включить в модель другие доступные параметры, от которых зависит цена квартиры. Это может не
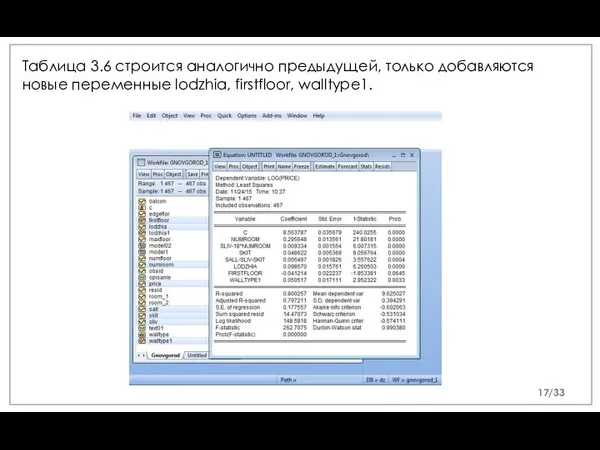
- 17. Таблица 3.6 строится аналогично предыдущей, только добавляются новые переменные lodzhia, firstfloor, walltype1. /33
- 18. /33
- 19. /33
- 20. Обозначим (price) начальную цену - P0, цену после добавления комнаты - P1. При добавлении одной комнаты
- 21. /33
- 22. /33
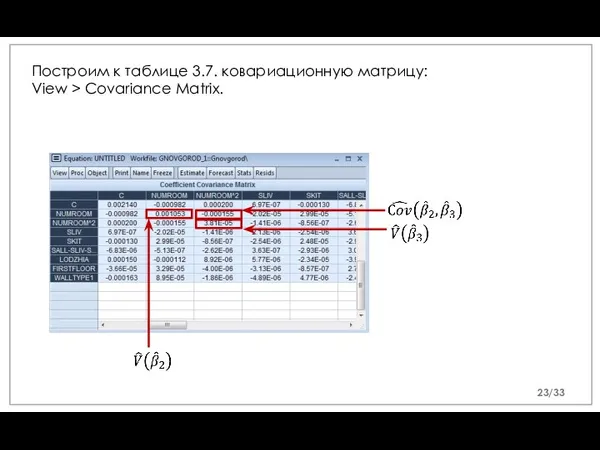
- 23. Построим к таблице 3.7. ковариационную матрицу: View > Covariance Matrix. /33
- 24. Построение доверительных интервалов При numroom=1: При добавлении 1 комнаты площадью 18 м2 к однокомнатной квартире цена
- 25. При добавлении 1 комнаты площадью 18 м2 к двухкомнатной квартире цена с вероятностью 95% вырастет от
- 26. При добавлении 1 комнаты площадью 18 м2 к трехкомнатной квартире цена с вероятностью 95% вырастет от
- 27. /33
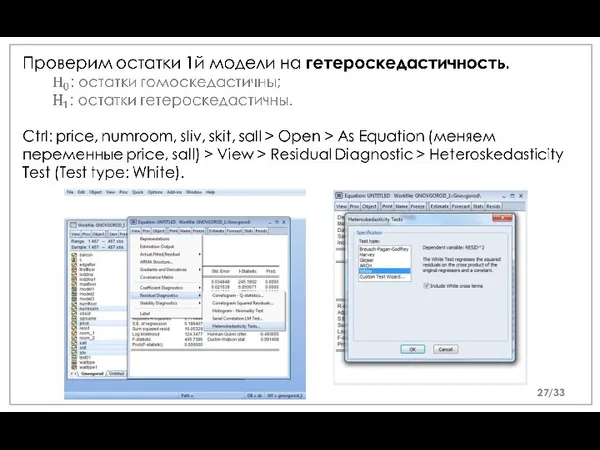
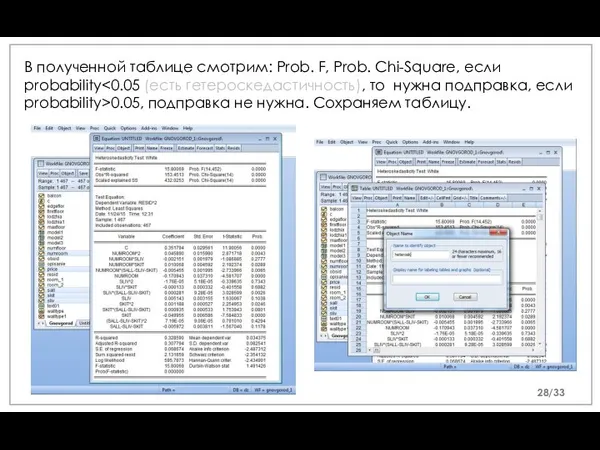
- 28. В полученной таблице смотрим: Prob. F, Prob. Chi-Square, если probability 0.05, подправка не нужна. Сохраняем таблицу.
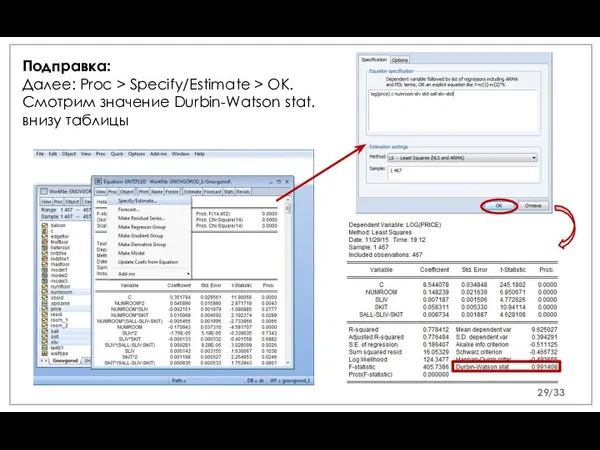
- 29. Подправка: Далее: Proc > Specify/Estimate > OK. Смотрим значение Durbin-Watson stat. внизу таблицы /33
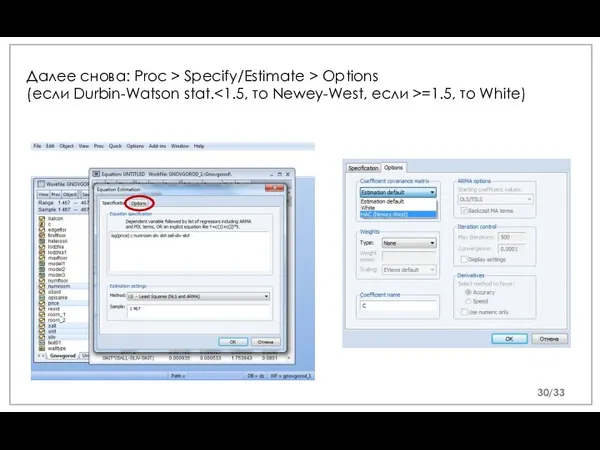
- 30. Далее снова: Proc > Specify/Estimate > Options (если Durbin-Watson stat. =1.5, то White) /33
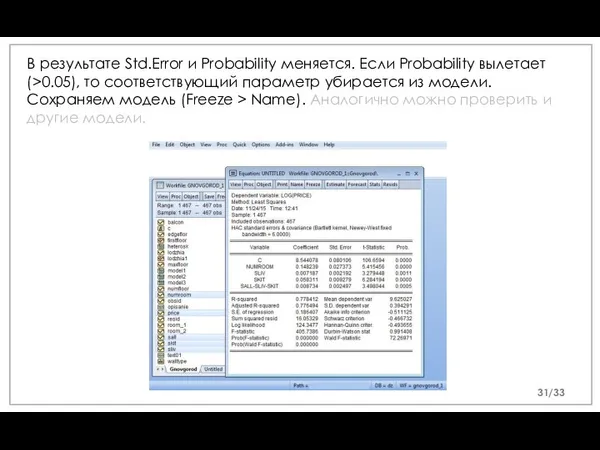
- 31. В результате Std.Error и Probability меняется. Если Probability вылетает (>0.05), то соответствующий параметр убирается из модели.
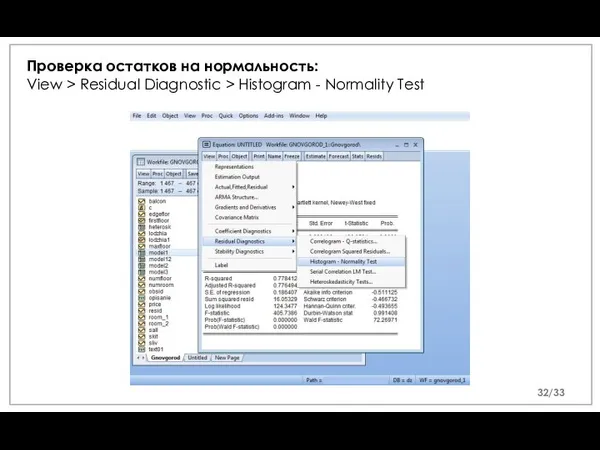
- 32. Проверка остатков на нормальность: View > Residual Diagnostic > Histogram - Normality Test /33
- 34. Скачать презентацию














 Dwed talent
Dwed talent 531642
531642 Хранение информационных объектов различных видов на разных цифровых носителях. Определение объемов различных носителей
Хранение информационных объектов различных видов на разных цифровых носителях. Определение объемов различных носителей Оценка количественных параметров текстовых документов
Оценка количественных параметров текстовых документов Система управления базами данных. 9 класс
Система управления базами данных. 9 класс Проблема идентификации пользователей сети Интернет
Проблема идентификации пользователей сети Интернет Сервис “Рука помощи” на официальном сайте Череповца
Сервис “Рука помощи” на официальном сайте Череповца Знакомство с языком HTML
Знакомство с языком HTML Моделирование пружин в прикладной библиотеке КОМПАС
Моделирование пружин в прикладной библиотеке КОМПАС История колдуна
История колдуна word
word Umbrella Security Service. Информационный комплекс 1.0
Umbrella Security Service. Информационный комплекс 1.0 Лекция 1 мат. пакет Matlab (1)
Лекция 1 мат. пакет Matlab (1) Ustroystvo_kompyutera_i_periferiynoe_oborudovanie
Ustroystvo_kompyutera_i_periferiynoe_oborudovanie Cервис Google Meet для проведения видеоконференций
Cервис Google Meet для проведения видеоконференций Специализация Data Science in Python
Специализация Data Science in Python Новий INVASION REVOLT RS
Новий INVASION REVOLT RS Python-Массивы (списки)
Python-Массивы (списки) Никнеймы. Что они могут рассказать о человеке?
Никнеймы. Что они могут рассказать о человеке? Интернет - банк данных о человеке
Интернет - банк данных о человеке Киберпреступность и киберпреступления
Киберпреступность и киберпреступления Тема_2. базовые средства
Тема_2. базовые средства Танковый биатлон
Танковый биатлон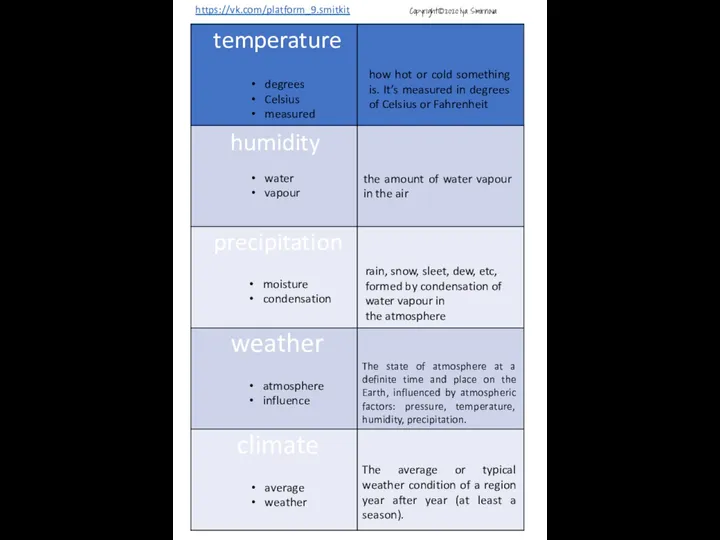 Weather definitions
Weather definitions Системы программирования и прикладное программное обеспечение
Системы программирования и прикладное программное обеспечение Ссылки – теория
Ссылки – теория WordPress 6-7
WordPress 6-7 Алгоритмизация и программирование. Язык C++
Алгоритмизация и программирование. Язык C++