08.09

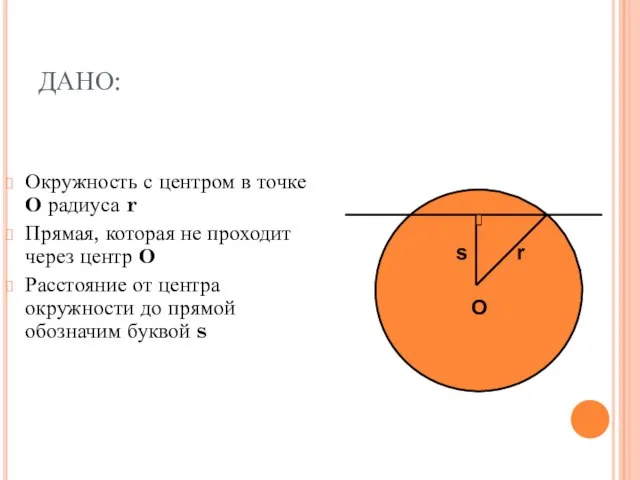
ДАНО:
Окружность с центром в точке О радиуса r
Прямая, которая не проходит через центр О
Расстояние от центра окружности до прямой обозначим буквой s
O
r
s

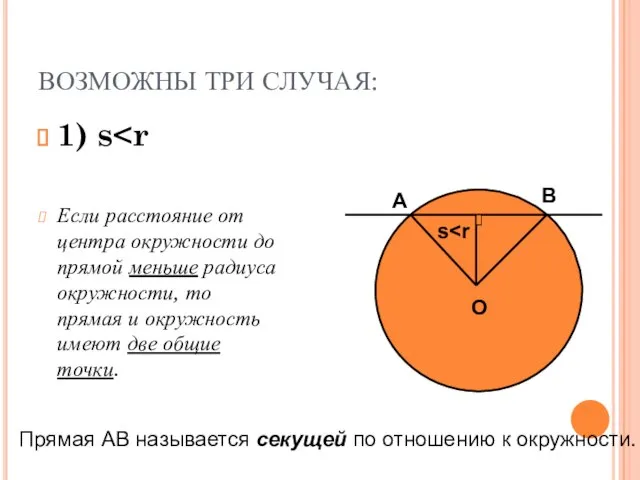
ВОЗМОЖНЫ ТРИ СЛУЧАЯ:
1) s
Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность имеют две общие точки.
O
s
А
В
Прямая АВ называется секущей по отношению к окружности.

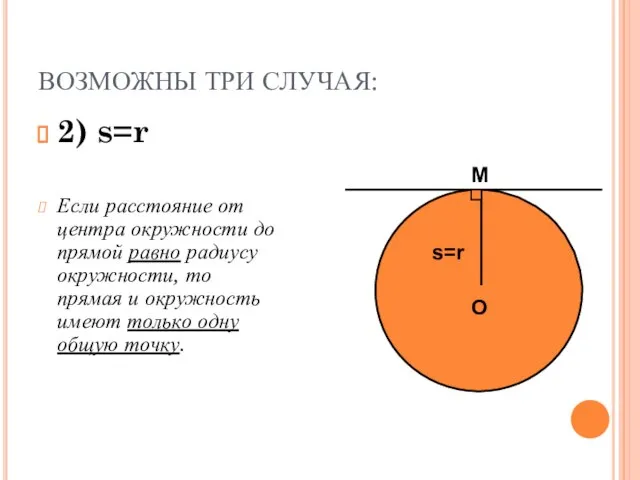
ВОЗМОЖНЫ ТРИ СЛУЧАЯ:
2) s=r
Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют только одну общую точку.
O
s=r
M

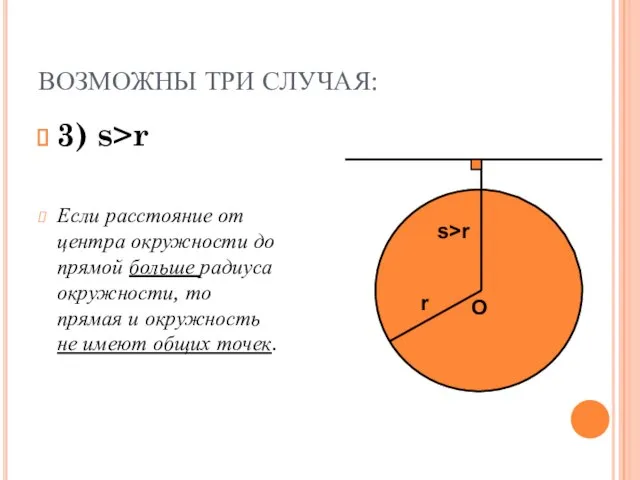
ВОЗМОЖНЫ ТРИ СЛУЧАЯ:
3) s>r
Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек.
O
s>r
r

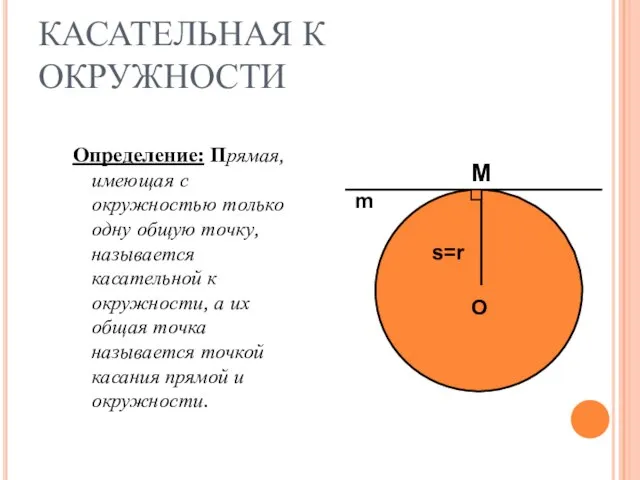
КАСАТЕЛЬНАЯ К ОКРУЖНОСТИ
Определение: Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.
O
s=r
M
m

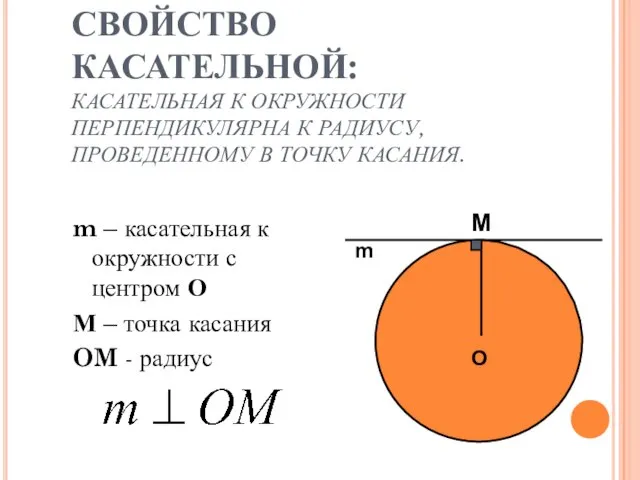
СВОЙСТВО КАСАТЕЛЬНОЙ:
КАСАТЕЛЬНАЯ К ОКРУЖНОСТИ ПЕРПЕНДИКУЛЯРНА К РАДИУСУ, ПРОВЕДЕННОМУ В ТОЧКУ КАСАНИЯ.
m – касательная к окружности с центром О
М – точка касания
OM - радиус
O
M
m

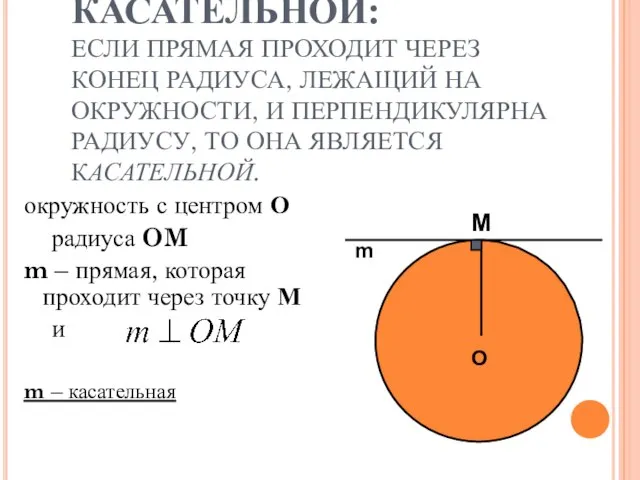
ПРИЗНАК КАСАТЕЛЬНОЙ:
ЕСЛИ ПРЯМАЯ ПРОХОДИТ ЧЕРЕЗ КОНЕЦ РАДИУСА, ЛЕЖАЩИЙ НА ОКРУЖНОСТИ, И ПЕРПЕНДИКУЛЯРНА РАДИУСУ, ТО ОНА ЯВЛЯЕТСЯ КАСАТЕЛЬНОЙ.
окружность с центром О
радиуса OM
m – прямая, которая проходит через точку М
и
m – касательная
O
M
m

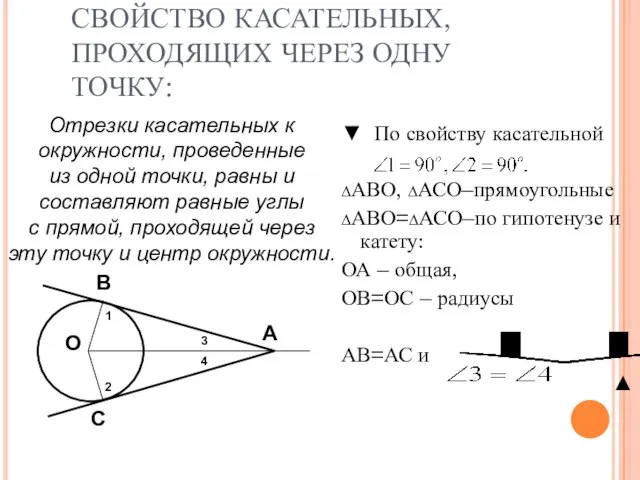
СВОЙСТВО КАСАТЕЛЬНЫХ, ПРОХОДЯЩИХ ЧЕРЕЗ ОДНУ ТОЧКУ:
▼ По свойству касательной
∆АВО, ∆АСО–прямоугольные
∆АВО=∆АСО–по гипотенузе и катету:
ОА – общая,
ОВ=ОС – радиусы
АВ=АС и
▲
О
В
С
А
1
2
3
4
Отрезки касательных к
окружности, проведенные
из одной точки, равны и
составляют равные углы
с прямой, проходящей через
эту точку и центр окружности.